一种复杂场景的局部实时规划决策与方法

杨朋举　周成平

(华中科技大学自动化学院多谱信息处理技术国家级重点实验室　武汉　430074)



一种复杂场景的局部实时规划决策与方法

杨朋举周成平

(华中科技大学自动化学院多谱信息处理技术国家级重点实验室武汉430074)

针对无人机改变飞行任务以及实际飞行航迹存在状态差异的问题,首先分析了不同的场景,同时指出与传统局部实时规划的差异,进而根据不同的场景进行决策与方法分析。最后,经过仿真实验验证,验证了方法的可行性与有效性。

局部实时; 状态差异; 改变任务; 场景; 决策方法

Class NumberV249

1　引言

信息化战争中,高空长航时无人机系统得到了各国空前的重视。迄今为止,无人机已经经历了伊拉克战争等六次的局部战争,充分显示了侦查、打击、空中战斗等方面的巨大作用[1]。

无人机导航需要较高的精度,同时需要一定的鲁棒性[3]。常用的导航方式中,惯性导航有隐蔽性好,实时性好等优点,但是也存在导航误差积累的问题;GPS有全天准确等优点,但是也有抗干扰性差等缺点;地磁导航可以利用地球固有资源导航,但是也存在导航精度低、变化磁场等问题;地形匹配导航具有不受电子干扰、全天候等优点,但是对地形的依赖性也很大。因此,以惯性导航为主,其他导航辅助匹配制导,往往会达到良好效果。无人机系统中,航迹规划具有很重要的作用。其中主要有以A*算法[11～12]为代表的确定性搜索方法和遗传算法[14]等为代表的不确定性搜索算法,并且已经应用于实践中。

局部实时规划领域,Qingbao Zhu[10]、Changwen Zheng[9]等研究了各种不同环境下的实时规划,但是规划的起点与结束点往往是确定并且已知的。T. Ishida[2]、郑昌文[4]等研究了目标变化的实时规划,但是起始点是确定的并且类似于一边规划一边飞行的情况,并且大都默认为向着轨迹的前方飞行。现在面临的情况是起始点与结束点都是动态未知,并且有复杂的场景变化,不同于以前的局部实时规划。表现为:1)无人机实际飞行时,局部范围内出现新的任务,并且后续的原有任务不再执行,执行完新任务可能还需回到侦查飞行起点的情况;2)实际飞行时,原有的匹配区无法完成正确匹配校正的的情况。当然无人机实际飞行时可能碰到多种情况,现在只针对以上两种情况,进行场景分析,进而在局部范围内进行决策与方法分析,完成实时调整。

2　两种具体问题的介绍

2.1匹配区的匹配失败

预规划的航迹采用导航点链的形式进行存储,导航点形式有起始点,直飞段(两个端点),弧线段(转弯起始点,转弯中心点,转弯结束点),匹配区(具有宽度与方向的匹配区,简化为中心匹配点),任务区(简化为中心任务点)构成。

在预规划的任务链上存在很多匹配区,在每个匹配区处进行辅助匹配校正,减小惯导误差。如图1,但是实际飞行的过程中,存在某个匹配区无法进行匹配的情况。一旦匹配区无法辅助匹配校正,无人机就可能沿着误差曲线漂移的越来越远,无法完成后续的飞行任务。为了改变这种状况,需要在匹配失败信息出现时,以失败匹配点所在位置选定局部区域,进而在所在场景内确定局部规划起点与结束点,进行局部实时调整,不影响后续的任务执行。出现匹配失败时,多是结束点在原规划航迹前方的情况,分别采用A*算法,改进稀疏A*算法,遗传算法进行实现,分析几种算法在此场景中的适应性。

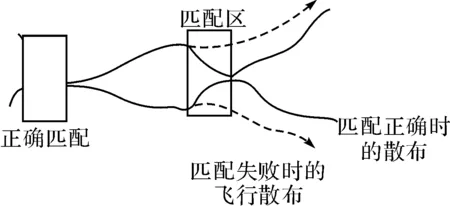
图1　匹配区匹配失败示意图

2.2任务改变的情况

如图2,无人机从最初的起飞点Fs开始飞行,飞到当前位置S,突然需要改变任务。具体分为两种:第一,出现新的任务区N,但是后面的任务不再执行,执行过程就是S—N的规划;第二,在新任务N执行后,需要回到无人机的最起始位置Fs,当然过程中可能需要添加许多临时规划点Pi,执行过程就是S—N—P1—P2…Pi…Fs。这两种情况,预规划的航迹与任务都不再满足,需规划新的轨迹。对于规划方向差异过大的情况,杨杰[13]提出了在任务点周围反向规划设置引导点的决策,宋文兵[15]等也提出有向圆的思想在任务添加时解决规划距离过近与规划方向差异过大的情况,但是跟本文的场景都存在一定的差异。

经过分析,在有向圆思想解决位置关系与方向关系问题的基础上,进一步探讨有向圆在任务改变中的应用。同时对于有向圆的定义与位置关系如何分类进行简化处理与实现,对于任务改变需要回到原始起点的复杂场景进行分析与决策,对于多次规划中临时结束点可能陷入禁飞区的情况进行处理,同时对于不同的场景实现连续模拟与局部调整,使得场景模拟更加接近真实场景,仿真实验更加方便快捷。

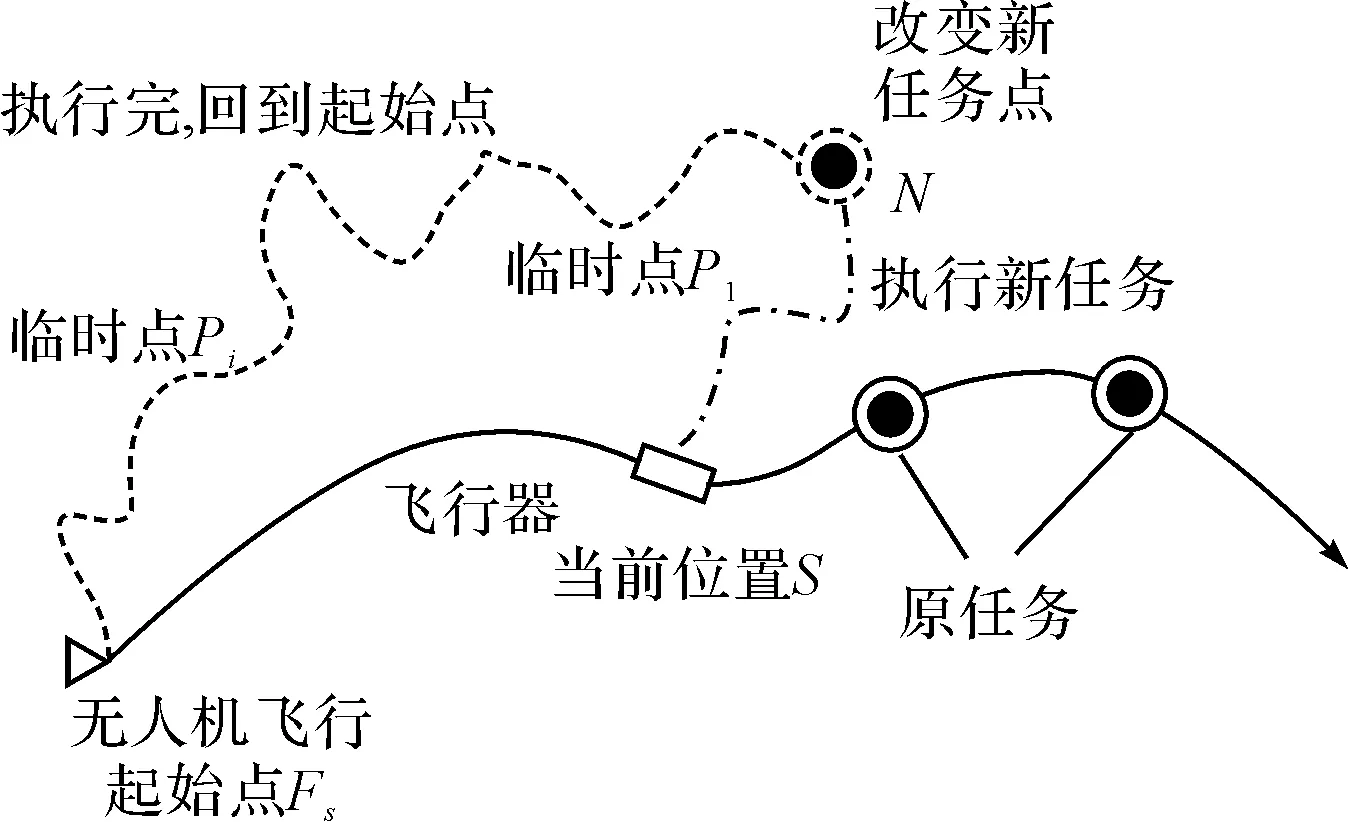
图2　无人机改变任务示意图

3　局部实时规划的规划决策与方法

3.1约束条件

1) 机动约束:最大爬升角度/俯冲角度,最大爬升距离/下降距离,最小转弯半径,无人机最大转弯角度等;

2) 环境约束:地形、战术、气象等禁飞区与威胁区的约束,匹配区的选择与方向约束,规划需要的时间,规划航迹的航程等。

3.2匹配失败

3.2.1场景分析

无人机实际飞行时,预规划航迹上有很多匹配区来进行匹配,以校正惯性导航的时间积累误差。但是实际飞行时,可能出现某种状况,使得无人机无法进行匹配区校正。此时,需要确定调整起点、局部区域、调整结束点进行局部实时的调整。匹配失败的匹配区的出区位置作为调整起点,根据调整起点为中心确定局部调整区域。对于可能出现各种导航点与匹配区、任务区组合出现的复杂场景进行简化处理,把局部区域内是否存在任务点来作为不同场景的唯一分类标准,场景图如图3,具体过程如下:

1) 在局部调整区域内的所在航迹上,若存在任务点,此时可以把最近的任务点T作为局部调整的调整结束点;

2) 若在局部调整区域内的所在航迹上,搜索不存在任务点,此时可以把原规划航迹与局部局域的边界的相交点C作为调整结束点;

其中调整结束点的确定特别重要,求调整结束点的步骤为(1)确定匹配失败情况的起点S;

(2)以起始点作为中心点,确定具体的矩形调整区域;

(3)在矩形区域内搜索原航迹的向前导航点,如果存在任务点T,则把最近任务点作为局部调整结束点,否则转下一步;

(4)搜索到原航迹与局部区域相交的前后两个导航点A与B,如果是直线段,直接求直线段与四条边界线段交点作为调整结束点;否则是弧段,则采用二分法求得弧线段与边界的交点,作为调整结束点。

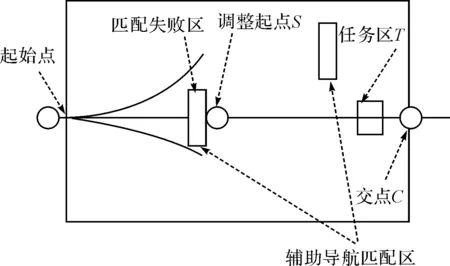
图3　匹配失败某种场景示意图

3.2.2方法分析

1) A*算法是一种常用的确定性航迹搜索算法。优点是针对具体场景,若设计合适,能较好地完成航迹规划,找到最优解或者近似最优解,且解能重复;缺点是搜索时间不能确定,因为A*算法是基于遍历收敛的。但是传统的A*算法容易出现组合爆炸的问题,不满足局部实时规划。Robert J[5,8]关于稀疏A*算法的提出,减少了搜索的区域,也可以得到最优或者次优的结果。

根据传统的三维规划A*算法出现的问题,本文在匹配失败具体场景中运用几种策略,改进A*算法:(1)采用稀疏A*算法,在一定的角度内进行变步长搜索,代替全空间遍历;(2)三维高度规划过程中,采用先平面规划,选择合适的平面规划路径再进行高度规划;(3)对于匹配区地图,把地图稀疏化,不同的分辨率进行搜索,先低分辨率大区域搜索,搜索不到则减小区域增大分辨率搜索,直到搜索到合适的匹配区。

2) 遗传算法是一种随机性的搜索方法。通过交叉、变异、选择复制几种基本算子,从而具有强大的搜索能力,可找到次优解或者满意解[14]。现在遗传算法在航迹规划中,已是一种比较成熟的算法,同时要考虑航迹如何编码以及代价函数的设置。在本文中,航迹个体采用导航点链来表示,同时任务区和辅助匹配区也可以由中心点代替表示。航迹代价同时有几部分构成,有机动代价、威胁区禁飞区代价、航迹长度代价,同时代价与各项约束有很大的关系。

3) 优化指标

(1)可行解:要搜索到满足各种约束并且总体适合的航迹,应该得到可行解或者次优解;

(2)时间合理:对于匹配失败的局部实时航迹规划,对于时间的要求还是比较高的,满足实时性的要求;

(3)成功率高:对于规划时间一定的情况下,成功率的高低也直接影响了整体的规划效果。

3.2.3实验结果与分析

本实验的编程环境为Visual Studio 2005与Qt4.6.3,运行在Intel双核 E7400、2.8GHz处理器,内存为2.0G,系统为WIN7 32位机系统,实验地图分辨率为100m×100m,局部环境是以当前点为中心的上下前后各100km范围内。

匹配失败的场景,随机选取不同航迹的不同的匹配失败点,分为A*算法,改进稀疏A*算法(如图4)与遗传算法(如图5)进行实验,图6是高度规划图,统计了四条航迹的56个匹配失败点,记录数据如表1所示。

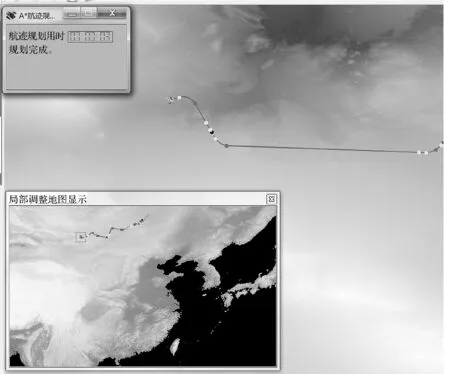
图4　改进稀疏A*算法规划结果

不同算法平均时间(s)最长时间(s)处理成功率A*算法39.015978.6%改进稀疏A*算法3.4998.2%遗传算法2.2793%

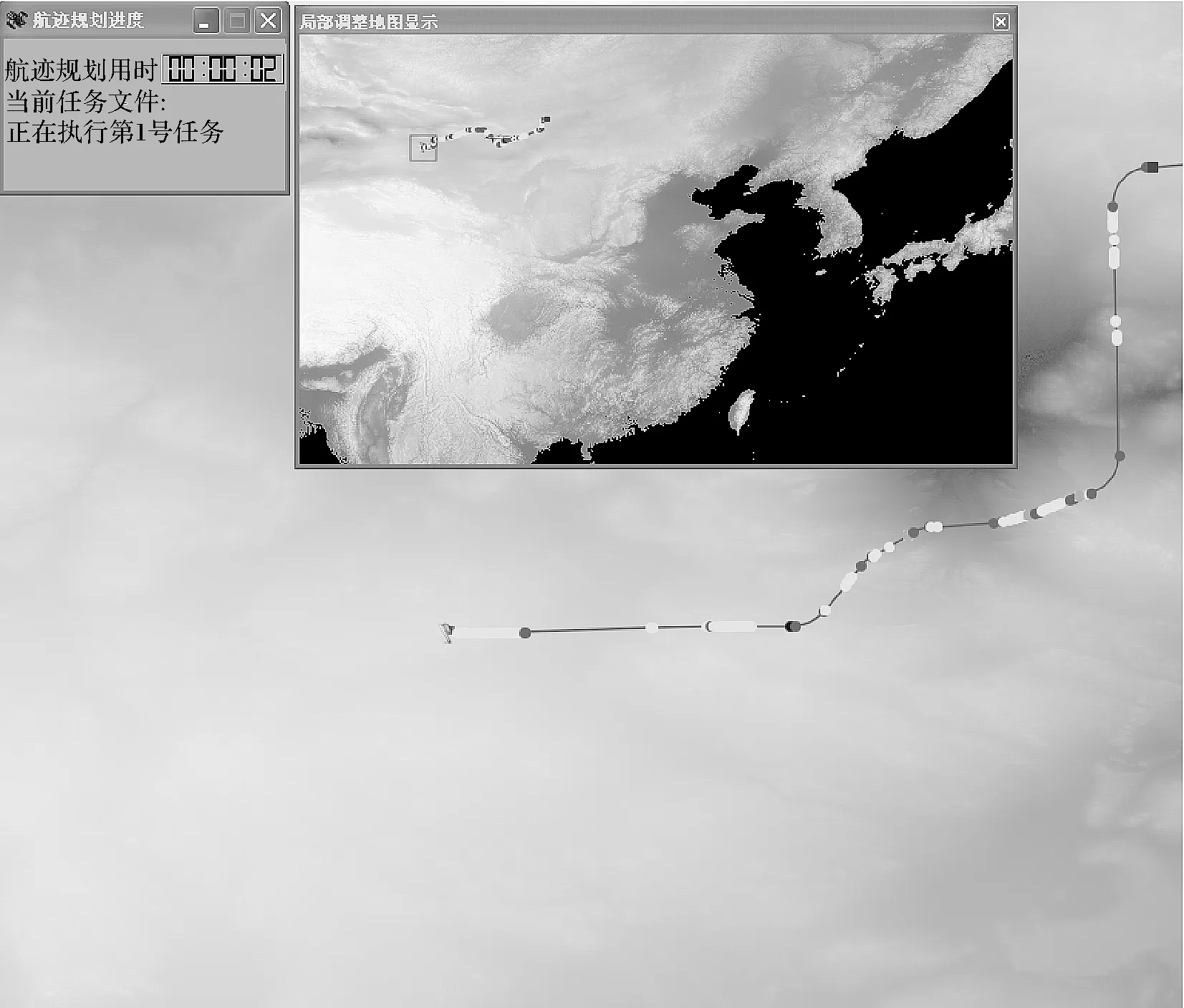
图5　遗传算法的匹配失败规划结果

图6　高度规划规划结果

通过实验结果可知,传统A*算法平均时间较长,处理成功率也比较低。改进的稀疏A*算法搜索的效率与时间明显高于一般A*算法,同时基于遍历的原理也使改进稀疏A*算法的时间稍长于遗传算法,但是成功率也略高。因此,对于匹配失败的情况,改进的稀疏A*算法与遗传算法都能满足规划时间小于10s的高成功率的实时规划要求,相比之下,遗传算法在规划时间上稍有优势,改进的稀疏A*算法在规划成功率上稍有优势。

3.3任务改变

3.3.1场景分析

无人机实际飞行中,突然接到新的任务命令,并且旧的任务不再执行。有不同的情况,第一是执行完新任务就结束,第二是执行完任务需要回到原始起飞点。新任务执行时,考虑到新任务的距离和方向的多变性,例如起点与结束点的方向偏差比较大的情况,或者起点与结束点的距离过近时,可通过改进的有方向圆来处理这个问题。对于不需要回到起点的情况,确定好规划起点与结束点,局部区域,采用有向圆算法进行航迹规划。

1) 起点:出现新任务的时刻,无人机所在点作为起始点;

2) 局部区域:以起始点为中心,建立矩形区域作为局部调整区域;

3) 结束点:新任务点作为调整结束点。

对需要回到起始点的情况,可能需要较长时间,采用选定临时规划点,多次局部规划的办法,具体操作步骤为

1) 出现新任务时刻的无人机所在位置作为调整起始点;

2) 新任务所在位置作为临时调整结束点,并且调用第一种情况下的算法进行局部调整,转下一步;

3) 检测整条航迹的原始起始点是否在规划区域内,如果在,则把更改任务作为起始点,原始起点作为结束点进行规划,规划结束;否则转下一步;

4) 原始起点不在规划区域内,则把前一次的规划结束点作为本次规划起始点,本次规划起始点与任务链起始点的连线与局部边界的交点作为本次规划的结束点;

5) 最终每一段都规划成功,则连接回到原始起点的多段规划航迹,但是此时可能要多次局部规划,就需要比较长的时间,因此这种情况的主要衡量指标为任务执行的成功率,多段执行成功回到起始点。

3.3.2方法分析

对于改变任务的出现的位置与方向的多样性,复杂的场景构成,回到原始起点时生成的临时规划点可能落入禁飞区的情况,准备在有向圆的有关概念的基础上进一步改进并且应用于改变任务中。

1) 有向圆定义与可行公切线概念介绍

在初等数学上平面圆有如下概念:在一个平面内,线段OB绕它固定的一个端点O旋转一周,另一个端点B旋转生成的图形叫做圆[6]。我们约定,在一个平面内线段OB绕它的圆心旋转时,有顺时针和逆时针的两个旋转方向,顺时针旋转生成的圆叫做顺时针圆,逆时针旋转生成的圆叫做逆时针圆,顺时针圆和逆时针圆合成有向圆。

假设有起点有向圆S与结束点有向圆T相离,则两圆有四条公切线,有且仅有一条合适公切线。合适公切线满足起点有向圆S与结束点有向圆T与公切线的方向一致。可以通过起始圆与目标圆的不同方向进行组合,有四种情况,每种情况都有且仅有一条合适公切线,再选择最优的公切线。

2) 两圆位置关系分类简化处理

常见的两圆的位置关系分为五种,分别为外离、相交、外切、内切、内含,针对不同的位置关系进行分别处理,十分繁琐[7]。为了进一步简化处理,如果假设起点圆为有向圆S,终点圆为有向圆T。有向圆对可以看做一个平面上的集合,w1(s(x,y)|x2+y2≤r2),w2(T(x,y)|x2+y2≤r2)。根据集合w1与集合W2交集是否为空,把两有向圆的位置关系简化为两种:第一种为两个集合无交集,即两个圆相离的情况,可以做四条公切线;第二种,是两个集合有交集,可能是除了外离之外的任何一个,此时没有必要进行细分,只需要在两个圆心的中垂线上选择合适的第三个点,再构造临时有向圆P,构成起点圆S与临时有向圆P、临时有向圆P与终点圆T的两对集合无交集的相离圆对。

3) 临时调整点落入禁飞区或者威胁区的处理

改变任务回到原始起点的过程,把新任务与规划原始起点的连线和局部边界的交点作为临时调整点,同时回到起始点的过程中也可能有多个临时调整点。但是临时调整点存在可能落入禁飞区的情况。这个情况跟匹配失败的过程不同,因为匹配失败过程选定的调整结束点都在预规划航迹上,满足禁飞区与威胁区的约束。因此具体处理如下:

(1)根据新任务与规划原始起点的连线和局部边界的交点作为临时调整点;

(2)检测临时调整结束点是否在禁飞区或者威胁区内;

(3)如果不在禁飞区或者威胁区内,则把临时调整点作为临时调整结束点;

(4)假若在相关区域,需要设置一定的角度与距离进行多次扰动,同时转2);

(5)如果扰动达到最大次数或者扰动后此点不在禁飞区或者威胁区内,转3)。

4) 有向圆解决方向偏差大与距离近的问题

本文采用有向圆,采用前后弧段无人机机动飞行,中间切线遗传算法规划的方法,可以有效地解决规划起点S到规划终点T方向偏差大的问题。如图7,前弧段S-M和后弧段N-T机动转弯飞行,切线段M-N进行遗传算法规划。

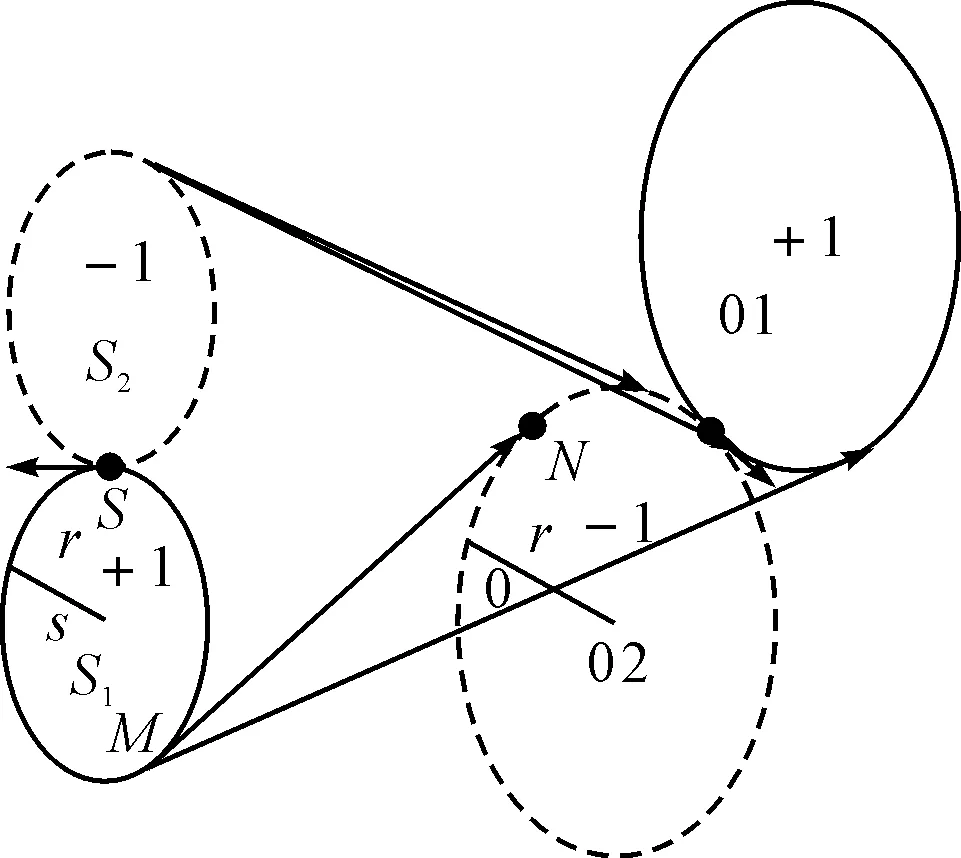
图7　方向偏差大的有向圆方法的示意图

两个圆之间有多种位置关系,如果相离,一定存在合适的满足方向的公切线,如果是非相离的距离过近的情况,都可以在两圆的中垂线上选择新任务点,进行两段规划即可,每一段都参照方向偏差大的具体过程。方向偏差大与距离过近的具体步骤如图8所示。

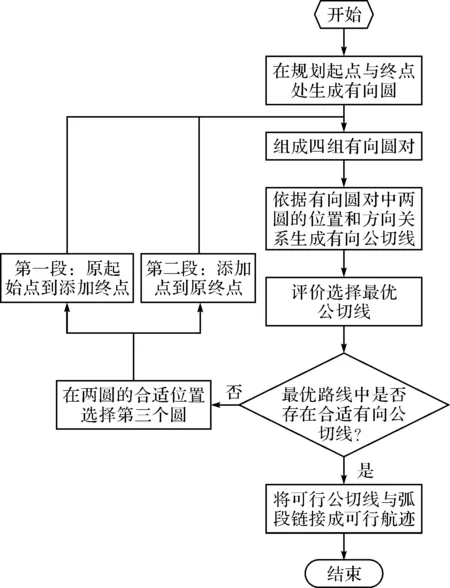
图8　方向偏差过大与距离过近的有向圆

处理流程图

5) 一条航迹实现多次模拟与局部调整

针对匹配失败与任务改变的情况,设计之初,是针对每一种情况进行单独处理,不利于连续多场景的演示与仿真,在保持各种情况的单独处理外,设置一个综合接口,使得规划方法能够对于复杂场景与不同情况进行连续模拟与处理,循环呈现。

3.3.3实验结果与分析

实验环境同3.2.3节,改变任务分为两种,一种是改变后回到起始点的实验如图9,另一种改变后结束,不需要回到起始点。采用改进的有向圆方法进行处理,选取四条航迹50次试验记录数据,统计结果如表2所示。

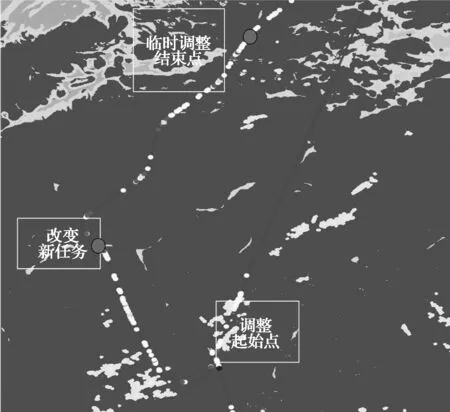
图9　任务改变回到起始点实验结果图

改变任务平均时间(s)最长时间处理成功率不回起始点1297.5%需回起始点XX95%

对于改变任务,容易出现规划起点与结束点方向差别大与距离过近的情况。实验验证,采用本文方法,不需要回到原始起点的任务改变的规划平均时间为1s,成功率高达97.5%;需要回到起始点的任务改变情况由于需要不断滑动窗口多次规划,规划时间跟与原始起点的距离有很大关系,同时本算法对于临时结束点可能陷入禁飞区的处理也使算法鲁棒性更高,有很高的处理成功率。

4　结语

本文针对无人机出现的匹配失败无法完成匹配的问题,经过改进的A*算法与遗传算法都能完成局部实时的规划。针对任务改变的情况,采用经过处理的有向圆的局部规划算法,很好地解决了改变任务回到起始点的问题。因此,本文对这两种问题的算法解决是可行的,同时对于多无人机的局部规划具有借鉴作用。

[1] 秦博,王蕾.无人机发展综述[J].飞航导弹,2008(8):2-5.

QIN Bo, WANG Lei. Unmanned aerial vehicle (uav) development review[J]. Journal of Maneuverable Missile,2008(8):2-5.

[2] T. Ishida, R. E. Korf. Moving-target search: a real-time search for changing goals[J]. IEEE Transaction on Pattern Analysis and Machine Intelligence,1995,17(6):609-69.

[3] 周姜滨,袁建平,罗建军,等.高空长航时无人机导航系统研究[J].西北工业大学学报,2008,26(11):463-466.

ZHOU Jiangbin, YUAN Jianping, LUO Jianjun, et al. High-altitude long-endurance uav navigation system research[J]. Journal of Northwestern Polytechnical University,2008,26(11):463-463.

[4] 郑昌文.飞行器航迹规划方法研究[D].武汉:华中科技大学,2003.

ZHENG Changwen. Research of UAV route planning method[D]. Wuhan: Huazhong University of Science and Technology,2003.

[5] Robert J Szczerba, Peggy Galkowski Ira S C lickstein, Noah Ternullo. Robust A lgorithm for A lgorithm for Real-time Route Planning[J]. IEEE Trans. on Aerospace and Elec-ronic System,2000,36(3):869-878.

[6] 李金明.二维文本条形码识别系统关键算法的设计及实现[D].广州:华南理工大学,2013:32.

LI Jinming. Two-dimensional bar code text recognition system design and realization of the key algorithm[D]. Guangzhou: South China University of Technology,2003:32.

[7] 章建跃.构建逻辑连贯的学习过程使学生学会思考[J].数学通报,2013,52(6):6-7.ZHANG Jianyue. Build the logic coherence of the learning process to make the students learn to think[J]. Bulletin des Sciences Mathematics,2013,52(6):6-7.

[8] Szczerba Robert J. Robust algorithm for real-time route planning[J]. IEEE Transactions on Aerospace and Electronic Systems,2000,36(3):869-878.

[9] Changwen Zheng, Mingyue Ding, Chengping Zhou. Real-time route planning for unmanned air vihicle with an evonutionary algorithm[J]. International Journal of Pattern Recognition and Artificial Intelligence,2003,17(1):63-81.

[10] hu, Jun Hu, Wenbin Cai, Larry Henschen. A new robot navigation algorithm for dynamic unknown environments based on dynamic path re-computation and an improved scout ant algorithm[J]. Applied Soft Computing,2011,11(8):4667-4676.

[11] Robert J S, Peggy G I S. Clickstein, Noah Ternul-lo. Robust algorithm for algorithm for real-time routeplanning[J]. IEEE Trans. on Aerospace and Electronic System,2000,36(3):869-878.

[12] 李春华,郑昌文,周成平,等.一种三维航迹快速搜索方法[J].宇航学报,2002,23(3):13-17.

LI Chunhua, ZHENG Changwen, ZHOU Chengping, et al. A three-dimensional track fast search method[J]. Acta Astronautica,2002,23(3):13-17.

[13] 杨杰.具有端点方向约束的快速航迹规划法研究[D].武汉:华中科技大学,2013.

YANG Jie. The fast route planning method to adapt to the directional endpoint constraints[D]. Wuhan: Huazhong University of Science and Technology,2013.

[14] 张铃,张钹.遗传算法机理的研究[J].软件学报,2000,11(7):945-952.

ZHANG Ling, ZHANG Bo. The researches on the mechanism of the genetic algorithm[J]. Journal of Software,2000,11(7):945-952.

[15] 宋文兵,周成平.一种基于超差信息的局部实时航迹规划方法[J].计算机与数字工程,2015(12):2159-2163.

SONG Wenbing, ZHOU Chengping. A Local real-time path Planning Method based on the flight error[J]. Computer & Digital Engineering,2015(12):2159-2163.

A Local Real-time Route Planning Decision and Method Based on Complex Scene
YANG PengjuZHOU Chengping
(National Key-Laboratory for Multi-Spectral Information Processing Technology,

School of Automation, Huazhong University of Science and Technology, Wuhan430074)

Aiming at the problems of changing the target point and the actual flight status different from original planning paths for the UAV(Unmanned Aerial Vehicle), this paper first analyzes the complicated scene and context, then introduces the differences from the traditional local real-time route planning. Furthermore ,according to the multifarious scene, a strategic decision is made and the corresponding algorithms are realized. Finally, through simulation experiment, the feasibility and effectiveness of the method is validated.

local real-time, status differences, changing target, scene and context, strategic decision

2016年2月4日,

2016年3月11日

杨朋举,男,硕士研究生,研究方向:任务规划,优化算法。周成平,男,副教授,研究方向:图像处理,任务规划,计算机视觉。

V249

10.3969/j.issn.1672-9722.2016.08.007