格点法模拟静电场电势分布
牛英煜,王 荣
(大连交通大学,辽宁 大连 116028)
格点法模拟静电场电势分布
牛英煜,王荣
(大连交通大学,辽宁 大连116028)
利用格点法模拟静电场在二维平面内的电势分布.具体描绘了点-点、点-线、线-线,以及同心圆环的静电场等势线分布情况,并与理论计算结果进行比较。同时还分析了同心圆环产生的电势与同轴圆柱面产生的电势的区别。
格点法; 电势; 点电荷; 线状电荷
电荷产生的静电场及电势分布是大学物理的基础内容。但由于静电场分布无法直接探测,因此实验上常用稳恒电流场来模拟描绘静电场电势分布。理论上,通常利用场强计算公式,通过积分求得电场解析式,利用该解析式描绘静电场分布[1,2]。
格点法是根据一定的数值方法,将连续的空间离散成有限的单元。该方法被广泛地用于力学、原子与分子物理、化学物理等方面[3,4]。本文利用格点法,将二维平面等间隔离散为10 000个点,利用公式
(1)
计算出每个点电荷在各格点产生的电势,再利用电势叠加原理,将各点电荷产生的电势叠加,从而得到各格点的电势分布。最后利用Origin软件,等间隔画出等势线。由于等势线的疏密与电场强度相关,因此根据等势线分布还能反映出场强分布情况。
1 点电荷电势分布
图1为利用格点法,并借助Origin作图软件描绘的点电荷电势分布图。图中的“+”号与“-”号分别代表点电荷的正负,每个点电荷所带电量都相同。从图1中可以看出,由于每两条邻近等势线间的电势差都是相等的,所以越靠近点电荷处,电势线分布越密。对于紧邻点电荷附近处的各格点,由于其位置与点电荷距离较小(r→0),这些格点位置所对应的电势远大于离点电荷相对较远的其它格点的电势。
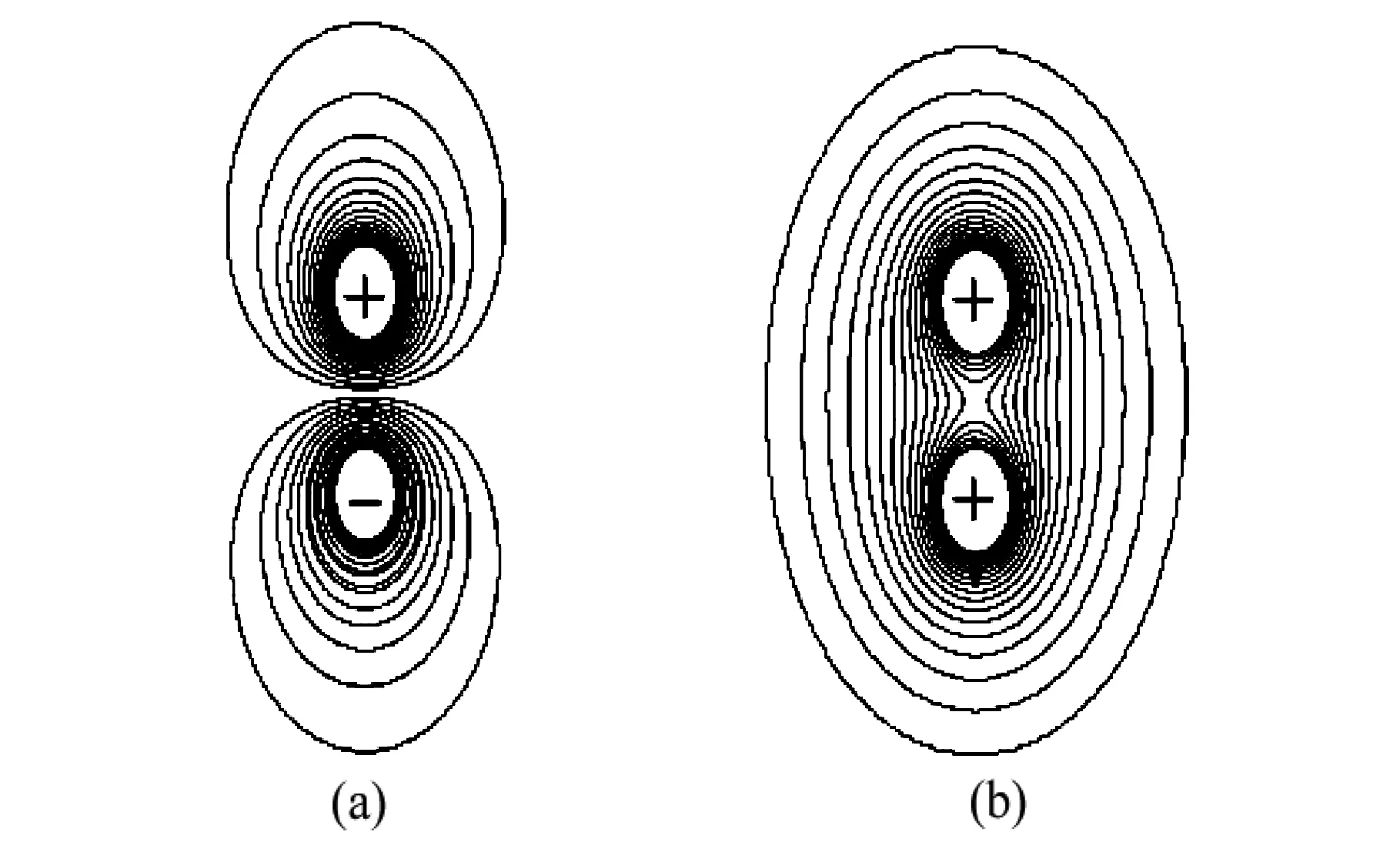
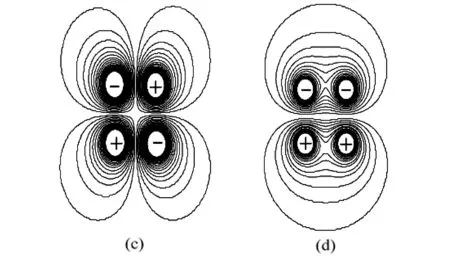

图1 点电荷等势线分布
因此紧邻点电荷附近处的电势线非常密集,电势线分布无法区分。本文没有描绘出紧邻点电荷附近的电势线分布。
图1分别描绘了2、4、5、8个点电荷的电势线分布情况。图1(c)中,当四个点电荷为“+-+-”分布时,虽然正电荷与负电荷产生的电势正负不同,但各点电荷产生的等势线形状相同,并呈对称分布。图1(d)中,当四个点电荷为“--++”分布时,两个正电荷与两个负电荷产生的电势线分为上下两个图形,每个图形的形状都与图1(b)相似;上下两个图形呈对称分布,其对称形状与图1(a)相似。也就是说,图1(d)同时具有图1(a)与图1(b)的特点。当五个点电荷呈直线分布时,其产生的等势线与图2中的直线电荷分布相似。当八个点电荷呈环状分布时,其圆环内可产生闭合的八边形及圆形等势线,其分布与图4中的环状分布相似。从图1(e)与1(f)可以看出,当点电荷分布较密时,其产生的等势线与线状电荷相似,当密度足够大时,即可产生与线状电荷相同的等势线。利用此方法来描绘线状电荷分布。
2 点-线与线-线电荷等势线分布
为了描绘线状电荷分布,我们将线电荷上的点离散为等距离的点电荷,再用格点法算出各格点的电势。表格1为直线形状分布的电荷离散为密度不同的点时,格点法算出的电荷周围各点的电势。
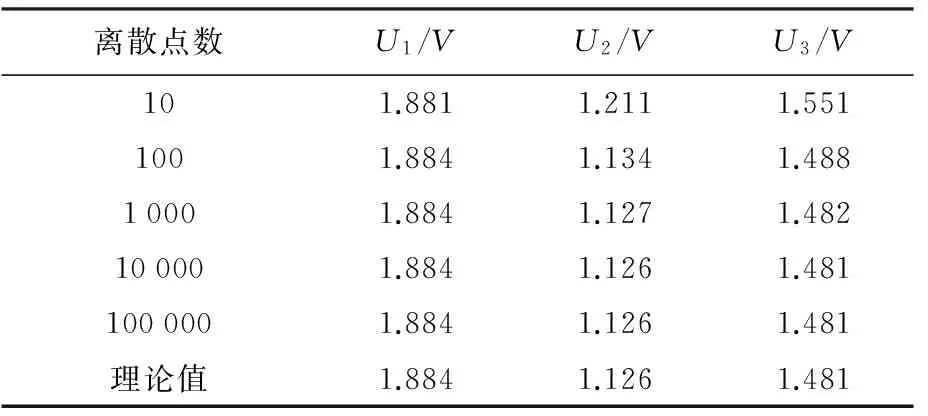
表1 直线形状电荷电势计算结果
表格1中,直线形状电荷长度为10米,其所带电量为10-9库仑。U1、U2与U3分别为距离直线中间与两端点4米处的电势值(如图2所示),计算中取无穷远为电势零点。此三点的理论公式为[5]。

(2)

(3)

(4)
从计算结果可以看出,当直线上的电荷离散的点数越多,其计算结果与理论值越接近。当散离点数为1万个点与10万个点时,计算结果完全相同,同时与理论结果也一致。从表格1可以看出,线状电荷电势随离散点数的增加,计算结果的准确度也增加。当离散的点数增加,而计算结果不变时,表明此离散点数的计算结果即为准确值。
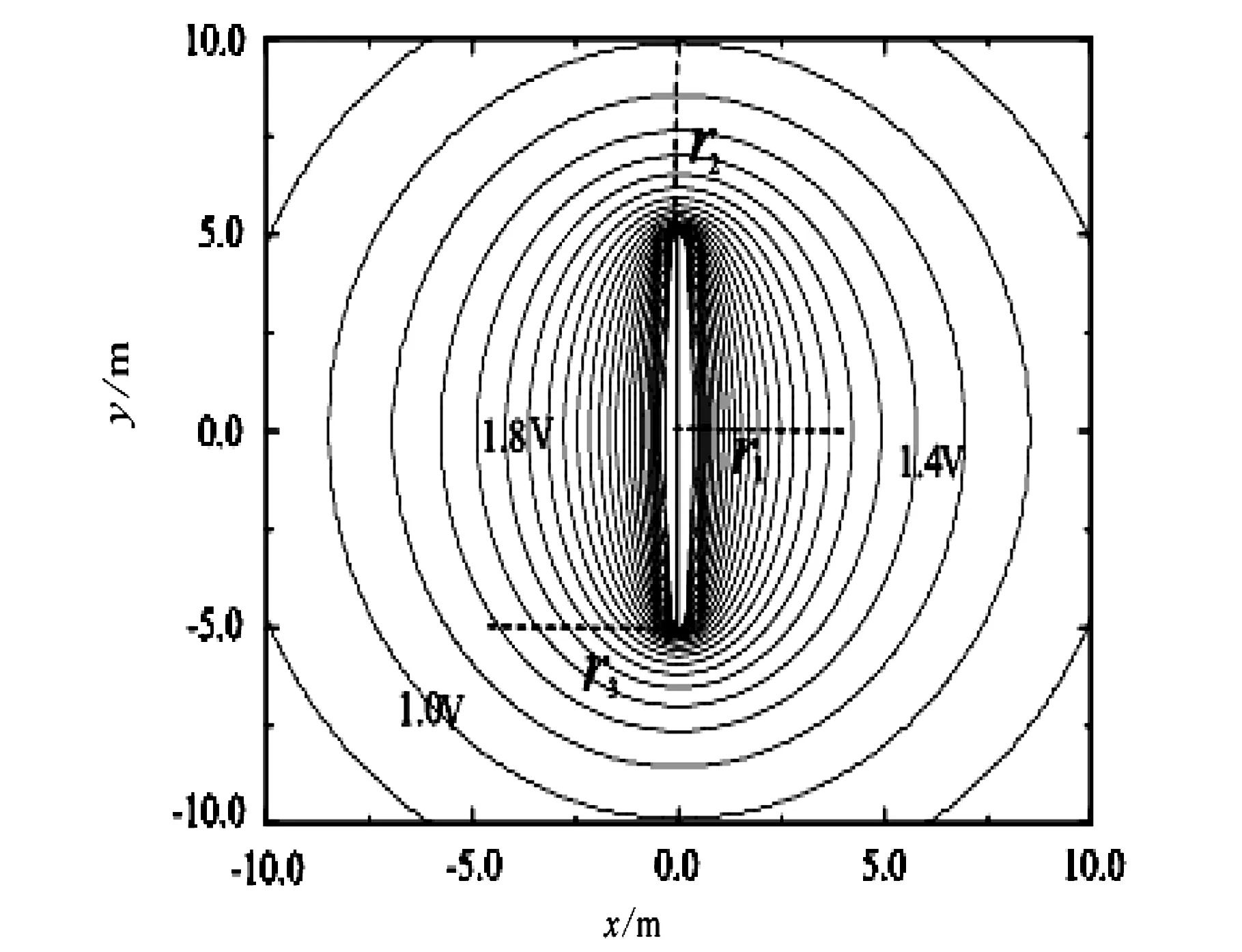
图2 直线形电荷等势线分布
图2中的等势线为线状电荷离散为1万个点时,格点法计算的结果。从图中可以看出,直线形电荷,在电荷附近处,直线两端处的等势线间距较小,分布较密,表明此处的场强较强。直线中间对应的等势线间距较大,分布较疏。离直线较远处,等势线趋于同心圆。
图3为利用格点法描绘的点-线与线-线电荷等势线分布情况图。其中,线电荷离散为1万个点电荷。图中的点与线所带电量相同。图3(a)中,受负点电荷影响,其对应的正直线形状电荷附近的等势线呈现中间细,两边粗的哑铃形状。图3(b)中,受正点电荷的影响,正直线形状电荷附近,
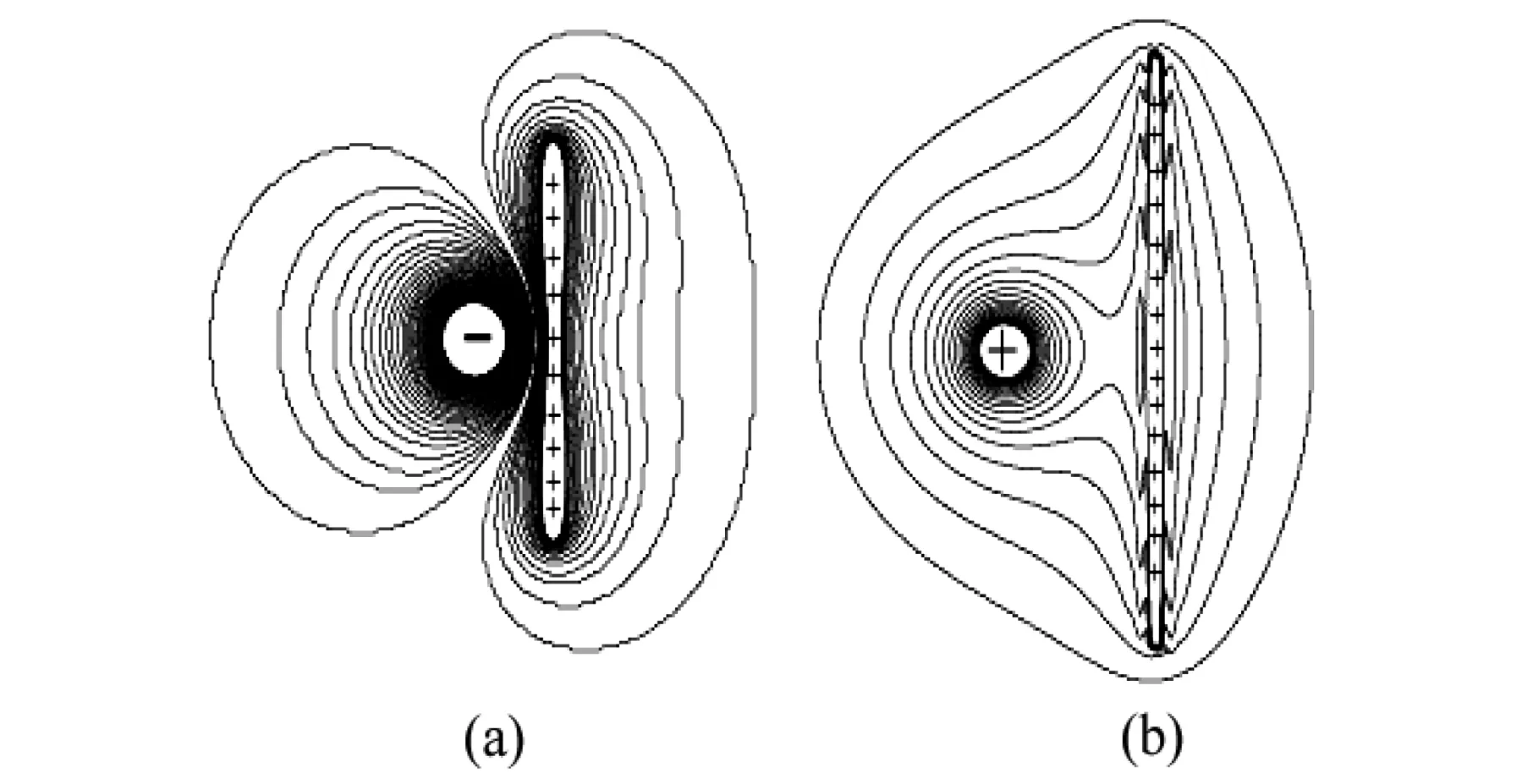
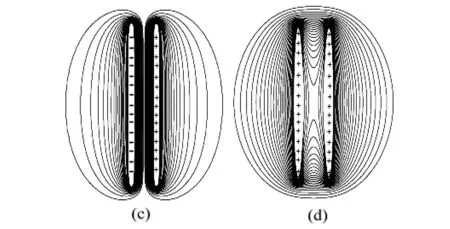
图3 点-线与线-线电荷等势分布
部分等势线出现小幅震荡。图3(c)与(d)的等势线分布情况与图1(a)与(b)中的点电荷等势线分布情况相似。
3 同心圆环形状电荷等势线分布
大学物理实验中,常用两同心圆环间的稳恒电流场来模拟同轴圆柱面间静电场电势分布,这容易使学生误以为模拟的是同心圆环间静电场电势分布。同心圆环与同轴圆柱面间的等势线分布是否相同呢?两个带等量异号同轴圆柱面间的等势线分布,其大小可由公式[6]。
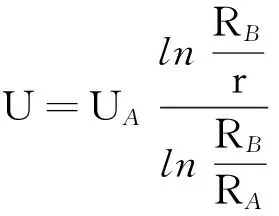
(5)
得到。上式中选取外圆柱面为电势零点,UA为两圆柱面间电势差,RA为内圆柱面半径,RB为外圆柱面半径,r为两圆柱面间任意一点到轴线距离。我们利用格点法模拟了两同心圆环间的等势线分布情况,并与同轴圆柱面间电势分布情况进行对比,其结果如图4所示。
图4(a)为同心圆环间的电势分布,图4(b)为同轴圆柱面间的电势分布。其中,内外圆柱面半径分别为1cm与5cm,两圆柱面间的电势差UA为10V,半径与电势差的取值与大学物理实验模拟静电场的仪器参数基本相同。理论计算可得同轴圆柱面间的电势差为
(6)
上式中Q为单位长度,内外圆柱面上分别所带的电量。当电势差UA为10V时,由公式(6)可得电量Q为3.455×10-10C。图4(a)中的内外圆环半径也分别为1cm与5cm,所带电量也为3.455×10-10库仑,圆环上电荷离散为1万个点,选取无穷远处为电势零点。
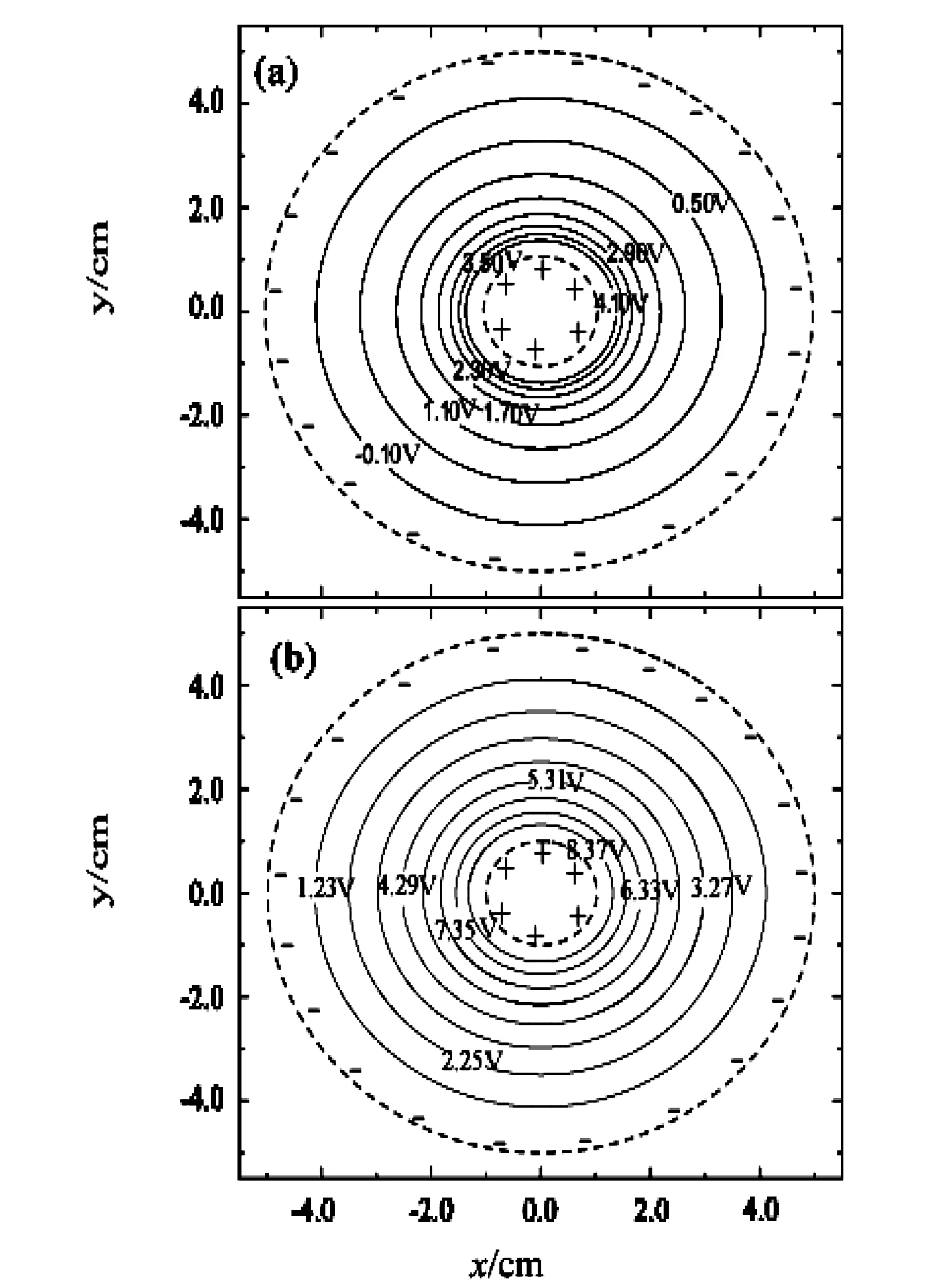
图4 同心圆环与同轴圆柱面等势线分布
图4(a)中每两条等势线间的电势差为0.60V,当距离圆心r为4.1cm处,其对应的电势为-0.10V,当距离圆心r为1.3cm处,其对应的电势为4.10V,两等势线间电势差为4.2V.图4(b)中,当距离圆心r为4.1cm处,其对应的电势为1.23V,当距离圆心r为1.3cm处,其对应的电势为8.37V,两等势线间电势差为7.14V。从图4(a)与图4(b)可以看出,同轴圆柱面与同心圆环产生的电势变化范围不同;两图中随半径r变小,等势线分布变密,其中同心圆环等势线变密速度更快。
4 结 论
利用格点法模拟了静电场等势线的分布,并利用离散的方法,模拟了直线形电荷及同心圆环形电荷的等势线。模拟结果表明,对于线状电荷,当离散的点数足够多时,即可得到准确的电势分布;同心圆环与同轴圆柱面间的等势线分布情况虽然相似,但并不完全相同。
从以上的计算结果可以看出,利用格点法描绘静电场电势,计算过程简单,计算结果准确,而且适用于描绘二维平面内,各种分布情况的点电荷与线状电荷的电势。希望利用该方法描绘的电势线能为学生更好的学习、理解静电场起到一定的帮助作用。
[1]毕升,叶红军.基于MATLAB的静电场模拟[J].大学物理实验,2013,26(4):89-91.
[2]陈伟,易志俊,丁益民.利用MATLAB模拟点电荷系的电场线和等势面[J].大学物理实验,2014,27(3):94-96.
[3]江俊勤.用格点法研究一个有趣的热传导问题[J].广东教育学院学报,2005,25(5):53-56.
[4]邹秀芬.对流扩散方程的格点模型[J].计算物理,1996,13(3):310-314.
[5]张孝林.大学物理(新版)学习指导[M].北京:科学出版社,2006:176.
[6]籍延坤,牛英煜.大学物理实验[M].北京:中国铁道出版社,2013:135.
Describing Electrostatic Field by Lattice Method
NIU Ying-yu,WANG Rong
(Dalian Jiaotong University,Liaoning Dalian 116028)
Theelectricpotentialofelectrostaticfieldisdescribedbylatticemethodintwodimensions.Thedistributionofequipotentiallinesinelectrostaticfieldforpoint-point,point-line,line-line,andconcentricringsaredescribed,andthecalculatedresultsarecomparedwiththeoreticalvalue.Thedifferentbetweenthetwoelectricpotentiallinesforconcentricringsandcentriccylindersisinvestigated.
latticemethod;electricpotential;pointcharge;linecharge
2016-04-13
辽宁省普通高等学校本科教育教学改革研究项目(UPRP20140719)
1007-2934(2016)04-0042-04
O4-33
ADOI:10.14139/j.cnki.cn22-1228.2016.004.014
——目镜套筒

