基于MGZZ准则的弹塑性模型隧道围岩参数敏感性分析★

李 秋 实

(1.同济大学岩土及地下工程教育部重点实验室，上海　200092；　2.同济大学土木工程学院，上海　200092)



·桥梁·隧道·

基于MGZZ准则的弹塑性模型隧道围岩参数敏感性分析★

李 秋 实1,2

(1.同济大学岩土及地下工程教育部重点实验室，上海200092；2.同济大学土木工程学院，上海200092)

广义三维非线性强度准则弹塑性模型中涉及的隧道围岩参数主要有弹性模量E、泊松比μ、地质强度指标GSI、岩石单轴抗压强度σci、岩石扰动系数D、完整岩石参数mi。通过有限元试验研究分析新奥法、新意法下各参数对拱顶沉降、周边收敛、掌子面挤出最终位移值的影响程度，以确定各参数对隧道围岩变形的敏感程度。结果表明：E，μ为极高敏感度参数，GSI为中敏感性参数；基于广义三维非线性强度准则的隧道围岩稳定性能研究与支护设计时应注重E，μ的赋值，并慎重调整。

MGZZ准则,新奥法,新意法,围岩参数,敏感性分析

0　引言

以新奥法为代表的隧道施工工法缺点有：1)无法彻底避免开挖面前方围岩体的塌方问题。2)难以解决初始衬砌和二次衬砌受力分担问题[1-6]。为克服上述缺陷，自20世纪70年代以来，意大利的Pietro Lunardi教授开始对数百座隧道进行理论和现场试验研究，并逐步创立了岩土控制变形分析法(ADECO-RS法)，该方法用中文解释为“新意法”。该法通过对开挖面前方超前核心土的超前约束和加固、控制隧道围岩的变形，实现全断面开挖[7]。

新意法的核心是精细分析开挖面前方的三维变形和稳定性，但有代表性的Mohr-Columb，Drucker-Prager强度准则因岩体的粘聚力和摩擦角工程现场难以准确确定，且依据室内试验结果取值粗糙，精细化分析程度低。本文采用一种三维非线性岩体强度准则(MGZZ)[8]，它是修正广义三维 Hoek-Brown强度准则[9](GZZ强度准则)中诸多参数的最佳拟合，其可完美解决屈服面不光滑的难题，且可方便、准确的应用到岩体隧道围岩三维变形分析。基于广义三维非线性强度准则的弹塑性模型参数有弹性模量E、泊松比μ、地质强度指标GSI、岩石单轴抗压强度σci、岩石扰动系数D、完整岩石参数mi。且文献[8]研究成果表明，上述参数对隧道围岩的稳定性能及支护设计均有一定的影响，但各参数的影响程度并未深入研究。然而，工程设计与施工中若全部考虑上述参数的影响，势必会造成工期和财力的极大浪费。为此，本文拟基于广义三维非线性强度准则，研究分析新奥法、新意法下上述参数对隧道围岩变形与稳定性的影响，以确定敏感程度较大的参量，为随后隧道工程的设计与施工提供理论指导和技术支持。

1　广义三维非线性强度准则与弹塑性模型

1.1广义三维非线性强度准则

Hoek-Brown 强度准则(即H-B强度准则)是1980年提出的一种针对节理岩体强度评估的方法，并于2002年引入岩体扰动因子D，该准则为二维的，没有考虑σ2的影响。此情况下H-B强度准则涉及4个敏感性分析参数，分别为地质强度指标GSI、岩石单轴抗压强度σci、岩石扰动系数D、完整岩石参数mi。岩石单轴抗压强度σci的计算公式如下：

(1)

其中，mb，s，a均为反映岩体特征的参数，mb为针对不同岩体的无量纲经验参数；s反映的是岩体的破碎程度，取值范围为0～1.0，完整岩体取值为1.0；a适用于质量较差的岩体。

然而，H-B强度准则未考虑中主应力σ2的影响，严格意义上无法进行隧道围岩的真三维变形分析。为此，Zhang和Zhu提出了一个真正意义上的三维Hoek-Brown强度准则[9]，Zhang将其广义扩展后可同时应用于岩石和岩体力学性能分析[10]，被国际同行命名为GZZ强度准则，其公式如下：

(2)

其中，σc为岩石的单轴抗压强度；τoct为八面体剪应力；σm,2为最大和最小主应力的平均值。

该准则已被诸多岩石力学研究者和工程技术人员广泛使用，但其屈服面不仅在三轴应力条件下且在三轴拉伸条件下呈凹形，导致某些应力路径时常出现问题，数值分析时很不方便。为解决这一难题，文献[8]提出采用三种光滑且满足全凸性的 Lode 势函数对GZZ强度准则进行修正，提出一个新的广义三维非线性强度准则，利用已有的岩石/岩体真三轴压缩试验数据进行屈服面光滑性、全凸性、强度预测精度的验证工作；并对广义三维非线性强度准则的参数进行最佳拟合，提出广义三维非线性强度准则(即MGZZ强度准则)参数的确定方法[11]。

根据笔者所在课题组历年试验获取的岩石真三轴实验数据[8]，采用最小二乘法(LS)对广义三维非线性强度准则的岩石参数mi进行最佳拟合，得出其mi比广义H-B强度准则的mi最佳拟合值大1，即广义三维非线性强度准则的mi应增加1。基于地质强度指标GSI，MGZZ强度准则的岩体参数mb，s，a的取值方法如下：

(3)

(4)

(5)

其中，GSI，mi分别由文献[11][12]得到；D为岩体参数，反映爆破影响和应力释放引起扰动的程度，取值范围为0～1.0，现场无扰动岩体为0，非常扰动岩体为1.0。

1.2基于非线性强度准则的弹塑性本构模型

朱合华等(2016)提出基于三维非线性强度准则的弹塑性本构模型，采用分段隐式修正的塑性流动法则，很好地反映了岩石在不同的围压条件下应力—应变规律[13]。该塑性流动法则的主要特点是以两个插值系数来描述围压对于塑性变形的影响，直接对关联流动形式的流动矢量进行修正，避免构造形式复杂的塑性势函数显式表达式。在无侧限条件、高围压条件和三轴拉伸条件下，岩石材料塑性流动可分别近似退化为关联流动、常体积流动和最大拉应力流动，同时将一般状态下的塑性流动定义为这三种情况之间的插值来进行处理。该三维弹塑性本构模型的优点在于不仅考虑了不同围压条件下的岩石塑性变形规律，而且保证了塑性势函数在整个主应力空间中的连续性，同时没有引入更多附加参数。

综上，广义三维非线性强度准则主要涉及弹性模量E、泊松比μ，地质强度指标GSI，岩石单轴抗压强度σci，岩石扰动系数D，完整岩石参数mi，岩体参数mb,s,a等9个参数，其中岩石单轴抗压强度σci可由参数mb，s，a通过式(1)得到。下文将通过数值试验对广义三维非线性强度准则中E，μ，σci，GSI，mi，D等参数进行敏感性分析研究，获取高敏感度参数，以指导隧道工程的设计与施工。

2　参数敏感性分析方法与设置

2.1数值模型建立

数值模型试验采用同济曙光三维有限元分析软件(2.0版)进行[14]，采用基于广义三维非线性岩体强度准则的弹塑性模型分析。

隧道断面尺寸设置为宽×高=15 m×10 m，由4种不同半径的7个圆弧组成。设定隧道外围为3 m厚锚杆加固区，喷射180 mm厚C20混凝土作为初期支护，350 mm钢筋混凝土作为二衬，同时新意法的掌子面加固采用超前砂浆锚杆实现。新奥法采用6步台阶法，新意法为全断面开挖。新奥法、新意法数值模型见图1，图2。

图1　新奥法隧道数值模型　　　　　图2　新意法隧道数值模型

如图1，图2所示，新奥法与新意法数值计算模型尺寸一致，但隧道开挖部分划分的块体数量存在差异，对应的初衬、二衬及锚杆作用区块体大小并不相同，新奥法及新意法计算模型的块体数量分别为21和6。为减小边界效应的影响，左右边界尺寸取4倍于隧道直径，上下边界尺寸取5倍于隧道直径。模型整体尺寸为60 m×50 m×30 m，隧道上覆岩层分别为25 m，55 m和85 m，围岩级别分别选用Ⅳ，Ⅴ，Ⅵ级三种。受篇幅所限，在此仅对上覆岩层25 m，围岩级别为Ⅴ级的工况分析说明。

2.2围岩参数敏感性研究方法与参数设置

采用上述模型，开挖步距1 m，支护方式为初衬+二衬+锚杆作用区，新意法添加核心锚。原岩作为基准参数值，密度不变；改变其他6种参数，实行1种参数改变，另5种参数不变，改变幅度分别为±30%的方式，形成6种工况，12种计算模型，提取计算过程中拱顶下沉、周边收敛、掌子面挤出的最终位移量数据，并与基准参数值下的计算数据对比分析，以研究确定上述6种围岩参数的敏感性。参数的敏感性判定见表1。

模型试验采用的围岩参数见表2，表中抗压强度参数改变方式为调整荷载大小，即摒弃自重加载，施加相应荷载实现抗压强度的调整；结合文献[8]设置各围岩敏感性参数见表2。由式(3)～式(5)获取mb,s,a，进而选定模型本构关系，从而得到最大主应力σ1、中主应力σ2、最小主应力σ3，最后进行参数敏感性的数值分析研究。

表1　参数敏感度判定表

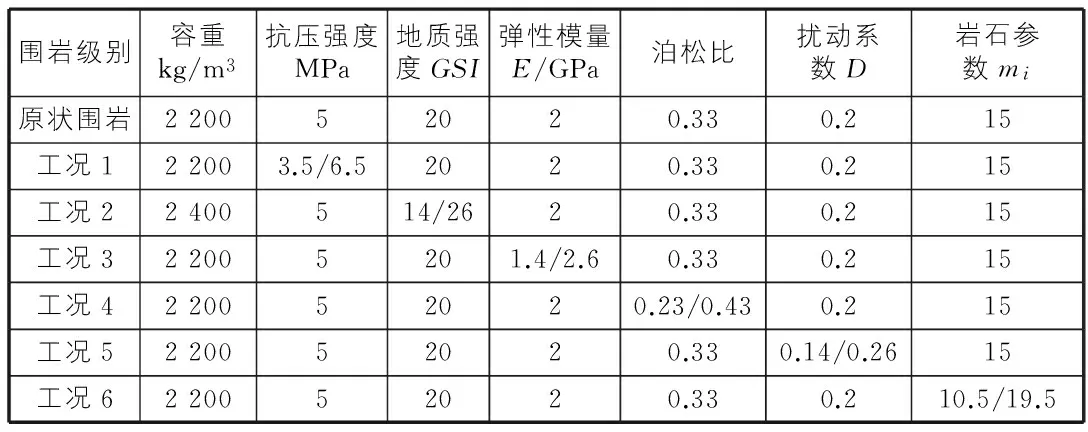
表2　围岩敏感性分析参数设置

3　数值分析结果

3.1基于新奥法的参数敏感性分析

针对12个参数变化模型、1个基准值模型进行分析数据的提取，提取断面距洞口1 m，获取隧道开挖结束后拱顶沉降、边墙收敛、掌子面挤出的最终位移量。将参数变化模型的围岩变形与基准值模型的围岩变形对比，计算得到较基准值模型变形的百分比，形成图3～图5。

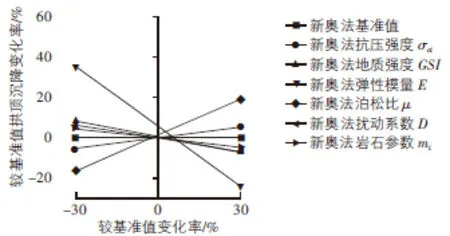
图3　新奥法隧道拱顶下沉偏离基准值

图4　新奥法隧道边墙收敛偏离基准值

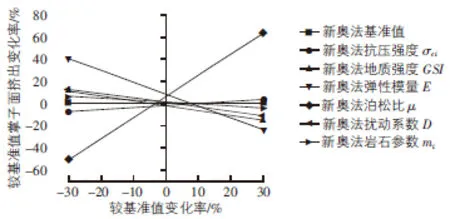
图5　新奥法隧道掌子面挤出偏离基准值

分析图3～图5可知，各参数的敏感性排序如下：E>μ>GSI>D>σci>mi，弹性模量E、泊松比μ均为极高的敏感度参数。E由-30%变化至30%时，隧道的拱顶沉降、周边收敛及掌子面挤出较基准值变化幅度均超过30%，拱顶沉降、边墙收敛、掌子面挤出的变形量占比分别为35%,45%和40%。μ由-30%变化到30%时，隧道边墙收敛变化范围达到83%；对隧道边墙收敛的影响远大于对拱顶沉降的影响；掌子面挤出次之，达63%。地质强度指标GSI对拱顶沉降为低敏感度参数；对边墙收敛和掌子面挤出为中敏感度参数，分别达到16%和15%。开挖扰动系数D对周边收敛为中敏感度参数，达到14%，对拱顶沉降和掌子面挤出位移量的影响则为低敏感度参数。岩石单轴抗压强度σci、材料参数mi则为低敏感度参数。

3.2基于新意法的参数敏感性分析

与新奥法相同，新意法的参数敏感性分析同样是针对12个参数变化模型、1个基准值模型进行数据提取，提取断面距洞口1 m，获取隧道开挖结束后拱顶沉降、边墙收敛、掌子面挤出的最终位移量；并将参数变化模型的围岩变形与基准值模型对比分析，计算得到较基准值模型变形的百分比，形成图6～图8。

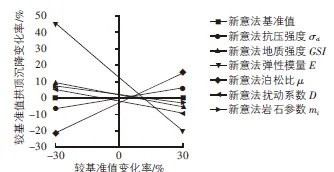
图6　隧道拱顶下沉偏离的基准值

图7　隧道边墙收敛偏离的基准值

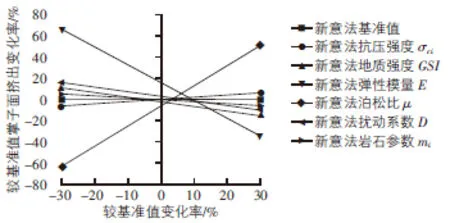
图8　隧道掌子面挤出偏离的基准值

分析图6～图8可知，新意法中各参数的敏感性排序同样如下：E>μ>GSI>D>σci>mi，弹性模量E、泊松比μ同样均为极高敏感度参数。E由-30%变化至30%时，隧道的拱顶沉降、周边收敛及掌子面的挤出位移量较基准值的变化范围分别为45%，55%，65%。μ由-30%变化到30%时，隧道边墙收敛变化范围达到84%，泊松比对隧道边墙收敛和掌子面挤出的影响同样远大于对拱顶沉降的影响。地质强度指标GSI对拱顶沉降为低敏感度参数；对边墙收敛和掌子面挤出为中敏感度参数，分别达到16%和15%。开挖扰动系数D对周边收敛的影响为中敏感度参数，为14%，对拱顶沉降和掌子面挤出的最终位移量为低敏感度参数。与新奥法相同，岩石单轴抗压强度σci、材料参数mi同样均为低敏感度参数。

3.3参数敏感性分析结果

通过上述分析结果可知，新奥法与新意法中各参数敏感性的表现基本一致，即E>μ>GSI>D>σci>mi。部分参数状况下新意法开挖时拱顶下沉、边墙收敛、掌子面挤出变化率幅度均比新奥法大，原因在于开挖方法的差异。两种工法下弹性模量E、泊松比μ均为极高敏感度参数，弹性模量E由-30%变化至30%时，隧道拱顶沉降、周边收敛、掌子面挤出位移的最终值较基准值变化范围均超过30%；μ变化相同幅度时隧道周边收敛的变化范围达到80%，对隧道边墙水平位移的影响远超过拱顶沉降，处于中间位置的为掌子面挤出位移。地质强度指标GSI对拱顶沉降为低敏感度参数，对掌子面挤出为中敏感度参数；对边墙收敛新奥法下为中敏感度参数，新意法下为高敏感度参数，达到20%。扰动系数D对周边收敛的影响程度为中敏感度参数，对拱顶沉降的影响为低敏感度参数，对掌子面挤出位移的最终量，新奥法下为低敏感度，新意法下为中敏感度。两种工法下岩石单轴抗压强度σci、材料参数mi同样均为低敏感度参数。

4　结语

基于本课题组已有的研究成果，通过有限元数值分析研究了新意法、新奥法下广义三维非线性强度准则中各参量对隧道围岩变形的敏感性。主要结论如下：1)广义三维非线性强度准则主要需要辨识的参数有弹性模量E、泊松比μ、地质强度指标GSI、岩石单轴抗压强度σci、岩石扰动系数D、完整岩石参数mi。2)两种工法下广义三维非线性强度准则中弹性模量E、泊松比μ为极高敏感度参数，GSI为中敏感性参数，岩石单轴抗压强度σci、材料参数mi同样均为低敏感度参数。

下一步基于广义三维非线性强度准则的隧道围岩三维稳定性与支护设计研究中应注重E，μ的赋值，且计算参数调整时需慎重，使得研究成果尽量贴近实际工况，以指导隧道工程的设计与施工。

[1]张新亮.大断面隧道CD法施工围岩应力行为研究[D].成都：西南交通大学硕士学位论文，2008.

[2]丁伯阳，王军杰.偏压隧道CD法导坑开挖顺序数值分析[J].浙江工业大学学报(自然科学版)，2010，38(6)：633-637.

[3]Eberhard F.The Mount Baker tunnel/USA(Exemplary for drivage of major cross sections in soft soil)[J].Tunnel,1990(4)：205-220.

[4]黄明琦，付贤伦，李云超.大断面海底隧道软弱地层CRD法施工稳定性控制研究[J].岩石力学与工程学报，2007，26(S2)：3084-3089.

[5]郝小苏，金露，何远康.双向八车道公路隧道双侧壁导坑法施工优化[J].现代交通技术，2008，5(1)：61-64.

[6]李慎文.双侧壁导洞法通过断层破碎带[J].石家庄铁道学院学报，1999，12(S1)：24-26.

[7]Pietro L.The design and construction of tunnels using the app roach based on the analysis of controlled deformation in rocks and soils[J].Tunnels & Tunneling International ADECO-RS Approach,2000(5):3-30.

[8]张琦.广义三维Hoek-Brown岩体强度准则的修正及其参数多尺度研究[D].上海：同济大学博士学位论文，2013.

[9]Zhang L.Y,Zhu H.H.Three-dimensional Hoek-Brown strength criterion for rocks[J].Journal of Geotechnical and Geoenvironmental Engineering,2007,133(9):1128-1135.

[10]Zhang L.Y.A generalized three-dimensional Hoek-Brown strength criterion[J].Rock Mech-anics and Rock Engineering,2008,41(6):893-915.

[11]Zhang Q,Zhu HH,Zhang LY. Modification of a generalized three-dimensional Hoek-Brown strength criterion[J].International Journal of Rock Mechanics and Mining Science,2013(59):80-96.

[12]Hoek E.实用岩石工程技术[M].郑州：黄河水利出版社，2002.

[13]朱合华，黄伯麒，张琦，等.基于广义Hoek-Brown准则的弹塑性本构模型及数值实现[J].工程力学，2016,33(2):41-49.

[14]同济大学.同济曙光GeoFBA2D公路隧道设计模块用户手册[Z].2003.

Sensitivity analysis of surrounding rock parameters based on elasto-plastic model with MGZZ strength criterion★

Li Qiushi1,2

(1.TongjiUniversity,ResearchCenteronGeotechnicalandUndergroundEngineeringofChineseEducationMinistry,Shanghai200092,China;2.CollegeofCivilEngineering,TongjiUniversity,Shanghai200092,China)

In the elasto-plastic model with Modified Generalized Zhang-Zhu(MGZZ) strength criterion, elastic modulusE, Poisson’s ratioμ, uniaxial compressive strengthσci, geological strength indexGSI, intact rock parametermi, disturbance factorDare main parameters of surrounding rock. The sensitivity of these parameters has been analyzed by FEM in view of New Austrian Tunneling Method and ADECO-RS Method. The results show that the elastic modulusEand Poisson’s ratioμare extremely high sensitivity parameters, geological strength indexGSIis the medium sensitivity parameters. ParametersEandμshould be specially emphasized and carefully adjusted in the tunnel support design.

MGZZ criterion, New Austrian Tunneling Method, ADECO-RS Method, parameters of surrounding rock, sensitivity analysis

1009-6825(2016)21-0155-04

2016-05-19★:国家自然科学重点基金项目“隧道围岩稳定性三维精细化模拟方法与应用”(项目编号：411330751)

李秋实(1985- )，男，在读硕士

U451.2

A