遗传算法在矮塔斜拉桥索力优化中的应用★

罗　敏　胡世翔

(1.南京航空航天大学金城学院，江苏 南京　211156；　2.东南大学交通学院，江苏 南京　210096)



遗传算法在矮塔斜拉桥索力优化中的应用★

罗敏1胡世翔2

(1.南京航空航天大学金城学院，江苏 南京211156；2.东南大学交通学院，江苏 南京210096)

结合ANSYS参数化编程，基于MATLAB软件编制相应的优化程序，以一座多跨矮塔斜拉桥为例，选择主梁弯曲应变能最小为优化目标，将遗传算法的基本原理应用于桥梁结构的索力优化计算中，优化结果表明结构受力得到了有效改善。

矮塔斜拉桥，遗传算法，索力，结构优化

1　概述

矮塔斜拉桥是由主梁、索塔和拉索三部分构成的组合结构体系，是一种介于连续梁桥和斜拉桥之间的桥型，近十几年来在我国得到广泛应用。2000年建成的主跨312 m的芜湖长江大桥是我国首座矮塔斜拉桥，它采用钢桁主梁，是公铁两用桥。2001年建成的主跨132 m的漳州战备桥是我国首座预应力混凝土矮塔斜拉桥，随后又建成了兰州小西湖黄河大桥(主跨136 m，桥长300 m)、广州番禺沙湾特大桥(主跨248 m，桥长523 m)、宁江松花江特大桥(主跨150 m，桥长640 m)、长海县长山大桥(主跨260 m，桥长540 m)等一系列矮塔斜拉桥[1]。

矮塔斜拉桥是由梁、塔、索为主要构件的高次超静定结构，其索力大小对结构内力和变形有重大影响，而该桥型一般进行多跨布置，其索力优化存在自变量多、结构计算复杂、结构存在非线性等难点。本文结合ANSYS参数化编程，将遗传算法应用于桥梁结构的索力优化中，适用于自变量较多的多跨结构，在ANSYS模型中可以方便的考虑非线性问题，通过改变模型中的输出结果，可以方便地选择内力、变形或者应力为优化目标。

2　索力优化相关理论

确定索力是斜拉桥设计中关键的技术问题。斜拉索的张拉对斜拉桥的施工、成桥、运营直至破坏整个过程的受力都有很大的影响。因此需要合理地确定拉索索力，使得斜拉桥受力的全过程均处于合理状态。

国内外对斜拉桥的索力优化方法开展了多年的研究，国内外学者做了很多的研究工作并提出了合理实用的优化计算方法。常用的索力优化方法均以成桥恒载受力状态作为目标，采用目标函数和约束条件进行优化，以保证斜拉桥在成桥恒载作用下内力最优。其中比较有代表性的方法有影响矩阵法、应力平衡法、弯矩可行域法等[2-4]。一般情况下，根据这些方法建立的索力优化数学模型可归结为线性最小二乘优化问题，可采用相应的迭代算法进行求解。

以常用的影响矩阵法为例，斜拉索索力作为施调向量{T}，通过影响矩阵{C}，建立受调向量与施调向量之间的关系，即{D} ={C}{T}。若以弯曲应变能为目标函数，受调向量应为主梁的弯矩{M}，则有：

{M}={M0}+{C}+{T}

(1)

其中，{M0}为受调弯矩的初值。结构的应变能U可写为：

(2)

其中，li，Ei，Ii，Mi分别为结构单元的长度、弹性模量、惯性矩和弯矩。式(2)可以改写为：

U={M}T{B}{M}

(3)

其中，{B}=diag(b1,b2,…,bi)，bi=li/2EiIi。

将式(1)代入式(3)中，可得：

U={T}T{C}T{B}{C}{T}+

{T}T{C}T({B}T+{B}){M0}+c0

(4)

其中，c0为与{T}无关的常数。式(4)即为根据弯曲能量建立目标函数，属于数学上的线性最小二乘优化问题。

3　遗传算法基本原理

3.1遗传算法计算步骤

遗传算法是一种基于自然进化规则的随机搜索算法，与传统优化方法相比，具有全局优化、群体搜索、鲁棒性强、易于并行化等优点。其计算的基本步骤如图1所示。

3.2遗传算法优化方法在桥梁结构中的实现

将遗传算法应用于桥梁结构索力优化中，得到与自变量(一般为索力)对应的优化目标值(一般为弯曲能量、弯矩值等) 是一个难点，对于简单结构可以建立两者之间的函数关系或者采用影响矩阵法。本文基于MATLAB软件编制相应的遗传算法程序，结合ANSYS参数化编程的方法，在优化中调用ANSYS软件计算和自变量对应的结构内力状态，可以适用于多跨复杂结构，具体计算原理为：1)MATLAB软件中生成自变量的初始种群，并将自变量量结果写入文件中；2)ANSYS APDL文件中读入自变量数值；3)ANSYS中进行结构计算，并输出结果(弯曲能量等目标函数结果)到文件中；4)MATLAB中读取ANSYS输出结果并计算种群的适应度；5)MATLAB中根据适应度进行种群的选择及交叉、变异；6)生成新的种群，并将结果写入文件中；7)重复2)～6)直到满足要求。

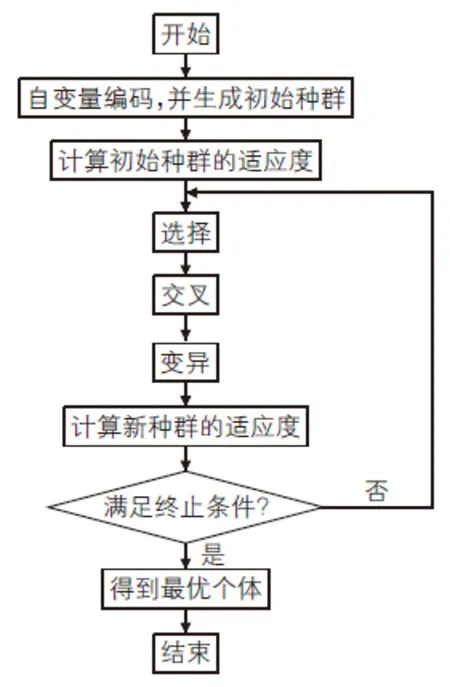
图1　遗传算法计算流程图

4　实例分析

4.1实例介绍及建模方法

以某4塔5跨矮塔斜拉桥为例，跨径布置为95 m+3×150 m+95 m，边跨与主跨跨径比为0.633，预应力混凝土主梁采用变截面，梁高3.0 m～5.5 m，塔高23.5 m。采用单索面—双排索的拉索布置形式，单根拉索由40根15.24 mm的钢绞线构成，桥型布置见图2。

图2　加载工况示意图(单位：m)

有限元模型见图3，主梁、桥墩、塔采用Beam44梁单元，斜拉索采用Link8杆单元，降温法实现索力施加。边界条件为：2号桥墩、塔和主梁固结，墩的底面为固结约束，其他3个桥墩与主梁分离，主梁作用于支座上，建模时不需建立桥墩，对支座处主梁底面施加约束。按照设计要求，支座起竖向支撑的作用，释放纵桥向的水平约束和绕横桥向的转动约束。

图3　有限元模型

4.2结构优化结果

以主梁弯曲应变能最小为优化目标，以主梁上下缘应力为约束条件，采用文中的遗传算法优化后结果见图4～图7。

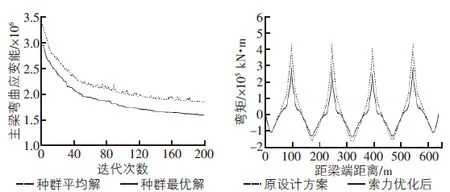
图4　遗传算法优化迭代过程　　　图5　结构恒载内力

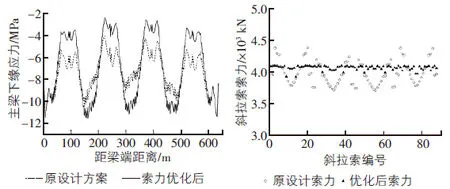
图6　结构恒载应力　　　　　图7　结构索力

由图4可知，随着迭代计算，结构弯曲应变能迅速减小，迭代次数超过100代后，接近最优解。由图5，图6可知，优化后主梁恒载弯矩得到改善，跨中最大正弯矩和墩顶负弯矩均大幅减小，同时跨中附近梁段的压应力储备得到提高。由图7可知，基于最大索力不变的情况下，结构中索力分布更为均匀。

5　结语

结合ANSYS参数化建模，将遗传算法应用于多跨矮塔斜拉桥的索力优化，通过分析优化前后结构的受力状态，可以得到如下结论：

1)结合ANSYS软件，遗传算法可以方便地应用于大型复杂结构的索力优化分析，尤其是多自变量的优化分析。

2)在优化后总索力接近原设计总索力的前提下，通过调整索力分布，优化后结构的内力得到改善，跨中最大正弯曲和墩顶最大负弯矩明显减小。

[1]陈从春.矮塔斜拉桥设计理论核心问题研究[D].上海:同济大学博士学位论文,2006.

[2]徐金勇.ANSYS优化设计在确定斜拉桥恒载索力中的应用[J].山西建筑,2012,38(17):218-220.

[3]郑一峰.混凝土部分斜拉桥设计理论研究[D].哈尔滨:哈尔滨工业大学博士学位论文,2005.

[4]HASSAN M M.Optimization of stay cables in cable-stayed bridges using finite element,genetic algorithm,and B-spline combined technique[J].Engineering Structures,2013(49):643-654.

Determination of cable forces for extradosed bridges with genetic algorithm★

Luo Min1Hu Shixiang2

(1.JinchengCollege,NanjingUniversityofAeronauticsandAstronautics,Nanjing211156,China;2.SchoolofTransportation,SoutheastUniversity,Nanjing210096,China)

A program is developed based on MATLAB software and ANSYS software. A multi-span extradosed bridge is cited as an example and was analyzed. With objective function the minimum strain energy of main beam, the genetic algorithm is applied to the optimization of cable forces of bridges, optimized structure has improved mechanical condition.

extradosed bridge, genetic algorithm, cable forces, structure optimize

1009-6825(2016)21-0160-02

2016-05-15★:江苏省高校自然科学基金项目(项目编号：15KJD580001)

罗敏(1986- )，女，讲师；胡世翔(1986- )，男，在读博士

U448.27

A