全站仪三角高程测量在软基监测工程中的应用

杨帅东　覃在诚　黄志怀

(1.珠江水利委员会珠江水利科学研究院，广东 广州　510611；　2.广东华南水电高新技术开发有限公司，广东 广州　510611)



·测量·

全站仪三角高程测量在软基监测工程中的应用

杨帅东1覃在诚2黄志怀1

(1.珠江水利委员会珠江水利科学研究院，广东 广州510611；2.广东华南水电高新技术开发有限公司，广东 广州510611)

介绍了全站仪三角高程测量的原理，分析了影响其精度的主要误差来源，并结合实例，阐述了全站仪三角高程测量法在软基监测工程中的运用，并对其观测精度进行了估算，指出全站仪三角高程测量法具有不受地形影响、施测速度快、作业灵活等优点。

三角高程测量，高差中误差，球气差，软基监测

0　引言

垂直位移观测是常规的测量技术之一，它主要有水准测量、电磁波测距三角高程测量、GPS拟合高程测量三种，测定地面点高程的传统方法主要采用几何水准法，它是利用水准仪提供的水平视线，测定两点间的高差，从而推算出地面点的高程，测量精度虽高，但其劳动量大，容易受地形的限制。随着现代测量技术的发展、工程的实际需要和仪器精度技术的跨越性突破，高精度的全站仪在变形监测中逐渐得到普及，应用领域也越来越广泛，例如：建筑物的变形监测、隧道施工、精密小型三角网、桥梁施工、坝体监测、地形测量等等。

随着人们对全站仪更深入的了解和对全站仪三角高程测量的大量研究分析，发现全站仪三角高程测量法能够代替水准法在高差起伏大的地形作业[2]。三角高程测量和传统的水准测量相比，它具有不易受高差起伏大的地形影响，且施测速度快，作业灵活等优点，因此，在软基监测工程中，如能使用全站仪三角高程测量法，将会极大地减少工作强度。

1　工程概况

广州市南沙区某软基工程，场区位于珠江河口地区，区内河网密布，软土深厚，土质多为软塑～流塑状态的细粒土，如淤泥、高压缩性饱和粘性土、粉土，其天然含水量高、容重小、渗透系数小、抗剪强度低，在荷载作用下，容易产生较大的沉降变形或失稳，属于软弱地基。采用堆载预压法处理软弱地基，在堆载过程中对其进行监测，本工程对软基的监测内容有：地表沉降观测、孔隙水压力观测、分层沉降观测、水平位移观测、深层水平位移观测。其中，地表沉降观测用于控制土方填筑速率，防止因填筑过快而导致软土地基发生深层剪切破坏。设计沉降观测采用埋设沉降板的方法，因工程场地处于南方河网地区，地形条件差，现场干扰多，监测频率高，常规水准测量方法难以实施，在实际监测过程中，根据项目特点，采用全站仪三角高程法进行四等水准沉降观测。

2　三角高程测量的基本原理

如图1所示，假设A和B分别为地面上的两个点，S为AB两点间的斜距，i为仪器高，v为目标高，角α为从A观hAB测B的垂直角，A点的高程已知，为HA，B点高程未知，欲求HB的高程，计算式为：

HB=HA+hAB

(1)

hAB=Ssinα+i-v

(2)

计算时通过三角函数关系算出望远镜和棱镜之间的高差，然后用其高差加上仪器高i减去棱镜高v得出AB两点间的高差。

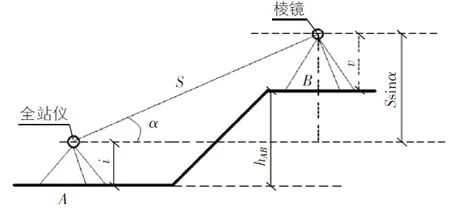
图1　三角高程测量原理图

上述公式在AB两点间的距离较近时适用，当距离间隔远时，需加入球气差的改正[1]，计算式变为：

(3)

3　全站仪三角高程测量在软基地表沉降监测中的运用

在实际的测量工作中，测量人员在稳固牢靠、视线良好的地方贴上反射片作为测量基点，然后通过场区外的控制点引测出其高程，并定期复核，同时也在沉降观测标的顶部贴上反射片，作为监测点，施测时，不必量取仪器高和反射片所贴的高度，也无需输入测站点的高程，全站仪任意安置在一个距离合适的地方，后视基点反射片A的中心点，读取斜距和竖直角，仪器测量界面里显示的高差即为望远镜与反射片A之间的高差h1，同理可得到前视反射片B与仪器的高差h2，两者相减即可得出反射片A与反射片B之间的高差hAB，具体如下。

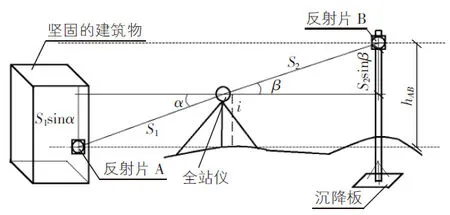
图2　全站仪沉降观测图

如图2所示，假设反射片A贴在坚固的建筑物上，其高程为HA，S1为后视时的斜距，α为其竖直角，根据三角函数关系式得：

h1=S1sinα

(4)

同理可得：

h2=S2sinβ

(5)

其中，h1，h2分别为后视与前视的高差。式(5)减式(4)得两点间的高差hAB，则反射片B的高程HB为:

HB=HA+hAB=HA+(h2-h1)

(6)

记第一次测量反射片B的高程为HB1，第二次为HB2，则两次高程之差即为本次观测的沉降量。用这种三角高程测量的方法能快速测出高差起伏大的沉降监测点高程，无需人工读数，与传统的水准测量相比，效率更高。

4　精度估算

1)由于此方法不必输入仪器高和目标高，因此不存在量取的误差，在以下的高差计算公式中，仪器高和目标高不再参与计算。

2)球气差对高差会产生一定的影响，计算式为[6]:

(7)

以图2为例，那么加上球气差改正式的一测站前后视的高差分别为：

h1=S1sinα+f1

(8)

h2=S2sinβ+f2

(9)

其中,f1，f2分别为后视与前视的球气差改正式。则反射片A与反射片B之间的高差为：

hAB=h2-h1=S2sinβ-S1sinα+f2-f1

(10)

理论上，当大气折光系数K和地球曲率半径R的值一定，前后视距D相等时，结合式(10)，f2=f1，相减为0，因此，球气差对高差的影响基本抵消。在实际测量过程中，把仪器架设在两断面的中间位置，使测量前后视距相等，那么球气差对高差的影响就能够得到很大程度上的消减。

在不同的环境条件下，全站仪测量反射片的最远视线长度会有所不同，且全站仪望远镜的放大倍数有限，反射片的规格大小为4 cm×4 cm，视线过远会影响其成像质量，因此，为了保证测量精度，全站仪的视线最远长度按照四等水准测量所规定的100 m进行测量。

假设测量前后视的K值在短时间内是相等的，水网地区K值的取值范围为0.15～0.16[3]，在这里取0.16，当前后视距不相等时，球气差对一测站高差的影响如表1所示。

从表1中可以看出，球气差对高差的影响随视距的减小而减小，随前后视距差的增大而增大。视距差越小，球气差的影响就越小，当视距差为0时，球气差的影响理论上也为0。因此，根据实际的工程需要，出于现场干扰多，监测频率高，要保证前后视距相等较为困难的原因，在测量时，缩短视线长度同时使前后视距尽量相等以减弱球气差的影响，在高差计算时，不进行球气差改正。

3)不考虑球气差的影响，根据误差传播定律得，计算一测站高差中误差为[6]：

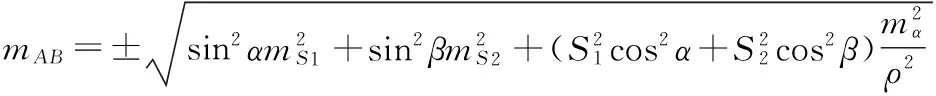
其中，mS和mα分别为测距中误差和测角中误差；mα/ρ化成弧度，ρ=206 265″[4]。

当测量最远的视线长度前后视距各为100 m时，设前后视观测的垂直角相等，4 cm×4 cm的反射片在标准测量模式下的测距精度为2+2 ppm，全站仪的测角精度分别为1″和2″，计算用不同测角精度的仪器观测不同垂直角时一测站高差中误差(如表2，表3所示)。

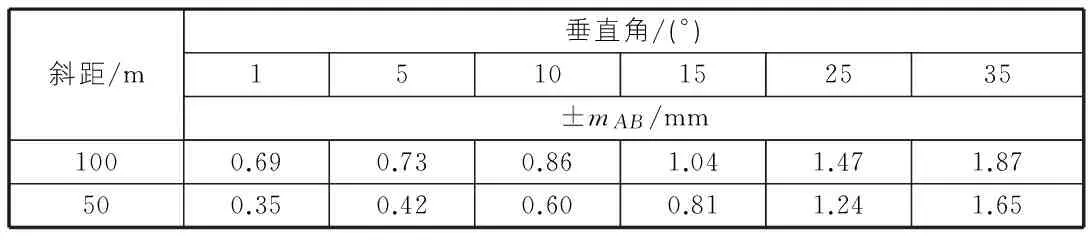
表2　全站仪(1″，2+2 ppm)一测站高差中误差

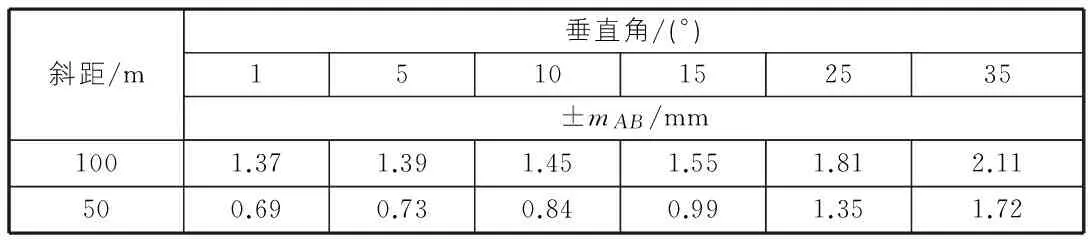
表3　全站仪(2″，2+2 ppm)一测站高差中误差

从表2，表3中可以看出，仪器的测角精度和观测垂直角的大小、测距的长远，是影响一测站高差测量精度的重要因素。

4)单向观测时每千米高差中误差计算式为[7]：

(11)

其中，mAB为高差中误差；L为前后视距之和。以表3的数据为例，计算每千米的高差中误差，并取2倍的中误差作为容许误差[4]，计算结果见表4。

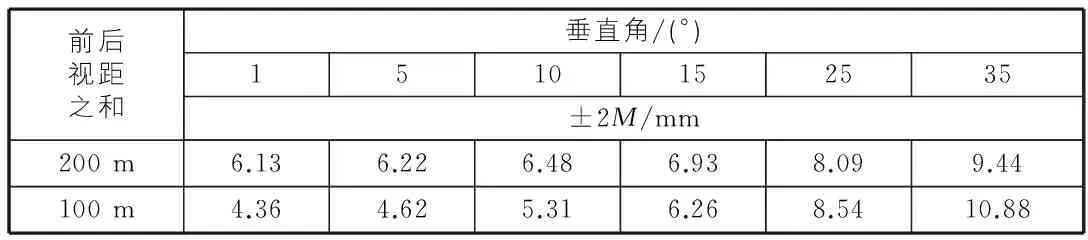
表4　全站仪(2″,2′+2 ppm)的容许误差

5　结语

1)这种全站仪三角高程测量的方法测量速度快，受地形的限制较小，架设全站仪的位置较为灵活方便。

2)无需量取仪高和目标高，减少三角高程测量的误差来源，使用反射片贴在监测点上进行测量，降低了劳动强度。

3)虽然不考虑球气差的影响，但是在测量时也应使前后视距尽量相等，以减弱大气折光的影响。

4)该方法的测量精度会随着观测垂直角的增大而降低，使用反射片测量也使得观测的视线长度有限，因此不适宜进行长距离和较大的垂直角观测，同时，对所选仪器的测量精度有一定的要求。

[1]张前勇,常胜.全站仪水准法三角高程测量的探讨[J].湖北民族学院学报,2007,25(1):42-45.

[2]张智韬,黄兆铭.全站仪三角高程测量方法及精度分析[J].西北农林科技大学学报,2008,36(9):229-234.

[3]杨国清,张建军.控制测量学[M].第2版.郑州:黄河水利出版社,2010.

[4]何习平,陈传胜.测量技术基础[M].第2版.重庆:重庆大学出版社,2004.

[5]GB 50026—2007，中国测量规范[S].

[6]何习平.全站仪中间法与水准测量的精度比较[J].水电自动化与大坝监测,2004,28(4):37-39.

[7]余代俊.全站仪中间法代替二等水准测量的精度分析与实验[J].测绘与空间地理信息,2006,29(5):117-120.

Application of total station trigonometric levelling in soft foundation monitoring engineering

Yang Shuaidong1Qin Zaicheng2Huang Zhihuai1

(1.ZhujiangHydrologyCommunityZhujiangHydrologyScienceAcademy,Guangzhou510611,China;2.GuangdongHuananHydrologyHigh-TechDevelopmentCo.,Ltd,Guangzhou510611,China)

The thesis introduces the total station trigonometric levelling principles, analyzes major errors sources influencing the accuracy, describes the application of total trigonometric levelling in soft foundation monitoring engineering by combining with actual examples, estimates its observation accuracy, and finally points out its advantages, such as not being influenced by topography, fast construction measurement speed, and flexible operation and so on.

trigonometric levelling, mean square error of elevation difference, ball-gas difference, soft foundation monitoring

1009-6825(2016)21-0198-03

2016-05-22

杨帅东(1984- )，男，工程师；覃在诚(1994- )，男；黄志怀(1979- )，男，高级工程师

TU198

A