超磁致伸缩驱动器磁滞非线性数值模拟研究
喻曹丰,何 涛,王传礼,邓海顺,鲍 焱
(安徽理工大学 机械工程学院,安徽 淮南 232001)
超磁致伸缩驱动器磁滞非线性数值模拟研究
喻曹丰,何涛,王传礼,邓海顺,鲍焱
(安徽理工大学 机械工程学院,安徽 淮南 232001)
针对超磁致伸缩驱动器(giantmagnetostrictiveactuator,GMA)具有磁滞非线性现象,以经典Jiles-Atherton模型为基础,建立了包含偏置磁场强度和预压应力的GMA磁滞非线性模型,进行了数值仿真分析,得到了偏置磁场强度和预压应力对GMA磁化强度曲线和磁致伸缩应变曲线的影响规律。结果表明,偏置磁场强度对磁化强度曲线和磁致伸缩应变曲线的形状影响较大,调整偏置磁场强度的大小,可改变磁化强度曲线的线性区间,并能抑制或消除磁致伸缩应变曲线的倍频效应;预压应力对磁化强度曲线和磁致伸缩应变曲线的形状影响较小,施加不同的预压应力,可改变磁化强度曲线和磁致伸缩应变曲线的变化率。这与现有试验得到的结论相吻合,验证了所建磁滞非线性模型的合理性。
超磁致伸缩驱动器;磁滞非线性;磁化强度;磁致伸缩应变
0 引 言
超磁致伸缩驱动器(giantmagnetostrictiveactuator,GMA)是利用超磁致伸缩材料(giantmagnetostrictivematerial,GMM)磁致伸缩效应制作而成的一种磁-机转换器。该驱动器具有输出力大、磁-机耦合系数高、应变大、响应速度快等优异性能,在精密和超精密驱动、微定位平台以及纳米技术等领域均显示出良好的应用前景[1-3]。由于GMM具有铁磁性功能材料的磁滞效应现象,使得GMM的输入磁场和输出磁化强度之间存在磁滞非线性,导致输出位移的回程误差高达20%左右[4-5]。因此有必要建立GMA磁滞非线性模型,寻求改善其非线性的措施。
Jiles-Atherton模型是物理学家Jiles和Atherton基于铁磁材料的畴壁理论建立的磁滞模型[6],Sablik和Jiles对该模型进一步扩展,使其应用更加广泛[7]。国内外应用Jiles-Atherton模型建立磁滞模型并进行了研究。李欣欣等[8]基于Jiles-Atherton模型建立了磁滞补偿控制系统,有效消除了磁滞影响,提高了定位精度。李青峰[9]采用混合算法,实现了J-A模型的参数辨识。Dapino等[10]将Jiles-Atherton模型和二次畴转磁致伸缩模型结合,建立了描述输入电流与输出位移之间的磁滞模型。A.Nouicer等[11]提出了包含预应力的Jiles-Atherton模型,但研究偏置磁场的影响较少,也较少同时考虑偏置磁场和预压应力的影响。因此,以Jiles-Atherton模型为基础,建立包含偏置磁场强度和预压应力的GMA磁滞非线性模型并进行数值仿真分析,得到偏置磁场强度和预压应力对磁滞模型的影响规律,为改善GMA的磁滞非线性提供一种途径。
1 GMA磁场模型
GMA由底座、GMM棒、驱动线圈、永磁圆筒、外壁套筒、导磁环、预压碟簧和输出杆等部分组成,其结构示意图如图1所示。工作时,驱动线圈通入电流,驱动器内部产生磁场,GMM棒在磁场的作用下产生一定的位移和力输出,实现电磁能与机械能之间的转换。其中永磁圆筒的作用是预加一定的偏置磁场,预压碟簧的作用是给GMM棒施加一定的预压应力。

图1 GMA结构示意图
由GMA的工作原理可知,GMA工作时的磁场有如下3个来源:(1) 外加磁场Hw,包含永磁圆筒产生的磁场Hp和驱动线圈产生的磁场Hq;(2) 外加磁场使GMM棒内部磁化时产生的分子磁场Hm;(3) 预加应力诱发的磁场Hσ。
1.1外加磁场
外加磁场由永磁圆筒和驱动线圈共同产生,其中偏置磁场由永磁圆筒产生,其材料为NNF35UH型稀土铷铁硼(Nd-Fe-B),材料性能参数如表1所示。

表1 铷铁硼永磁材料性能
由铁磁体磁化理论[12]可知,均匀磁化的圆筒状永磁铁在空间任意一点的磁场可看成两个面电流密度相同,方向相反,半径分别为永磁铁内半径和外半径的单层线圈所产生磁场的矢量和,根据磁场相关计算公式,可得永磁圆筒轴线上的磁场强度Hp为
(1)
式中,Br为永磁圆筒剩磁,T;μ0为真空磁导率,取值为4π×10-7H/m;Lp为永磁圆筒的长度,m;R1p为永磁圆筒的内半径,m;R2p为永磁圆筒的外半径,m;z为永磁圆筒轴线上的点与中心位置的距离,m。
驱动线圈可认为是单层线圈在径向上叠加,而单层线圈又可认为是单匝线圈在其轴线上的叠加,可得驱动线圈轴线上磁场强度Hq为

(2)
式中,I为电流强度,A;n为轴向单位长度上的线圈匝数;n′为径向单位长度上的线圈层数;Lq为驱动线圈长度,m;R1q为驱动线圈内半径,m;R2q为驱动线圈外半径,m。
由式(1)和(2)可知,当永磁圆筒和驱动线圈的材料和结构尺寸确定时,永磁圆筒所产生的磁场强度Hp为一定值,驱动线圈所产生的磁场强度Hq与线圈匝数N和电流I有关,如式(3)Hq=fqNI
(3)
式中,fq不驱动线圈磁场系数。
则外加磁场强度Hw可表示为Hw=Hp+Hq=Hp+fqNI
(4)
1.2磁化分子磁场
根据Weiss铁磁理论[12],磁致伸缩材料在外磁场的作用下,会在其内部形成分子磁场Hm,可表示如下
(5)
式中,α为磁矩相互作用的分子场参数;M为GMM棒的磁化强度,A/m。
1.3预应力诱发磁场
已有研究表明,GMM棒内部应力的变化会对其有效磁场产生影响,并导致其磁化强度发生变化。根据Sablik和Jiles等研究成果[13-14]和热动力学理论,得出GMM棒内部的Helmholtz自由能密度为
(6)
式中,T为温度,℃;S为熵。
则包含预应力作用的有效磁场He可由自由能密度A对磁化强度M进行微分求得
(7)
假设恒温条件,温度T对磁化强度M的微分为0,则式(7)末项为0。
根据二次畴转模型[15],对于各项同性的材料,可得到磁致伸缩应变λ与磁化强度M的关系为
(8)
式中,Ms为饱和磁化强度,A/m;λs为饱和磁致伸缩系数,×10-6。
则由预加应力诱发产生的磁场强度Hσ为
(9)
即GMA内部等效磁场强度He为
(10)
2 GMA磁滞模型
获得有效磁场强度He之后,根据Boltzman统计学[16-17],可获得无磁滞磁化强度Man的Langevin模型为
(11)
式中,Ms为饱和磁化强度,A/m;a为无磁滞磁化强度形状系数。
对式(11)微分得到
(12)
根据Jiles-Atherton模型,GMM棒磁化强度M由不可逆分量Mirr和可逆分量Mrev两部分组成,其中Mirr是由物质结构的不连续性而形成的磁畴牵制引起的,Mrev是由磁畴的弹性方式弯曲引起的,可表示为
(13)
不可逆分量Mirr和可逆分量Mrev之间满足
(14)
式中,c为可逆分量系数。
则不可逆分量Mirr可表示为
(15)
磁化过程中消耗的能量可表示为
(16)
式中,k为耦合系数。
由式(14)~(16)可以得到
(17)
综合式(11)~(17)可得
(18)
式中,可逆分量系数c、畴壁相互作用系数α、无磁滞磁化强度形状系数a、不可逆损耗系数k、饱和磁化强度Ms5个参数可通过实验λ-H曲线经过参数辨识获得,在此引用A. Nouicer的参数辨识的结果[11],其值如表2所示。

表2 参数辨识结果
3 GMA磁滞模型数值分析
3.1GMA磁滞模型
综合前述建立的GMA磁滞模型,得出如下表达式
(19)
根据式(19),磁化强度M与Hq之间的关系通过MATLAB编写四阶Runge-Kutta函数进行计算,通过改变Hp和Hσ的值分析偏置磁场和预压应力对GMM磁化强度曲线和磁致伸缩应变曲线的影响规律。
3.2偏置磁场、预压应力对磁滞模型的影响
取偏置磁场Hp分别为0和20 kA/m,预压应力σ分别为0和0.4 MPa,对比分析得到,偏置磁场和预压应力对GMM磁化强度和磁致伸缩应变影响的曲线分别如图2和3所示。

图2 偏置磁场、预压应力对磁化强度的影响
Fig 2 Effect on magnetization of bias magnetic field and preloading stress
由图2和3可看出,偏置磁场对磁化强度曲线和磁致伸缩应变曲线的形状影响较大,当Hp为20 kA/m时,经计算得到,磁化强度M最大变化量为5.9×105A/m,磁致伸缩应变λ最大变化量为1140.6×10-6;预压应力对磁化强度曲线和磁致伸缩应变曲线的形状影响较小,但其各点位置处的幅值均有所增加,当σ为0.4 MPa时,磁化强度M最大变化量为5.1×104A/m,磁致伸缩应变λ最大变化量为127.69×10-6。
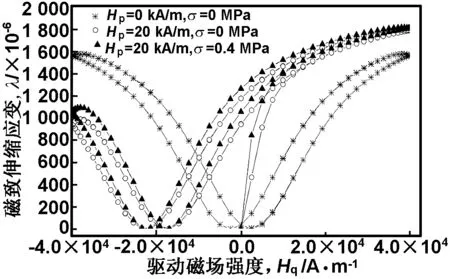
图3 偏置磁场、预压应力对磁致伸缩应变的影响
Fig 3 Effect on magnetostrictive strain of bias magnetic field and preloading stress
3.3偏置磁场强度对磁滞模型的影响
取偏置磁场强度Hp分别为0,20,40和50 kA/m,分析得到磁化强度M、磁致伸缩应变λ与驱动磁场强度Hq的关系曲线分别如图4和5所示。

图4 偏置磁场对磁化强度的影响
Fig 4 Effect on magnetization of bias magnetic field

图5 偏置磁场对磁致伸缩应变的影响
Fig 5 Effect on magnetostrictive strain of bias magnetic field
由图4可看出,当偏置磁场强度为0时,磁化强度曲线与驱动磁场强度在[-20,20 kA/m]区间内近似成线性关系,当偏置磁场强度发生改变时,此线性关系的区间会随之发生变化;由图5可看出,当偏置磁场强度为0时,磁致伸缩应变曲线的机械周期是驱动磁场周期的一半,即其频率是驱动磁场频率的两倍,通常称之为“倍频效应”,且随着偏置磁场强度的增大,这种“倍频效应”会受到抑制,当偏置磁场强度为20 kA/m时,其频率是驱动频率的1.5倍,当偏置磁场强度为40 kA/m时,其频率与驱动频率相等,“倍频效应”消失。这与A.Lovisolo等[18]等通过试验得出的结论相吻合。
因此,选择合适的偏置磁场强度对改变磁化强度曲线的线性区间和抑制磁致伸缩应变曲线的“倍频效应”均具有显著的效果。
3.4预压应力对磁滞模型的影响
取预压应力分别为0,1,1.5和2 MPa,分析得到磁化强度M、磁致伸缩应变λ与驱动磁场强度Hq的关系曲线分别如图6和7所示。
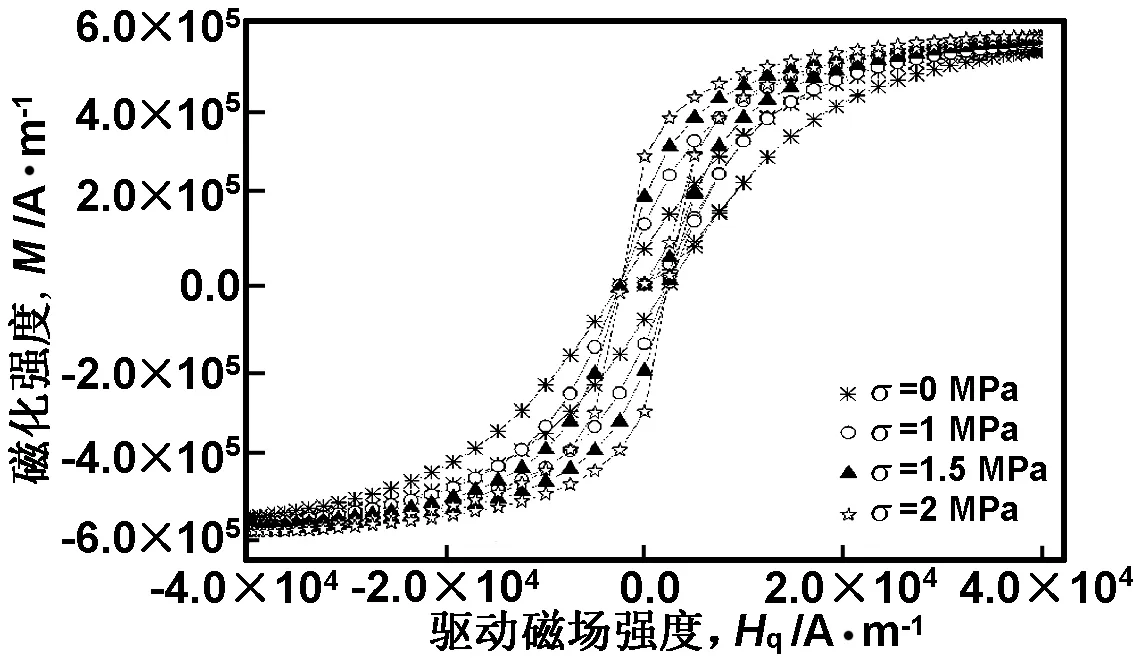
图6 预压应力对磁化强度的影响
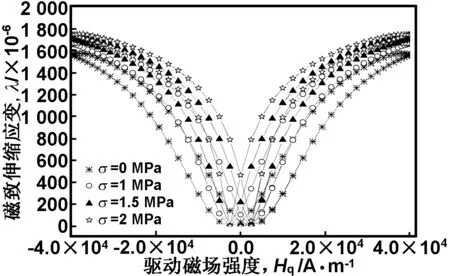
图7 预压应力对磁致伸缩应变的影响
Fig 7 Effect on magnetostrictive strain of preloading stress
由图6和7可看出,随着预压应力的增大,磁化强度曲线和磁致伸缩应变曲线的变化率均随之增大,以驱动磁场强度Hq为0 kA/m位置处,计算磁化强度曲线的变化率;以驱动磁场强度为5 kA/m位置处,计算磁致伸缩应变曲线的变化率,结果分别如表3所示。由表3可得,随着预压应力σ的增大,磁化强度曲线的变化率kM随之增大,单位兆帕的平均增幅约为52.62%,但增长幅度随之缓慢降低,磁致伸缩应变曲线的变化率kλ也随之增大,单位兆帕的平均增幅约为1.17,且增长幅度也随之降低。这与O.Bottauscio等[19]通过试验得出的结论相吻合。
因此,预压应力可改变磁化强度曲线和磁致伸缩曲线的变化率,选择合适的预压应力能够适应具有不同磁化强度和磁致伸缩应变变化率需求的应用场合。
表3预压应力对磁化强度和磁致伸缩应变的影响
Table 3 Effect on magnetization and magnetostrictive strain of preloading stress

预压应力σ/MPa011.52磁化强度变化率kM(Hq=0kA/m)33.1252.5166.6981.80kM增长幅度/%58.5454.0145.31磁致伸缩应变变化率kλ(Hq=5kA/m)0.0290.0720.1150.163kλ增长幅度1.481.190.83
4 结 论
以经典Jiles-Atherton模型为基础,建立了包含偏置磁场强度Hp和预压应力σ的GMA磁滞非线性模型,并利用MATLAB进行了数值模拟分析,得出如下结论:
(1)偏置磁场强度对磁化强度曲线形状影响较大,当偏置磁场强度为20 kA/m时,其磁化强度M最大变化量为5.9×105A/m;且通过改变偏置磁场强度的大小,可改变磁化强度曲线的线性区间。
(2)偏置磁场强度对磁致伸缩应变曲线的形状影响较大,当偏置磁场强度为20 kA/m时,磁致伸缩应变λ最大变化量为1140.6×10-6;且通过选择合适的偏置磁场强度,可抑制或消除磁致伸缩应变曲线的“倍频效应”。
(3)预压应力对磁化强度曲线形状影响较小,当预压应力为0.4 MPa时,其磁化强度M最大变化量为5.1×104A/m;且随着预压应力增大,磁化强度曲线的变化率随之增大,单位兆帕的平均增幅约为52.62%,但增长幅度随之缓慢降低。
(4)预压应力对磁致伸缩应变曲线的形状影响较小,当预压应力为0.4 MPa时,其磁致伸缩应变λ最大变化量为127.69 ×10-6;且随着预压应力的增大,磁致伸缩应变曲线的变化率随之增大,单位兆帕的平均增幅约为1.17,但增长幅度随之降低。
[1]Wang Bowen, Cao Shuying, Huang Wenmei. Magnetostrictive materials and devices [M]. Beijing: Metallurgical Industry Press, 2008:174-175.
王博文,曹淑瑛,黄文美.磁致伸缩材料与器件[M].北京:冶金工业出版社,2008:174-175.
[2]Wang Bin, Qu Wentai, Wu Yijie, et al. Review on hysteretic modeling of giant magnetostrictive materials [J]. Journal of Functional Materials, 2013, 44(16):2295-2300.
王彬,屈稳太,邬义杰,等.超磁致伸缩材料磁滞建模方法国内外研究现状评述[J].功能材料,2013, 44(16):2295-2300.
[3]Zhu Yuchuan, Li Yuesong. A novel jet pipe servo valve driven by giant magnetostrictive actuator [J]. Piezoelectrics & Acoustooptics, 2010, 32(4):574-577.
朱玉川,李跃松.超磁致伸缩执行器驱动的新型射流伺服阀[J].压电与声光,2010,32(4):574-577.
[4]Jia Zhenyuan, Wang Fuji, Guo Dongming. Functional material driving microactuator and its key technology [J]. Chinese Journal of Mechanical Engineering, 2003,39(12):61-67.
贾振元,王福吉,郭东明. 功能材料驱动的微执行器及其关键技术[J].机械工程学报, 2003,39(12):61-67.
[5]Liu Huifang, Jia Zhenyuan, Wang Fuji, et al. Para meter iden tification of displace ment model for giant magnetostrictive actuator[J]. Journal of Mechanical Engineering, 2011, 47(15):115-120.
刘慧芳,贾振元,王福吉.超磁致伸缩执行器位移模型的参数辨识[J].机械工程学报,2011,47(15):115-120.
[6]Jiles D C,Atherton D L. Ferromagnetic hysteresis[J]. IEEE Transactions on Magnetics,1983,19(5):2183-2185.
[7]Sablik M J,Jiles D C. A model for magnetostriction hysteresis[J]. J Appl Phys,1988,64(10):5402-5404.
[8]Li Xinxin, Wang Wen, Chen Jianheng, et al. Hysteresis compensation of giant magnetostrictive actuator based on Jiles-Atherton model [J]. Optics and Precision Engineering, 2007,15(10):1558-1563.
李欣欣,王文,陈戬恒,等. Jiles-Atherton模型的超磁致伸缩驱动器磁滞补偿控制[J]. 光学精密工程,2007,15(10):1558-1563.
[9]Li Qingfeng. Achievement of J-A hysteresis model based on a hybrid algorithm [D]. Beijing: North China Electric Power University,2010.
李青峰. 基于混合算法的J-A磁滞模型的实现[D]. 北京:华北电力大学,2010.
[10]Dapinoo M J, Smith R C, Flatau A B. Structural magnetic strain model for magnetostrictive transducers[J]. IEEE Transactions on Magnetics,2000,36 (3):545-556.
[11]Nouicer A,Nouicer E, Mahtali M,et al. A Neural network modeling of stress behavior in nonlinear magnetostrictive materials[J]. J Supercond Nov Magn,2013, 26:1489-1493.
[12]Dai Daosheng, Qian Kunming. The ferromagnetics (volume 1)[M]. Beijing: Science Press,1987:114.
戴道生,钱昆明.铁磁学(上册)[M].北京:科学出版社,1987:114.
[13]Jiles D C,Thoelke J B,Devine M K. Numerical determination of hysteres is parameters for the modeling of magnetic properties using the theroy of ferromagnetic hysteresis [J]. IEEE Transactions on Magnetics,1992,28 (1):27-35.
[14]Sablik M J,Kwun H,Burkhardt G L,et al. Modeling for the effect of tensile and compressive stresson ferromagnetic hysteresis [J]. J Appl Phys,1987,61(8):3799-3801.
[15]Jia Zhenyuan, Wang Fuji, Zhang Ju, et al. Hysteresis nonlinearity modeling and control of giant magnetostrictive actuator [J]. Chinese Journal of Mechanical Engineering, 2005,41(7): 131-135.
贾振元,王福吉,张菊,等.超磁致伸缩执行器磁滞非线性建模与控制[J].机械工程学报,2005,41(7):131-135.
[16]Cao Shuying. Dynamic model with hysteresis nonlinearity and control technique for giant magnetostrictive actuator[D]. Tianjin: Hebei University of Technology, 2004.
曹淑瑛. 超磁致伸缩致动器的磁滞非线性动态模型与控制技术[D]. 天津:河北工业大学, 2004.
[17]Sablik M J, Jiles D C. Coupled magnetoelastic theory of magnetic and magnetostrictive hysteresis[J].IEEE Trans Magn,1993, 29(3):2113-2123.
[18]Lovisolo A, Roccato P E, Zucca M. Analysis of a magnetostrictive actuator equipped for the electromagnetic and mechanical dynamic characterization [J].Journal of Magnetism and Magnetic Materials,2008,320(20):915-919.
[19]Bottauscio O,Lovisolo A,Roccato P E,et al.Modeling and experimental analysis of magnetostrictive devices: from the material characterization to their dynamic behavior [J]. IEEE Transactions on Magnetics,2008,44(11): 3009-3012.
Numericalsimulationresearchonhysteresisnonlinearofgiantmagnetostrictiveactuator
YUCaofeng,HETao,WANGChuanli,DENGHaishun,BAOYan
(CollegeofMechanicalEngineering,AnhuiUniversityofScienceandTechnology,Huainan232001,China)
Aimingatthephenomenononthehysteresisnonlinearityofgiantmagnetostrictiveactuator(GMA),basedontheclassicalJiles-Athertonmodel,ahysteresisnonlinearmodelisestablisedcontainingbiasmagneticfieldintensityandpreloadingstressofGMA.ThelawofGMAmagnetizationcurvesandmagnetostrictivestraincurvesareobtainedrespectivelyaboutbiasmagneticfieldintensityandpreloadingstressbynumericalsimulationanalysis.Analysisresultsshowthatmagnetizationcurveandmagnetostrictivestraincurveareinfluencedgreatlybythebiasmagneticfieldintensityatshape,andthatthelinearrangeofthemagnetizationcurvecanbechangedandthefrequencydoublingeffectofmagnetostrictivestraincurvecanberestrainedoreliminatedbyadjustingthesizeofthebiasmagneticfieldintensity,andthatthemagnetizationcurveandmagnetostrictivestraincurveshapeareaffectedbypreloadingstress,andthatwiththeincreaseofpreloadingstress,therateofchangeofmagnetizationcurveandmagnetostrictivestraincurveareincreasingandtheamplitudewerereducedslowly.Thehysteresisnonlinearitymodelisreasonablebeacusetheseconclusionsareconsistentwiththeexperiments.
giantmagnetostrictivematerial;hysteresisnonlinearity;magnetization;magnetostrictivestrain
1001-9731(2016)05-05170-06
国家自然科学基金资助项目(51075001,51205002);安徽省科技计划资助项目(1301022074)
2015-11-10
2016-01-10 通讯作者:王传礼,E-mail:Chlwang@aust.edu.cn
喻曹丰(1987-),男,安徽安庆人,在读博士,师承王传礼教授,从事智能材料及其控制技术研究。
TP273
A
10.3969/j.issn.1001-9731.2016.05.032

