循环水中不锈钢缝隙腐蚀数值模拟研究

文　博

(西安石油大学机械工程学院，陕西　西安　710065)



循环水中不锈钢缝隙腐蚀数值模拟研究

文博

(西安石油大学机械工程学院，陕西西安710065)

采用Comsol有限元软件对316L不锈钢在循环水溶液中一维稳态缝隙腐蚀过程进行了数值计算与模拟。求解域求解的控制方程包含了电迁移、对流、扩散等过程，电极反应动力学采用的阳极塔菲尔关系式，计算了电势分布、氯离子浓度及pH分布。计算出的pH与氯离子浓度的分布规律与文献值趋势接近。本研究还模拟了本体溶液不同的初始pH值和氯离子浓度对缝隙内离子浓度与pH分布的影响。本模拟研究的结果为接下来缝隙内闭塞区的研究提供了依据。

316L不锈钢；缝隙腐蚀；数值模拟

在管壳式换热器中，管子、管板与焊缝之间的狭小缝隙，由于氧气扩散受阻，形成“大阴小阳”，然后缝隙内的自催化作用使缝隙内的pH不断降低，导致钝化膜破裂引起缝隙腐蚀。本文假设反应界面处于活化状态，利用Comsol软件模拟了316L在循环水中的缝隙腐蚀过程，计算了缝隙内的pH与氯离子分布，研究结果有助于接下来对缝隙内部多种金属的组合进行研究。

1　计算模型

模型建立在金属腐蚀反应、平衡反应及其扩散、电荷平衡的基础上。缝隙内的九个主要反应为阳极主要金属的溶解反应及一次水解平衡反应和二次水解平衡反应。

1.1几何模型

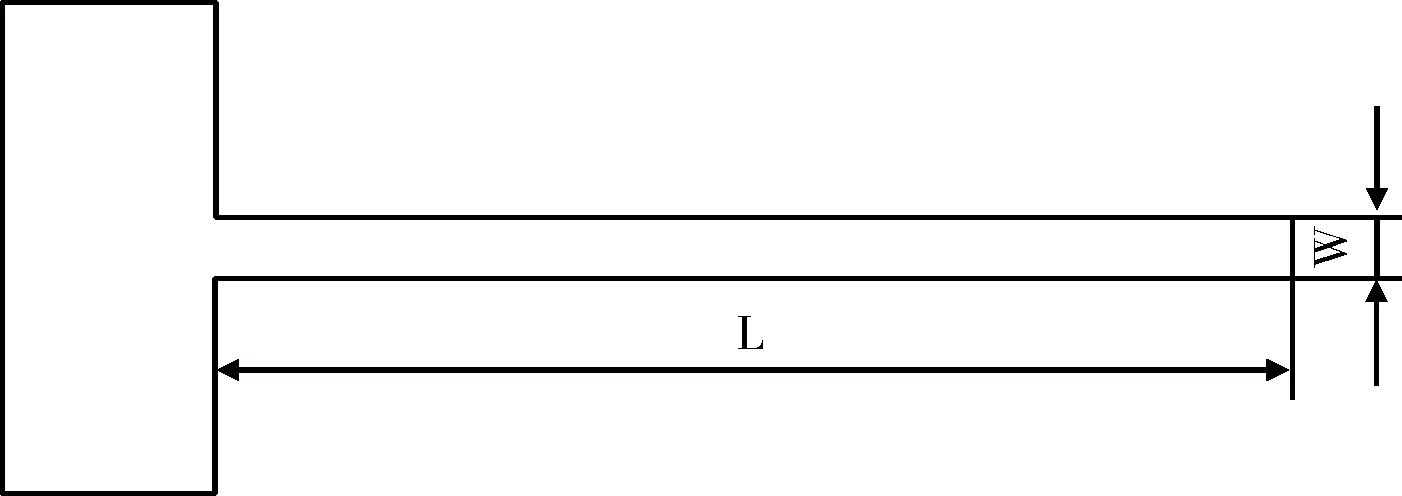
图1　模拟模型

我们通常将金属间的狭长缝隙作为缝隙腐蚀的研究对象，并且假设缝隙的长度远远大于缝隙的深度。参考Abdulsalam[1]运用Comsol软件模拟铁在醋酸中的缝隙腐蚀采用的一维模型，所以本文几何模型采用L=5 cm W=3 mm的一维模型。

1.2模型假设

(1) 缝隙内溶液处于稳态;

(2) 忽略溶液中的气相和固相;

(3) 假设缝隙内的化学反应达到平衡;

(4) 忽略不锈钢其他杂质组分对腐蚀速率的影响;

(5) 只考虑阳极电化学反应和金属离子的二次水解。

1.3控制方程

缝隙内离子的摩尔通量计算如下：

Ni=-Di▽Ci-uiziCiF▽V

(1)

式中：Ni——第j种离子的摩尔通量，mol/m3·s

Ci——离子的浓度，mol/m3

V——溶液静电势，V

Di——离子扩散系数，m2/s

zi——离子电荷数

ui——离子迁移系数，s·mol·kg-1

F——法拉第常数，C·mol-1

方程(1)由两部分组成：第一部分是由浓度梯度作用下的扩散通量，第二部分由电势梯度作用下的电迁移通量。

溶液中电流：

(2)

物质j的迁移率可通过Nernst-Einstein方程计算：

式中：n——单位体积载流子数

K——玻尔兹曼常数

q——载流子电荷量

D——扩散系数

由上式计算得：

(3)

根据泊松方程，电势可以表示为：

(4)

式中：ε0——溶液真空介电常数，F·m-1

εr——溶液相对介电常数，F·m-1

根据质量守恒，整个体系可以表示为：

(5)

式中：Rj——包含产生和消耗的化学反应速率

将式(1)(2)(4)代入式(5)可得nernst-planck方程的一般形式：

(6)

溶液满足电中性条件：

(7)

1.4电化学反应与水解反应

此模型根据316L不锈钢的实际成分，假设模型中的不锈钢成分为：72%Fe，18%Cr，10%Ni，不考虑其他杂质。所以缝隙内主要的阳极反应如下：

(8)

(9)

(10)

电极反应动力学表达式类型为阳极Tafel方程：

(11)

式中：Iloc——电流密度

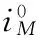
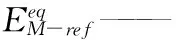
bM——金属氧化反应的Tafel斜率

总的阳极反应表达式为：

i总=0.732×iFe+0.192×iCr+0.076×iMi

式中：i总——阳极电流密度

水解反应

二次水解

水解方程：

(12)

式中：Keq——平衡常数

ci——物质浓度

ca0——单位活性浓度

νi——化学计量系数

1.5边界条件

由于采用一维模型，所以边界条件只有主体溶液边界、无通量边界、绝缘边界。

对于主体溶液边界，浓度和电势均为定值。

ci=c0

(13)

φ=φbnd

(14)

对于绝缘边界，电势梯度为零。

n·i=0

(15)

对于无通量边界，浓度梯度为零。

n·Ni=0

(16)

2　结果与讨论

本文计算了缝隙宽度W=0.3 mm，长度L=5 cm的模型，缝口电位设定为V=-1.7 V(SCE)。假设孔内壁面处于活化腐蚀状态，忽略了缝隙外部的阴极反应。

2.1氯离子浓度曲线

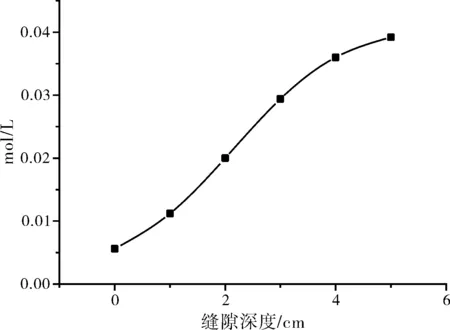
图2　氯离子浓度分布曲线

如2所示，越到缝隙底部，氯离子浓度越高。缝隙底部氯离子浓度最高，达到0.0392 mol/L，是本体溶液氯离子浓度(0.0056 mol/L)的7倍。符合Fontana[2]报导的氯离子浓度在缝隙底部浓集约3～10倍。

2.2pH分布曲线

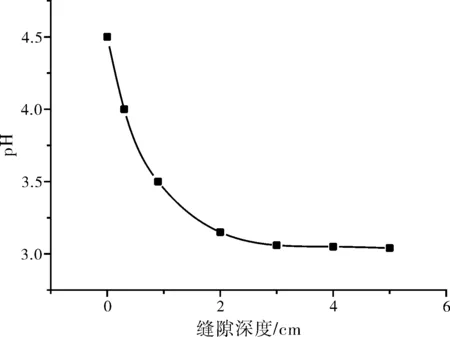
图3　缝隙内pH分布曲线

研究结果表明，pH值随着缝隙深度的增加而降低，缝隙口下降最快，缝隙底部pH值最低(pH=3)。本研究模型计算的pH曲线与刘东鹏[3]、王巍等[4]计算的pH值曲线具有相同的变化趋势，符合左景伊[5]的理论。pH下降趋势变缓，可能是由于金属离子的水解达到极限值。

电势分布曲线

图4　电势分布曲线

图4给出了电势在缝隙内部的分布情况。随着缝隙深度的增加，电位逐渐降低，在孔口位置电势梯度较大，缝隙底部曲线平缓。电位降约为30 mV。本模型计算的电势分布趋势与实验趋势数据吻合。

2.3氯离子浓度对pH的影响

本模型模拟了不同浓度氯离子浓度下的pH(图5)，结果显示，随着本体溶液氯离子浓度的增加，缝隙底部pH变低。如图5所示,0.0102 mol/L氯离子浓度下，缝隙底部pH最低，0.0056 mol/L氯离子浓度下，缝隙底部pH最高。LEE等[6]的研究结果表明，本体溶液中氯离子浓度的增加会加速碳钢缝隙内pH的变化并且产生更加酸化的环境。本模型的结果表明了，316L不锈钢在循环水溶液中也具有相同的结论。pH的降低可能是由于氯离子浓度增大，导致腐蚀电位下降，加速腐蚀，进而导致pH下降。

图5　不同氯离子浓度下的pH分布

2.4pH对氯离子分布的影响

本模型模拟了不同pH下的氯离子迁入量，结果显示，pH越低，在缝隙底部氯离子浓集越多。pH=5时缝底的浓度是孔口的8.5倍，pH=6时，大约是8倍，pH=7时，是7倍。氯离子浓度的增加可能是由于本体溶液中的pH下降，或多或少影响了缝隙内部的pH(降低)，加速阳极溶解，因为电中性，更多的氯离子聚集到了缝隙底部。

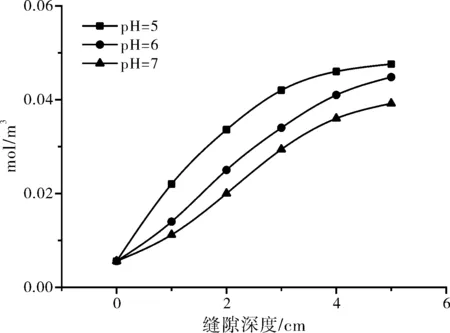
图6　不同pH下氯离子的迁入量

2.5孔口电位对孔底pH值的影响

本模型还模拟了不同孔口电位下的pH(图7)，如图7所示，孔口电位为-1.7 V(SCE)时，缝底pH约为3，当孔口电位降到-1.9时，pH升至4。结果表明，随着孔口电位的降低，pH升高。与刘东鹏[3]的模拟结论相符。

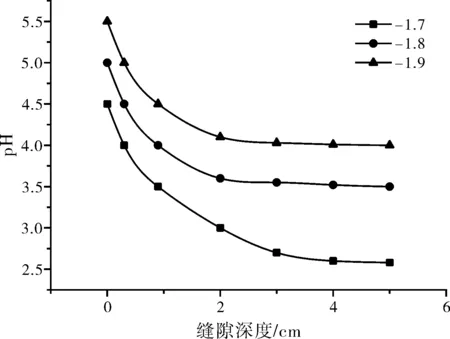
图7　不同孔口电位下的pH曲线

3　结　论

(1) 采用Comsol软件模拟了316L不锈钢在循环水中的缝隙腐蚀过程。得到了其活化腐蚀状态下缝隙内的氯离子浓度、pH、电势分布。为模拟循环水缝隙中闭塞区的溶液提供了依据。

(2) 计算了不同氯离子浓度下缝隙内部的pH分布。结果表明，氯离子浓度越高，缝隙底部pH越低。pH的降低可能是由于氯离子浓度增大，导致腐蚀电位下降，加速腐蚀，进而导致pH下降。

(3) 计算了不同pH下氯离子的浓集。结果表明，pH越低，缝隙底部氯离子浓集度越大。氯离子浓度的增加可能是由于本体溶液中的pH下降，或多或少影响了缝隙内部的pH(降低)，加速阳极溶解，因为电中性，更多的氯离子聚集到了缝隙底部。

[1]Abdulsalam,Mohammed.Determining the Critical Crevice Depth for Iron in a Sodium Acetate-Acetic Acid Buffer Solution[J].Electrochemical Society,2003,9.

[2]FONTANA M G, GREENE N D. Corrosion Engineering [M]. New York: Mc Graw2Hill Book Company,1978.

[3]刘东鹏,王亚飞,程光旭.奥氏体不锈钢缝隙腐蚀的数值模拟研究[J].腐蚀与防护,2012,10(2):72-76.

[4]王巍.几种金属在海水中阴极保护数值计算及瞬态激励影响研究[D].2011.

[5]左景伊,金志强.腐蚀裂缝内化学和电化学状态之探索-氯离子迁入量和pH的相互关系[J].化工学报,1982(4):291-300.

[6]YH.Lee,Z.Takehara,S.Yoshizawa.The enrichment of hydrogen and chloride ions in the crevice corrosion of steels[J].Corrosion Seienee,1981,21(5):391-397.

[7]刘幼平,周培君,张洁.外部电位对蚀孔或裂缝扩展阶段闭塞区腐蚀行为的影响[J].中国腐蚀与防护学报,1995,15(1):43-48.

[8]Oldfield J W,Sutton W H.Crevice corrosion of stainless steels I:A mathematical model[J].British Corrosion Journal,1978,13(1):13-22.

Crevice Corrosion Numerical Simulation Study of Stainless Steel in the Circulating Water

WENBo

(Institute of Mechanical Engineering,Xi’an Petroleum University, Shaanxi Xi’an 710065,China)

The finite element software Comsol was used for the numerical calculation and simulation to 316L stainless steel in aqueous solution of one-dimensional steady-state crevice corrosion process.The governing equation contained the domain to solve electric migration, convection and diffusion process of electrode reaction kinetics of anode tafel equation, to calculate the electric potential distribution, chlorine ion concentration and pH distribution.The pH and chlorine ion concentration distribution was calculated and trend was close to literature values.This study also simulates the bulk solution with different initial pH and chlorine ion concentration within the cracks on the distribution of the ion concentration and pH.The simulation results for the following research provided a basis in gap within the block.

316L stainless steel;crevice corrosion;numerical simulation

TE986

A

1001-9677(2016)03-0095-04