抗简单功耗攻击的SM2原子算法

韩晓薇　乌力吉　王蓓蓓　王　安

(清华大学微电子学研究所　北京　100084)



抗简单功耗攻击的SM2原子算法

韩晓薇乌力吉王蓓蓓王安

(清华大学微电子学研究所北京100084)

(hanxiaoweihxw@gmail.com)

SM2算法是中国国家密码管理局颁布的商用椭圆曲线公钥密码标准算法.传统密码算法通常存在安全漏洞，攻击者往往针对算法中的安全薄弱环节展开攻击，分析提取密钥，对密码系统和人们的财产安全构成很大威胁.功耗攻击是最常见的攻击方式，它具有较小密钥搜索空间及较高分析效率等诸多优点.功耗攻击利用密码算法运行过程中的功耗泄漏，采集功耗曲线分析恢复得到密钥.为有效抵抗功耗攻击，提高SM2算法安全性，参考国际椭圆曲线密码算法，将原子概念运用到SM2中，提出一种新型结构的原子算法.经理论分析，在运算量方面相比基本算法降低了27.4%，并且均低于已有的原子算法.经由SAKURA-GFPGA仿真验证结果表明，能够成功抵抗简单功耗攻击.

SM2算法；密码系统；功耗攻击；椭圆曲线密码算法；原子算法

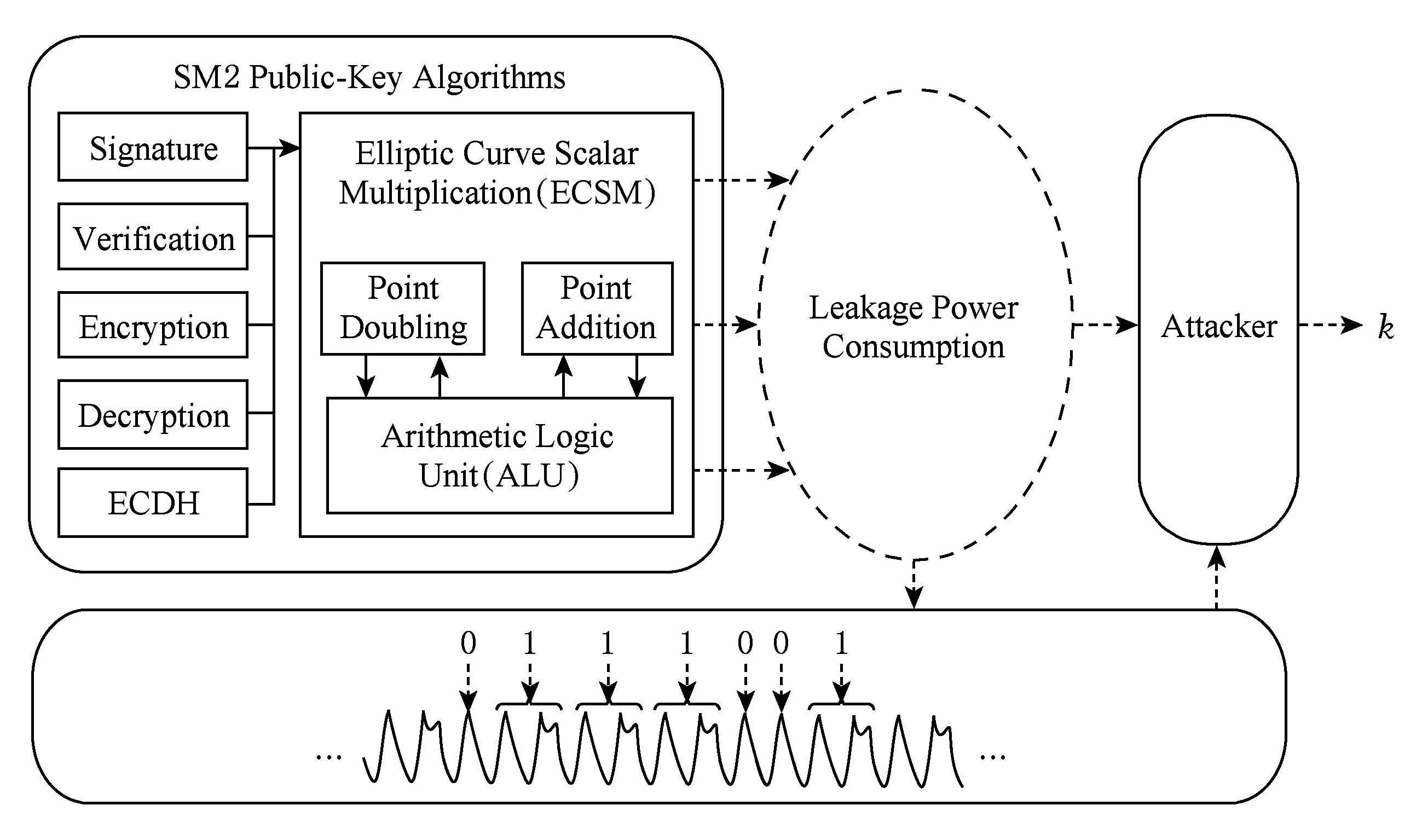
Fig. 1　Architecture of SM2 algorithms.图1　SM2算法结构图

椭圆曲线密码体制[1-2]自1985年被提出以来在理论探究和实际应用方面均逐渐成为研究的重点.相比传统公钥加密算法RSA，椭圆曲线密码体制安全性高、计算速度快、存储空间小、带宽要求低、计算参数少且签名短小，更加适用于限制资源的系统.在商用密码领域，中国不断推出自主定义的密码算法.2010年，国家密码管理局公布了SM2椭圆曲线公钥密码标准算法[3].经各方不断研究论证，SM2目前已应用于多种商用密码通用产品中，并有望与其他国密算法一起登上国际密码舞台.

传统密码攻击按攻击主动性可分为侧信道攻击和故障攻击两大类[4-5].侧信道攻击通常被称为被动攻击，攻击者通过采集密码运算过程中泄露的侧信道信息恢复密钥.故障攻击则通过人为注入故障(如时钟毛刺、电压毛刺等)，利用错误结果恢复密钥.侧信道攻击包含功耗攻击与电磁攻击，其中功耗攻击具有较小密钥搜索空间和较高分析效率，是目前攻击者们最常采用的攻击方式，对商用智能卡芯片安全构成很大威胁.随着国家由磁条卡向芯片卡计划的不断推进，研究SM2算法的抗功耗攻击能力对于金融安全意义重大.

SM2包含加密、解密、签名、验签和密钥交换5部分，其中多次涉及标量乘操作.标量乘又称点乘，即为给定椭圆曲线上的一点P与整数d，求取多倍点dP.标量乘的逆运算是已知P与dP，求取标量d，此即为求解椭圆曲线离散对数问题(ECDLP).该过程计算复杂度很高，从而保证了SM2算法的安全性.

现有攻击方式大多针对标量乘，致力于不依靠求解ECDLP而恢复d.标量乘运算的中间过程涉及大量逻辑门的翻转，不同的步骤会呈现不同的功耗.简单功耗攻击(simplepowerattack，SPA)[6]是最早提出的一种攻击，它通过分析SM2运算过程中泄露的功耗信息得到点加(pointaddition)与倍点(pointdoubling)的执行规律，只需1条功耗曲线即可恢复密钥.2004年，Chevallier-Mames等人[7]提出侧信道原子算法的概念，其原理是将公钥算法的中间过程分解为具有相同运算规律的原子块，从而将功耗曲线平均化，能够在不增加开销的条件下成功抵抗SPA.

本文将原子算法的概念运用到SM2算法中，结合SM2的特殊性，在前人基础上改进优化中间算法，旨在为抗SPA提供多种思路，最后与已有抗SPA的算法进行对比.

1　背景介绍

1.1SM2算法及功耗攻击

SM2公钥密码算法体系中签名与解密因与私钥有关而成为攻击与防护的重点.5部分算法中都包含椭圆曲线标量乘，标量乘由大量椭圆曲线倍点与点加组成，其包含关系如图1所示：

功耗攻击利用密码算法运算过程中的功耗泄漏恢复密钥.密码芯片属于特殊的数字电路，数字电路由大量晶体管组成，晶体管的翻转会影响功耗变化.总的来说，密码芯片的功耗由4部分组成：与密码运算相关的晶体管翻转产生的功耗、与密码运算无关的晶体管翻转产生的功耗、漏电流产生的功耗和噪声功耗.由此可见，密码芯片的功耗与算法运算的指令和数据密切相关，这为功耗攻击提供了可能.目前已有多种功耗攻击方式：SPA、差分功耗攻击(differentialpowerattack，DPA)[8]、相关功耗攻击(correlationpowerattack，CPA)等.

标量乘决定着SM2算法的性能及安全性，多种快速算法及安全防护对策被相继提出.但是，大多数安全对策均在不同程度上增加了运算量，研究不增加运算量的安全对策意义重大.最基本标量乘算法是二进制扩展法，将标量d用二进制表示，从左至右或从右至左依次判断每一位，若为0则执行1次倍点，为1执行1次倍点与1次点加，如算法1所示.

算法1. 二进制扩展法.

输入：d=(dn-1,dn-2,…,d1,d0)2，P∈E(Fq)；

输出：Pd=dP.

① Q0←∞，Q1←P；

② 对于i从n-1到0重复执行

Q0←2Q0；

若di,=1,则Q0←Q0+Q1；

③ 返回Q0.

采用算法1，攻击者利用点加与倍点功耗的不同，只需1条功耗曲线便可观察出操作规律，进而得到密钥，此即为SPA，如图1所示.

之后，Coron提出总执行倍点与点加(double-and-addalways)算法[9]，该算法在di=0时添加冗余操作，保证无论di是0或1均执行1次倍点和1次点加，如算法2所示.如此可抵抗SPA，但同时增加了一倍的点加，大大增加了运算量.

算法2. 总执行点加与倍点法.

输入：d=(dn-1,dn-2,…,d1,d0)2，P∈E(Fq)；

输出：Pd=dP.

① Q0←∞，Q2←P；

② 对于i从n-1到0重复执行

Q0←2Q0；

Q1←Q0+Q2；

若di=1,则Q0←Q0；

否则Q0←Q1；

③ 返回Q0.

侧信道原子算法[7,10-11]的概念将密码算法表示为原子结构，使得算法执行过程中循环处理相同的指令原子块，如此功耗曲线呈现相同规律变化，能够成功抵抗SPA.

1.2SM2点加倍点介绍

设域K的特征为2或3，SM2使用定义在域K上的椭圆曲线y2= x3-3x+b.对这条曲线而言，倍点与点加(2个互不相同且互不为负的点相加)运算需要用到域上的求逆与乘法，而求逆操作比乘法耗费大量时间，因此将运算转化到投影坐标系是常用的解决方法.其中，雅可比坐标下的倍点计算速度最快，雅可比与仿射混合坐标下的点加计算速度最快.

倍点：将椭圆曲线转化到仿射坐标系下，然后利用仿射坐标形式的倍点公式计算2P，消去分母后得到雅可比坐标形式的计算公式：

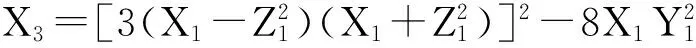
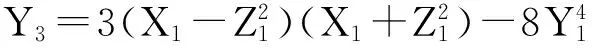
(1)

由式(1)可知，通过4次域的平方和4次域的乘法能够计算出X3，Y3，Z3.

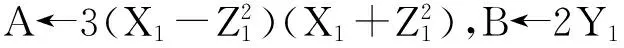
C←B2，D←CX1，X3←A2-2D，

Y3←A(D-X3)-C22，Z3←BZ1.

点加：将椭圆曲线转化到仿射坐标系下，令P=(X1:Y1:Z1)∈E，Z1≠0，Q=(X2:Y2:1)，假设P≠±Q.利用仿射坐标形式的点加公式计算P+Q，消去分母后得到雅可比坐标形式的计算公式：

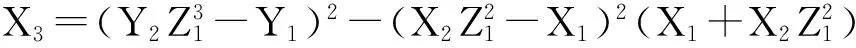
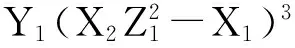
(2)

由式(2)可知，通过3次域的平方和8次域的乘法能够计算出X3，Y3，Z3.

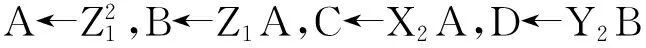
E←C-X1，F←D-Y1，G←E2，H←GE，

I←X1G，X3←F2-(H+2I)，

Y3←F(I-X3)-Y1H，Z3←Z1E.

上述点加公式中，Q为固定点，若Q为非固定点(X1:Y1:Z1)，则需要4次域的平方和12次域的乘法.

2　改进的原子算法

实际实现中模平方通常用模乘代替.Chevallier-Mames等人[7]的方案中，原子块为MUL-ADD-REV-ADD结构，即模乘-加法-求反-加法.本文将原子概念与SM2结合，调整寄存器运算顺序，把点加倍点均表示为模乘-加法-减法(MUL-ADD-SUB)结构的指令原子块.

如图2所示，传统算法根据di不同执行不同指令，令Π0代表倍点，Π1代表点加.改进算法将Π0与Π1用统一的原子块Г表示，Г包含1次模乘、1次加法和1次减法，适用于雅可比坐标系下的标量乘.

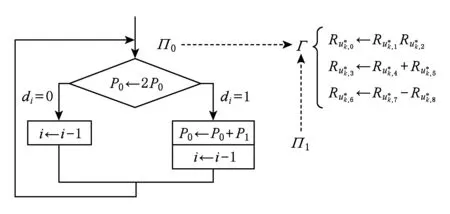
Fig. 2　Atomic structure of scalar multiplication.图2　标量乘原子结构示意图

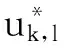
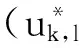
算法3. 原子标量乘算法.

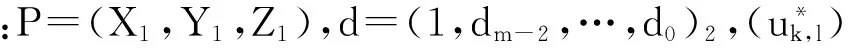
输出：Pd=dP.

R0←X1，R1←Y1，R2←Z1，R6←X1，R7←Y1；

i←m-2，s←1.

① 对于i≥0重复执行：

k←(s)(k+1)；

s←di(kdiv18)+(di)(kdiv7)；

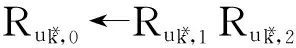
i←i-s；

② 返回(R1,R2,R3).

P为非固定点时，点加需16次模乘，算法3中的s替换为di(kdiv23)+(di)(kdiv7)，寄存器下标矩阵取)0≤k≤230≤l≤8.考虑到此时倍点需8次循环，点加需16次循环，二者均为8的倍数，变换算法如算法4所示.在循环内部嵌套1个周期为8的for循环，设for循环为原子块Γ ′，通过k与s控制i的变化，di=0时执行1次Γ ′，di=1时执行3次Γ ′，即倍点执行1次Γ ′，点加执行2次Γ ′.如此，可在具有相同安全性的基础上节省多次计算k，s和i的操作，进一步降低计算量.

算法4. 改进原子标量乘算法.

输出：Pd=dP.

R0←X1，R1←Y1，R2←Z1，R6←X1，R7←Y1；

i←m-2，s←1.

① 对于i≥0重复执行：

s←di(kdiv16)+(di)；

对于j从0至7重复执行：

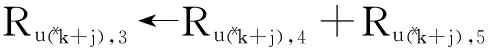
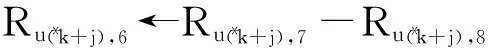
j=j+1；

i←i-s；

② 返回(R1,R2,R3).

3　性能评估

3.1安全性分析

传统SM2算法中，攻击者很容易通过观察功耗波形得到点加与倍点的运算规律，进而推算密钥.本文将原子概念运用到SM2算法中，把SM2中的点加与倍点用相同的原子块表示，执行点加和倍点时功耗波形将不再存在差别，攻击者无法得到运算规律，能够成功抵抗SPA.

为了验证该方案的安全性，本文基于传统算法与所提方案分别进行电路设计实现，并在如图3所示的SAKURA-G开发板上成功验证.开发工具为ISEDesignSuite14.4，FPGA型号为XilinxSpartan-6 (XC6SLX75-2CSG484C)，时钟频率为48MHz.

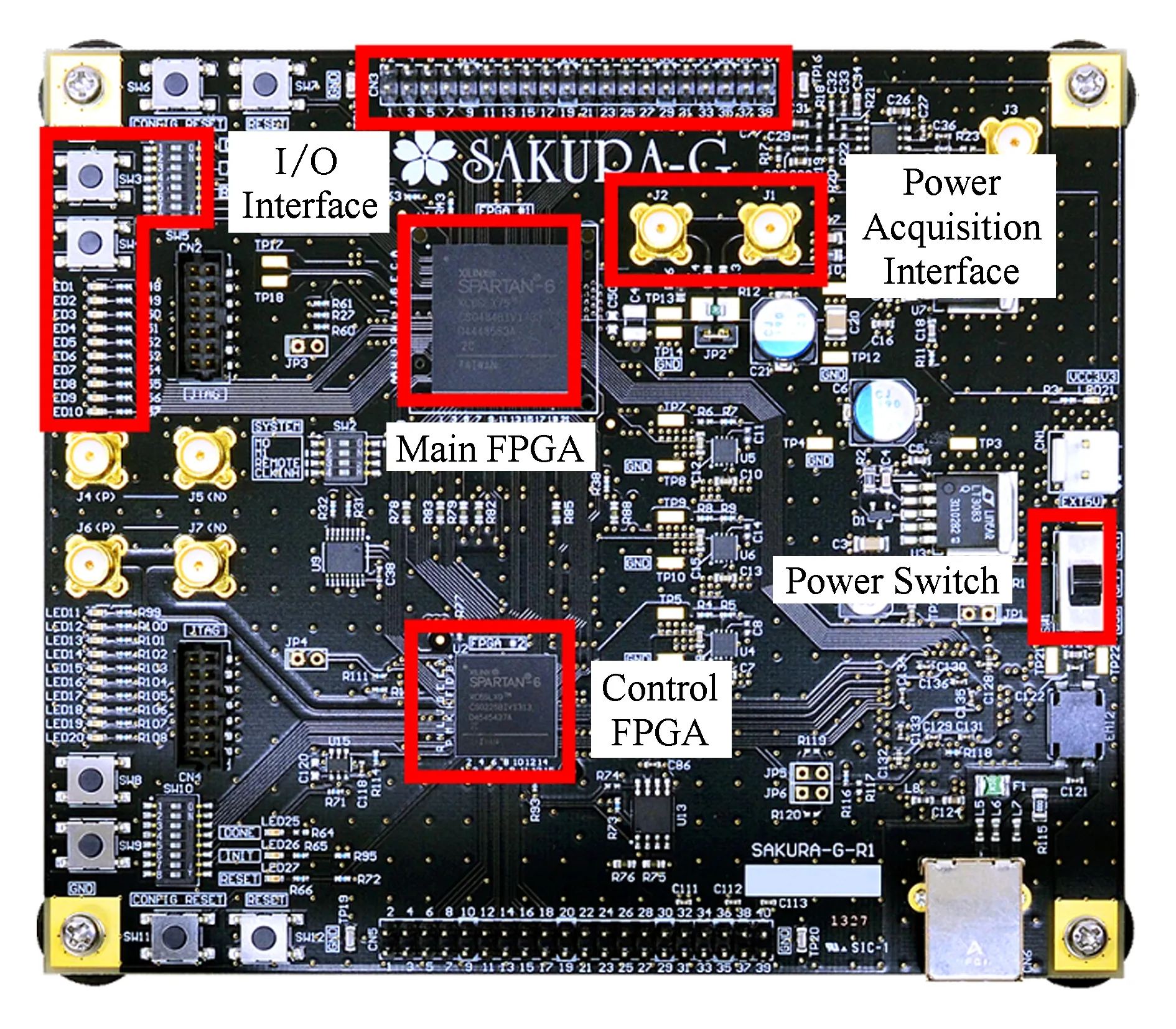
Fig. 3　SAKURA-G FPGA development board.图3　SAKURA-G FPGA开发板

功耗采集平台如图4所示.硬件电路通过Modelsim功能验证后，PC机将SM2运算电路下载至主FPGA，将控制电路下载至控制FPGA，外部向开发板提供3.3V电源.触发控制电路工作，控制电路传送地址、数据和控制等信号给主FPGA中的SM2IP核，示波器通过功耗采集接口采集SM2运行过程的功耗波形，如图5所示.

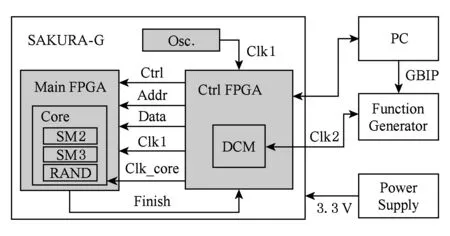
Fig. 4　Architecture of power acquisition platform.图4　功耗采集平台结构示意图

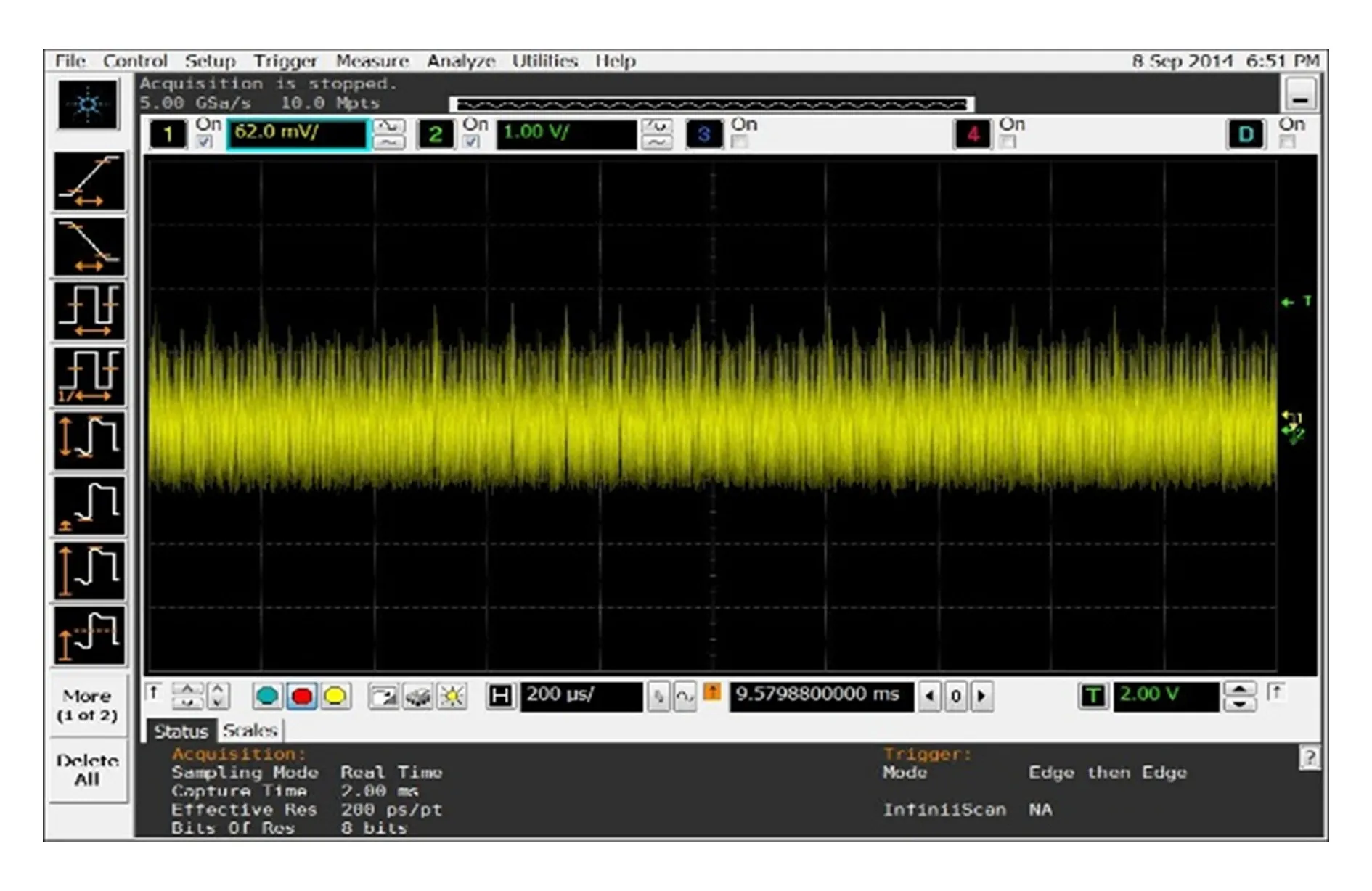
Fig. 5　Power wave of SM2 intermediate operation process.图5　SM2中间运行过程功耗波形

分别采集传统算法和本文算法对应的功耗曲线，进行攻击.对比结果如图6所示，采用传统算法的功耗波形中点加与倍点呈现明显不同的尖峰，可以准确区分点加与倍点，无法抵抗SPA，而采用本文方案的波形中点加与倍点具有相同运算规律，3个尖峰1组，与理论中MUL-ADD-SUB原子结构相符，成功验证本文方案能够抵抗SPA，达到预期目标.

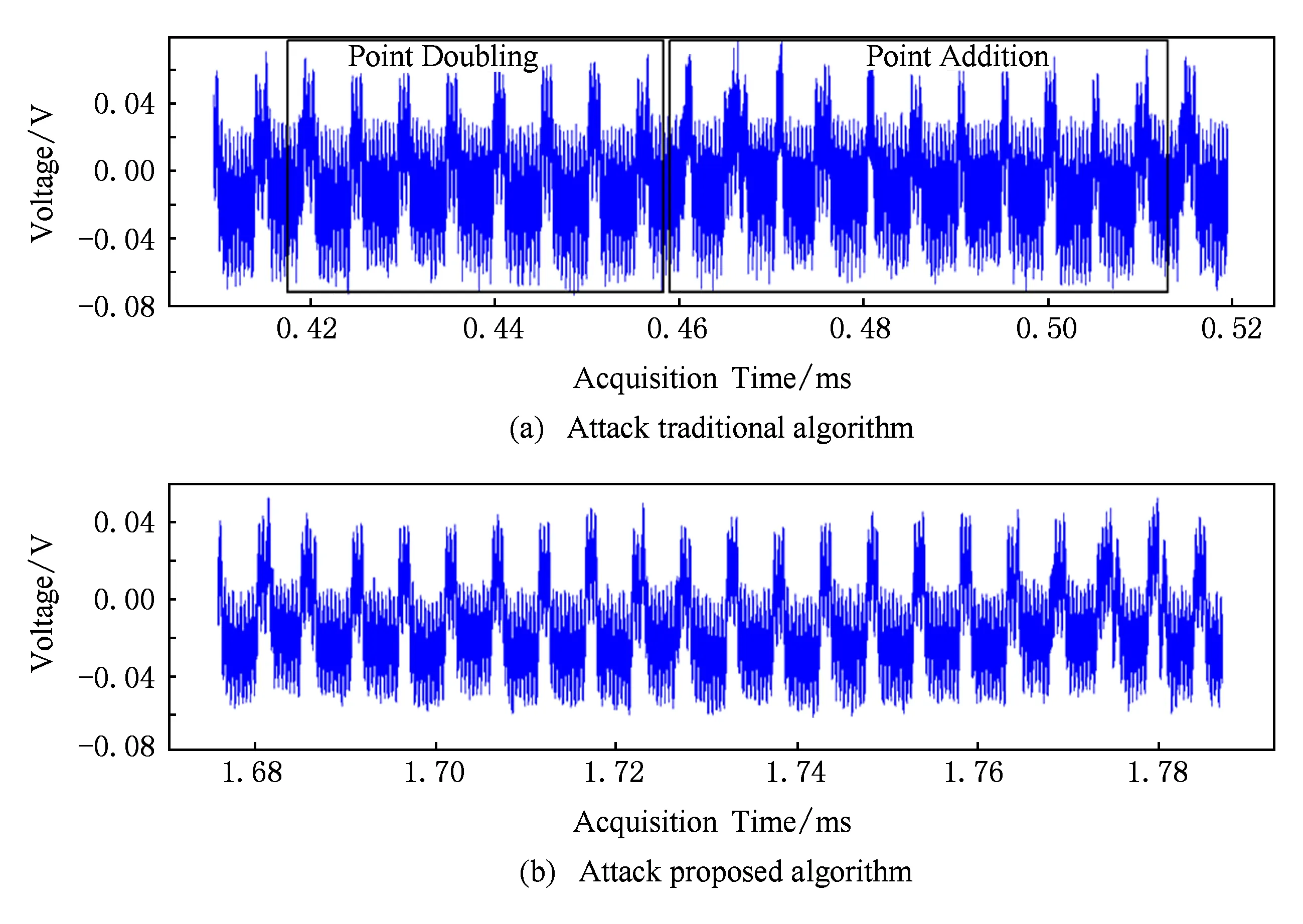
Fig. 6　Comparison of attacks results.图6　攻击结果对比图

3.2运算量分析

传统抗SPA的方法为总执行点加倍点算法，取该算法和前人原子算法与本文方案进行对比，结果如表1所示，其中文献[7，10]与本文均取原型为二进制展开法的改进算法参与对比，点加取固定点加.D，A代表基本点加倍点，D1，A1代表文献[7]中的点加倍点，D2，A2代表文献[10]中的点加倍点，D3，A3代表本文中的点加倍点，M代表模乘，S代表模平方，a代表加减法，R代表求反.D=4M+6S+7a，A=8M+3S+9a.表2为多种原子结构对比，经统计知，D1=4M+6S+20a+10R，A1=8M+3S+22a+11R，D2=4M+4S+24a+16R，A2=8M+3S+33a+22R，D3=4M+4S+16a，A3=8M+3S+22a.令S≈0.8M，a≈0.1M，R≈0.1M.

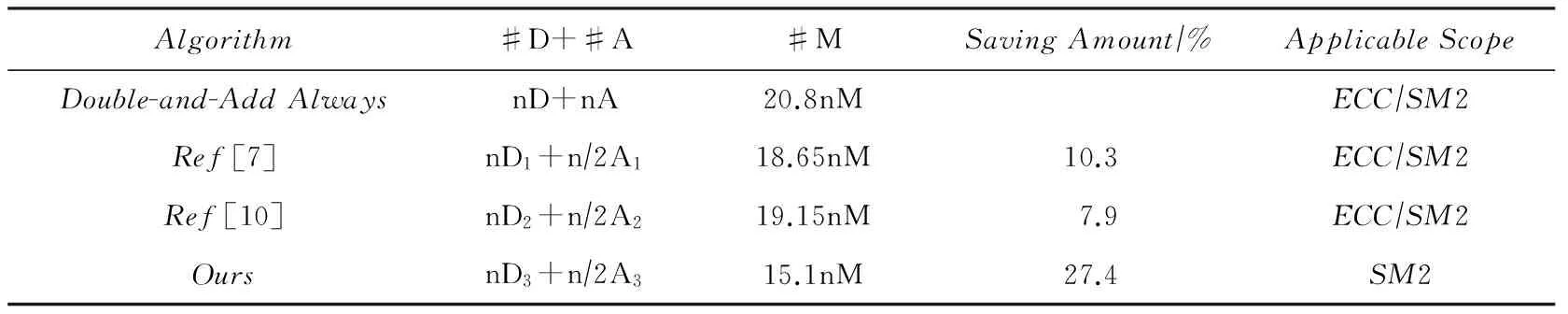
Table 1　Comparison of Cost and Applicable Scope表1　 运算量及适用范围对比

Table 2　Comparison of Different Atomic Structures表2　不同原子结构对比

总执行点加倍点的算法添加了一倍点加操作，计算效率较低，文献[7，10]中方案因原子结构较长，为了构成原子块添加的冗余操作也远大于本文方案.由于文中优化基于SM2标准参数曲线，本文方案仅适用于SM2算法.由表2容易看出，本文算法运算量得到显著降低，比传统算法节约了27.4%，比文献[7]中算法多节约了17.1%，比文献[10]则多节约了19.5%.

4　结束语

本文将原子概念与SM2算法相结合，提出一种新型MUL-ADD-SUB结构的改进原子算法，对其安全性和性能进行了理论评估.经FPGA实际验证，证明所提方案能够有效抵抗SPA.

[1]Koblitz,N.Ellipticcurvecryptosystems[J].MathematicsofComputation, 1987, 48(177): 203-209

[2]MillerVS.Useofellipticcurvesincryptography[C] //ProcofAdvancesinCryptology-CRYPTO’85.Berlin:Springer, 1986: 417-426

[3]ChineseCryptographyAdministration.GM//T0003—2012.SM2ellipticcurvepublickeycryptographicalgorithms[S].Beijing:NationalCommercialCryptographyManagementOffice, 2010 (inChinese)

(国家密码管理局.GM//T0003—2012.SM2椭圆曲线公钥密码算法[S]. 北京: 国家商用密码管理办公室, 2010)

[4]JoyeM.Ellipticcurvesandside-channelanalysis[J].STJournalofSystemResearch, 2003, 4(1): 17-21

[5]FanJ,GuoX,DeMulderE,etal.State-of-the-artofsecureECCimplementations:Asurveyonknownside-channelattacksandcountermeasures[C] //Procofthe2010IEEEIntSymponHardware-OrientedSecurityandTrust(HOST).Piscataway,NJ:IEEE, 2010: 76-87

[6]WalterCD.SimplepoweranalysisofunifiedcodeforECCdoubleandadd[G] //LNCS3156:CryptographicHardwareandEmbeddedSystems-CHES2004.Berlin:Springer, 2004: 191-204

[7]Chevallier-MamesB,CietM,JoyeM.Low-costsolutionsforpreventingsimpleside-channelanalysis:Side-channelatomicity[J].IEEETransonComputers, 2004, 53(6): 760-768

[8]KocherP,JaffeJ,JunB.Differentialpoweranalysis[C] //ProcofAdvancesinCryptology-CRYPTO’99.Berlin:Springer, 1999: 388-397

[9]MamiyaH,MiyajiA,MorimotoH.EfficientCounter-measuresAgainstRPA,DPA,andSPA[M].Berlin:Springer, 2004

[10]WangHong,ZhuFeng.Ellipticcurvescalarmultiplicationalgorithmsbasedonside-channelatomicconcept[J].JournalofElectronicsTechnology, 2012, 25(4): 16-20 (inChinese)

(王宏, 朱峰. 基于边信道原子的椭圆曲线标量乘算法[J]. 电子科技, 2012, 25(4): 16-20)

[11]QinBaodong,KongFanyu.Secureandfastellipticcurvescalarmultiplicationalgorithmsbasedonside-channelatomicconcept[J].JournalofComputerApplications, 2009, 29(11): 2983-2986 (inChinese)

(秦宝东, 孔凡玉. 基于边带信道原子的安全快速椭圆曲线密码点乘算法[J]. 计算机应用, 2009, 29(11): 2983-2986)

HanXiaowei,bornin1991.MasteroftheInstituteofMicroelectronicsofTsinghuaUniversity.HermainresearchinterestiscoutermeasuresagainstsidechannelanalysisofSM2algorithms.

WuLiji,bornin1965.PhD,associateprofessorandPhDsupervisoroftheInstituteofMicroelectronicsofTsinghuaUniversity.Hismainresearchinterestsincludeintegratedcircuitsystemandcommercialinformationsecurity.

WangBeibei,bornin1983.MasterandengineeroftheInstituteofMicroelectronicsofTsinghuaUniversity.Hermainresearchinterestischipinformationsecurity.

WangAn,bornin1983.AssociateresearcherandpostdoctoralresearcheroftheInstituteofMicroelectronicsofTsinghuaUniversity.Hismainresearchinterestsincludecrypto-graphicengineeringandsidechannelattackanddefensetechnology.

AtomicAlgorithmAgainstSimplePowerAttackofSM2

HanXiaowei,WuLiji,WangBeibei,andWangAn

(Institute of Microelectronics, Tsinghua University, Beijing 100084)

SM2algorithmsarecommercialellipticcurvepublic-keyalgorithms,whicharereleasedbyChineseCryptographyAdministrationandsimilartoECC.Traditionalcryptographicalgorithmsalwayshavesecurityflaws.Attackersoftenattackonsecurityweaknessesofalgorithmsandanalyzethesecret-key,whichposesgreatthreattocryptographicsystemsandpeoples’property.Therearevariouskindsofattacks,suchaspowerattack,faultattackandelectromagneticattack.Amongtheseattacks,powerattackisthemosttraditionalone,whichhasmanyadvantagessuchassmallsecret-keysearchingspaceandhighanalysisefficiency.Usually,powerattackutilizesthepowerleakageduringoperationprocessesofcryptographicalgorithms,acquirespowerwavesandretrievesthesecretkey.InordertoresistpowerattackandenhancethesecurityofSM2algorithms,thisarticlelearnsfromellipticcurvecryptographyalgorithms,appliestheatomicconceptintoSM2andproposesanovelatomicalgorithm.Accordingtotheoreticalcomparisonbetweentheproposedalgorithmandotherformeralgorithms,itshowsthattheproposedalgorithmsaves27.4%ofcomputationincomparisontodouble-and-addalwaysalgorithm.Besides,ithaslesscomputationamountthanotheratomicalgorithms.Furthermore,implementationhasbeenfulfilledonSAKURA-GFPGAboard.Simulationresultsdemonstratethattheproposedalgorithmcanresistsimplepowerattacksuccessfully.

SM2;cryptographicsystem;powerattack;ellipticcurvecryptographicalgorithm;atomicalgorithm

2015-01-19；

2015-12-29

“核高基”国家科技重大专项基金项目(2014ZX01032205，2014ZX01032401-001-Z05)；国家自然科学基金项目(61402252，61402536)；信息保障技术重点实验室开放基金项目(KJ-14-006)；北京理工大学青年教师学术启动计划项目

乌力吉 (lijiwu@mail.tsinghua.edu.cn)

TP309

ThisworkwassupportedbythetheNationalScienceandTechnologyMajorProjectsofHegaoji(2014ZX01032205, 2014ZX01032401-001-Z05),theNationalNaturalScienceFoundationofChina(61402252, 61402536),theFoundationofScienceandTechnologyonInformationAssuranceLaboratory(KJ-14-006),andtheBeijingInstituteofTechnologyResearchFundProgramforYoungScholars.