融合社区结构和兴趣聚类的协同过滤推荐算法

郭弘毅　刘功申　苏　波　孟　魁

(上海交通大学电子信息与电气工程学院　上海　200240)



融合社区结构和兴趣聚类的协同过滤推荐算法

郭弘毅刘功申苏波孟魁

(上海交通大学电子信息与电气工程学院上海200240)

(king-guo@sjtu.edu.cn)

传统的协同过滤推荐算法受限于数据稀疏性问题，导致推荐结果较差.用户的社交关系信息能够体现用户之间的相互影响，将其用于推荐算法能够提高推荐结果的准确度，目前的社交化推荐算法大多只考虑了用户的直接社交关系，没有利用到潜在的用户兴趣偏好信息以及群体聚类信息.针对上述情况，提出一种融合社区结构和兴趣聚类的协同过滤推荐算法.首先通过重叠社区发现算法挖掘用户社交网络中存在的社区结构，同时利用项目所属类别信息，设计模糊聚类算法挖掘用户兴趣偏好层面的聚类信息.然后将2种聚类信息融合到矩阵分解模型的优化分解过程中.在Yelp数据集上进行了新算法与其他算法的对比实验，结果表明，该算法能够有效提高推荐结果的准确度.

重叠社区；兴趣聚类；推荐算法；协同过滤；矩阵分解

近年来，随着信息技术和互联网的飞速发展，人们逐渐从信息匮乏的时代走入了信息过载的时代, 如何从海量数据中筛选出有价值的信息是信息消费者和信息提供者都要面对的挑战.推荐系统作为联系用户和信息的工具由此应运而生，它能够使得信息消费者获取对自己感兴趣的信息，同时使得信息提供者能够有针对性地向目标用户投放信息，实现两者的共赢.目前，推荐系统已经不同程度地运用到了多个互联网领域中[1].

推荐算法是推荐系统的关键部分.其中，协同过滤推荐算法是目前应用最为成功的推荐技术之一[2].其主要思想是利用目标用户的消费记录，基于消费行为或者评分相似的用户具有相似消费偏好的假设，找到与目标用户偏好相似的用户集合，根据用户集合的喜好给目标用户推荐其可能感兴趣的项目.相较于基于内容的推荐算法，尽管协同过滤推荐算法不依赖于项目的特征信息，不受限于内容分析技术的局限，但是受限于数据稀疏性问题[3].互联网规模的急速扩张带来了用户数量和项目数量的急剧增长，用户-项目评分信息稀疏，用户间共同消费的项目很少，直接导致推荐结果的准确度下降.

随着Web2.0的迅速发展，互联网用户能够扮演愈发活跃的角色，除了常规的购买和评分行为，还能够与信赖的或志同道合的用户建立信任关系.用户的消费行为也不再仅仅是其个人的兴趣偏好的体现，而且在一定程度上也受到与其具有社交关系的用户的影响.社交网络分析的研究表明，网络社区中，受到社交因素的影响，有社交关联的用户往往会体现出相似的兴趣爱好和行为特征[4].因此，融入用户社会属性的社交化推荐系统成为近年来推荐系统领域的研究热点.其中传统的社交化推荐算法采用了基于信任的模型，利用了用户间的直接信任关系，然而随着互联网规模的不断扩大，用户间的直接信任关系不可避免地出现数据稀疏性的问题.此外，基于信任模型的社交化推荐算法的基本假设是用户的兴趣偏好与其所信任的用户相似或者受到这些用户的影响[5].然而在现实生活中，用户的兴趣偏好是多方面的，其信任的个体间的兴趣偏好也存在差异，单一的直接社交关系并不能刻画出针对不同领域的项目时用户与好友的兴趣偏好的差异性.

基于上述原因，本文提出一种融合社区结构和兴趣聚类的协同过滤推荐算法.通过重叠社区发现算法挖掘用户的社交网络结构中蕴含的社区信息，避免了使用直接社交关系引起的数据稀疏性问题，量化不同用户在社区中的影响力的差异.此外，考虑到同一社区中用户群体的兴趣偏好的差异，利用项目类别信息，挖掘用户兴趣偏好层面的聚类信息.将2种聚类信息融合到基于矩阵分解的协同过滤算法中，通过对矩阵分解过程中的隐式特征向量进行约束来优化目标函数.

1　相关工作

传统的协同过滤推荐算法分成基于内存的方法和基于模型的方法2类[6].近年来，基于矩阵分解模型的协同过滤推荐算法作为基于模型的方法中的一个分支被广泛应用到了推荐系统中.它能够把高维的用户-项目评分矩阵转化成表示用户和项目隐式特征向量的低维矩阵乘积的形式，实现高维数据的降维，在缓解数据稀疏性造成的推荐结果准确度下降问题方面有非常好的效果.文献[7]首先提出了矩阵分解技术在推荐系统领域的应用，文献[8]提出了概率矩阵分解模型，从条件概率最优的角度进行矩阵的概率优化分解，得到了相同的矩阵分解模型.

在社交化推荐算法中，矩阵分解技术融合了用户的各种社会属性信息，基于用户与所信任的用户群体具有相似的兴趣偏好或者受其影响的假设，通过在矩阵优化分解的过程中添加相关约束得到更优的用户隐式特征向量.文献[9]提出了SoRec模型，它是一种社会谱正则化的变形方法，把矩阵分解技术同样作用在信任矩阵上，用户隐式特征向量同时从用户-项目评分矩阵和信任矩阵的优化分解过程中得到.文献[10]提出了STE模型，把用户-项目评分矩阵中的项看作是用户个人偏好以及用户信任好友喜好的组合，在优化分解过程中将用户对项目的评分和用户的朋友对项目的评分加权平均，使得推荐结果拥有了可解释性.文献[11]提出了SocialMF模型，假设用户的隐式特征向量是由其朋友的隐式特征向量决定的，在优化分解过程中引入了信任传播的概念.这些社交化推荐算法只利用了用户的直接社交关系，当直接社交关系稀疏时会导致推荐结果不理想.文献[12]首次在社交化推荐算法中引入了重叠社区发现算法，关注对目标函数中的正则项的约束.提出了2种模型旨在减小用户与其所在社区其他用户的偏好的差异.文献[13]在SocialMF模型的基础上进行改进，区分了对于不同项目类别，用户对不同好友的信任度的差异.算法直接根据项目类别划分用户的好友，因此可能会进一步加剧数据稀疏性问题.文献[14]考虑到信任多样性的特点.对用户信任关系和用户兴趣进行建模识别出目标用户信任且兴趣接近的用户，改进SocialMF模型.但算法仍可能受限于直接社交关系稀疏问题.

2　融合社区结构和兴趣聚类的推荐算法

本文提出的融合社区结构和兴趣聚类的协同过滤推荐算法的流程如图1所示.1)利用重叠社区发现算法挖掘用户社交网络中存在的社区结构，得到基于网络结构的用户集合；2)利用针对数据特性改进的模糊C均值聚类算法，根据项目类别信息和用户行为记录得到基于兴趣偏好相似度的用户集合，分别量化目标用户对其所属的2类不同用户集合的感兴趣程度；3)将2种用户聚类信息融合到矩阵分解模型的优化分解过程中，通过在目标函数中引入新的正则项试图得到更优的分解结果，最终获得用户对项目的预测评分.

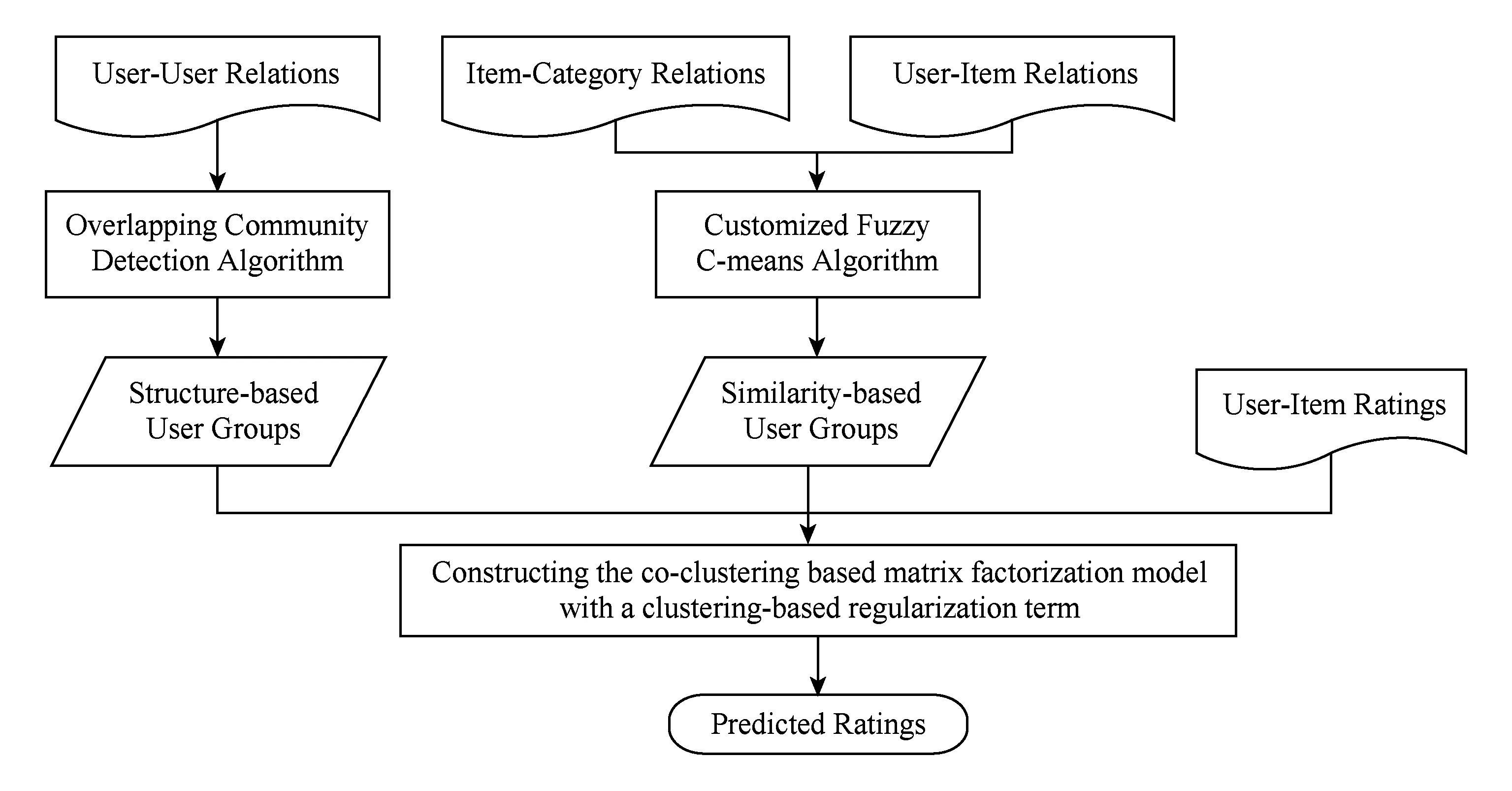
Fig. 1　The flow chart of co-clustering recommendation algorithm.图1　融合双重聚类的推荐算法流程图

2.1准备工作

设U={u1,u2,…,um}表示推荐系统中所有用户的集合，V={v1,v2,…,vn}表示推荐系统中所有项目的集合，C={c1,c2,…,cq}表示推荐系统中所有项目类别的集合，其中m,n,q分别表示用户总数、项目总数、类别总数.R=(Ri j)m×n表示用户-项目评分矩阵，其中Ri j∈{1,2,3,4,5}表示用户ui对项目vj的评分.T=(Ti j)m×m,Ti j∈{0,1}表示用户的社交关系矩阵，Ti j=1表示用户ui与用户uj之间存在好友关系.本文采取双向确认的用户的社交关系，因此矩阵T为对称矩阵.

2.2基于社区结构的聚类

推荐系统中的用户集合以及用户间的社交关系构成了庞大的社交网络，用户往往与其直接好友具有相似的兴趣偏好或者受其影响，一些研究[9-10,15]即根据这个假设在传统的协同过推荐算法加入用户的社交关系信息进行优化.然而在大型社交网络中普遍存在着长尾效应[16]，即社交关系多的用户占总量的少数，而绝大多数用户只有很少的社交关系.因此，有必要在网络中挖掘其他有价值信息.社交网络中总是存在社区结构，同一个社区内的用户具有某些相同的特性，如地理位置相近、行业领域相同、关注的内容主题相近等.社区内的其他用户或多或少地会对用户的选择产生影响.社交网络中的用户往往同属于多个社区，比如用户与其所在城市相同的用户属于一个社区，与喜爱科幻类电影的用户同属于另外一个社区.这些重叠社区信息体现了用户的不同特性.

对于社交网路中的重叠社区发现的研究是近年来社区发现领域的研究热点，本文直接采用其中效果突出的重叠社区发现算法来划分推荐系统中的用户社交网络.BIGCLAM算法是一种适用于大型网络的重叠社区发现算法[17]，它基于社区间重叠部分中的节点紧密连接的假设，在非负矩阵分解模型的基础上进行改进.文献[12]的实验比对结果表明使用BIGCLAM算法得到的社区信息作为社交化推荐算法的约束条件能够取得较好的推荐结果.因此，本文选择BIGCLAM算法划分用户社交网络中的重叠社区.

显然，用户对于其所在的不同社区的感兴趣程度存在差异，文献[12]中设定某个社区内所有用户对应在用户-评分矩阵内的用户评分向量的平均值作为社区评分向量，计算属于该社区的某用户对应的用户评分向量与该社区评分向量的相似度作为该用户对该社区的感兴趣程度.然而社区中的每个用户对该社区做出的贡献是不同的.相对于处于社区结构边缘的用户，在社区中拥有更多与其有直接社交关系的好友的用户更能够代表这个社区.基于该假设考虑社区中所有用户的评分向量和社区好友数量，从而获取带权重的社区评分向量:

(1)

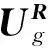
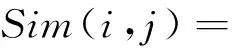
(2)

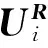
由此，我们得到了基于社交网络结构的用户社区信息，用户评分向量与所属社区的社区评分向量的相似度即表示用户对该社区的感兴趣程度.处在同一社区中的用户具有相同的特性或相互影响.

2.3基于兴趣偏好的聚类

重叠社区发现算法将用户集合根据其社交网络结构进行划分，属于同一社区内的用户存在相同的特性或相互影响.然而同一社区内的用户依然可能存在不同的兴趣偏好.如喜爱科幻电影的用户被划分入一个社区，但他们对于音乐、游戏、饮食的偏好却存在很大差异，因此有必要对同一社交网络社区中的用户进行进一步的划分.基于以上原因，提出了基于兴趣偏好的模糊聚类算法，该算法利用用户的行为记录以及项目所属的类别，寻找与目标用户在泛化层面的兴趣偏好相似的用户集合.

1) 定义用户类别偏好向量

用户评分过的项目可能属于不同的类别，用户对某一类别中的项目的评分数量占的比例与该用户对该类别感兴趣的程度成正比.用户ui评分过的所有项目的所属类别的分布向量可描述如下：

(3)

2) 定义聚类目标函数

模糊C均值聚类(fuzzy C-means)[18]作为模糊聚类分析中的一个比较成熟的算法，在各个领域都有着广泛的应用.其通过优化目标函数来获取每个样本点属于某个类簇的隶属度，即样本点可以同时属于多个类簇，符合推荐系统中用户兴趣偏好的性质.模糊C均值聚类在计算样本点向量和类簇中心点向量的相似度时通常采用的是闵可夫斯基距离.即

(4)

当p=1时，D(X,Y)为曼哈顿距离，当p=2时为欧几里得距离.然而推荐系统中的用户-项目评分矩阵数据稀疏，用户大多只对某几个类别的项目产生过评分行为，导致用户类别偏好向量也存在稀疏性问题，直接使用闵可夫斯基距离公式计算得出的相似度可能会影响聚类的效果.

基于以上原因，需要设计能够处理用户类别偏好向量存在的数据稀疏性问题的相似度测量方式.可描述如下：

(5)

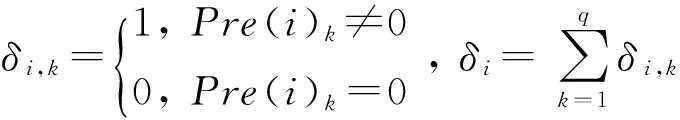
式(5)表示样本点向量与类簇中心向量的相似度.我们假设类簇的数量为l.式(5)中gj表示某个类簇中心点j(j=1,2,…,l)的向量.gj,k为gj中的第k个元素.Dsparse在用户类别偏好向量中选取非零元素即用户产生过评分行为的类别元素计算相似度.

有了相似度表达式，我们接着定义目标函数的表达式:

(6)

3) 聚类算法过程

基于兴趣偏好的模糊聚类算法通过迭代运算，更新用户类簇隶属度矩阵B和类簇中心矩阵G的值，逐步减小目标函数的误差值，当目标函数的误差值收敛至预设阈值时迭代终止.具体过程如下：

② 更新类簇中心矩阵G

(7)

其中，j=1,2,…,l.

③ 更新用户类簇隶属度矩阵B

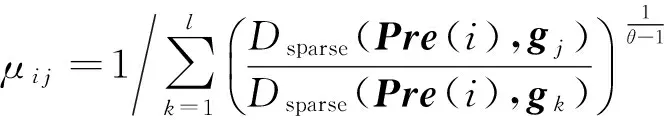
(8)

其中，i=1,2,…,m;j=1,2,…,l.

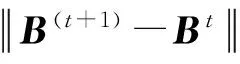
由此，我们得到了基于兴趣偏好的用户模糊聚类，用户类簇隶属度矩阵B中的元素μi j即表示用户ui对兴趣类簇Ψj的感兴趣程度.处在同一类簇中的用户具有相似的泛化兴趣偏好.

2.4融合双重聚类的矩阵分解方法

1) 矩阵分解模型

矩阵分解模型是在协同过滤推荐算法中应用最为广泛的模型之一.其主要思想是将用户-项目评分矩阵R近似地分解成2个低维矩阵乘积的形式：

(9)

(10)

其中,Ii j为指示函数，用户ui对项目vj产生过评分，则Ii j=1，否则Ii j=0.由于用户-项目评分矩阵的稀疏程度很大，在矩阵分解过程中容易出现过拟合问题，因此需要在目标函数中添加合适的正则项.

(11)

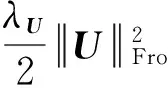
2) 融合双重聚类的矩阵分解模型

在现实生活中，我们所做的决定往往受到好友或者领域权威人士的影响.在2.2节、2.3节中我们得到了用户社交网络社区聚类信息和用户泛化兴趣偏好聚类信息，其中前者将相互影响并且特性相同的用户聚类在一起，后者将多领域兴趣偏好相似的用户聚类在一起.显然目标用户与同一集合中的用户的相似度要高于与之不共享任一集合的用户的相似度，用户的兴趣偏好和与其同在一个集合中的所有用户的平均兴趣偏好接近，并且用户对不同集合的感兴趣程度不同.基于以上假设，我们在文献[20]中提出的矩阵分解模型基础上进行改进，引入新的正则项:

(12)

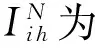
由此，我们提出了一种新的融合双重聚类的矩阵分解模型，记为CCMF(co-clustring based matrix factorization).目标函数如式(13)所示.

(13)

通过随机梯度下降方法得到用户隐式特征矩阵U和项目隐式特征矩阵V的局部最优解.相应的偏导数如式(14) (15)所示.

(14)

(15)

通过不断迭代，沿梯度下降方向更新U和V中的元素直至收敛来训练模型.

3　实验与评估

3.1数据集

本文使用Yelp数据集对算法进行测试.Yelp.com是全球最大的本地商家点评网站之一，它不但允许用户对商家进行点评或者评分，还是一个社交特征明显的互联网公司，鼓励用户之间积极互动，其平台上的用户能与其他用户建立双向确认的好友关系.我们在本文中使用的Yelp数据集是Qian等人在文献[21]中使用的数据集.数据集由8 351位用户、84 653个项目、263 777条项目评分信息以及524 120条用户双向好友关系信息组成.其中，项目评分为[1,5]之间的整数，所有项目总共分为8个类别.表1中是对 Yelp数据集中分类别信息的统计数据.

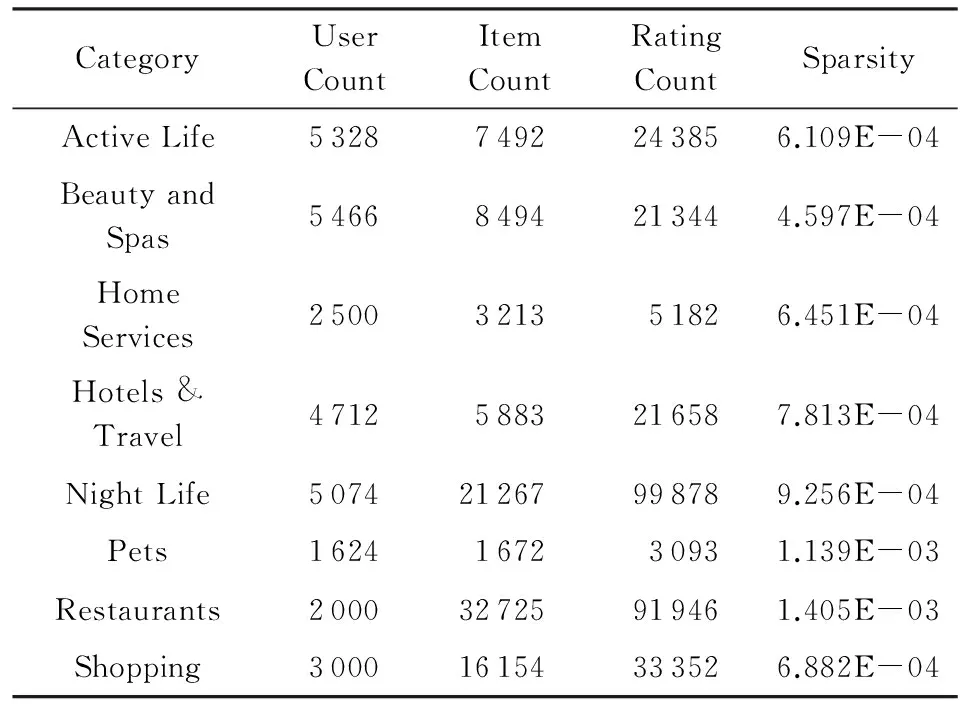
Table 1　Statistic of Per Category表1　数据集分类别统计量

3.2对比算法

为了验证本文提出的算法与其他算法在推荐结果准确度上的差别，我们选择5种算法作为对比算法进行实验.

BaseMF：文献[6]提出的适用于推荐系统的矩阵分解基本模型，没有加入用户的社交关系信息或项目类别信息.

SocialMF：文献>[11]提出的融入用户信任关系信息的矩阵分解模型，假设用户向量是由其好友的用户向量决定的，在优化分解过程中引入了信任传播的概念.

SoReg：文献[20]首次提出了在矩阵分解模型中加入社交化正则项的概念，通过加入社交化正则项使得用户的偏好与其好友偏好的平均值相似.

MFC：文献[12]在矩阵分解模型中引入了重叠社区发现算法，在SoReg算法的基础上区分了用户所在社区不同的差异.

CircleCon：文献[13] 依据针对不同的项目类别，用户对其好友的信任关系存在差异的假设，在SocialMF算法的基础上根据项目类别划分了用户信任网络.

3.3评价指标

本文使用五重交叉验证作为实验方法.将数据集随机分为5份，每次选择其中的4份即数据集的80%作为训练集，选择余下的一份即数据集的20%作为测试集，将5次的评估结果取平均值得到最终的评估数据.

由于本文提出的协同过滤算法的目标是为了提高推荐结果的准确度，因此我们采用平均绝对误差(mean absolute error,MAE)和均方根绝对误差(root mean square error,RMSE)作为实验的评估方法.

(16)

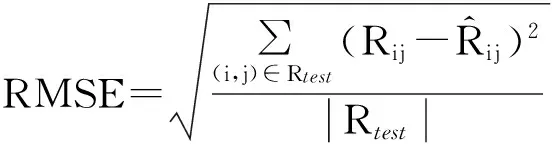
(17)

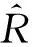
3.4实验结果及分析

1) 确定兴趣类簇l的值

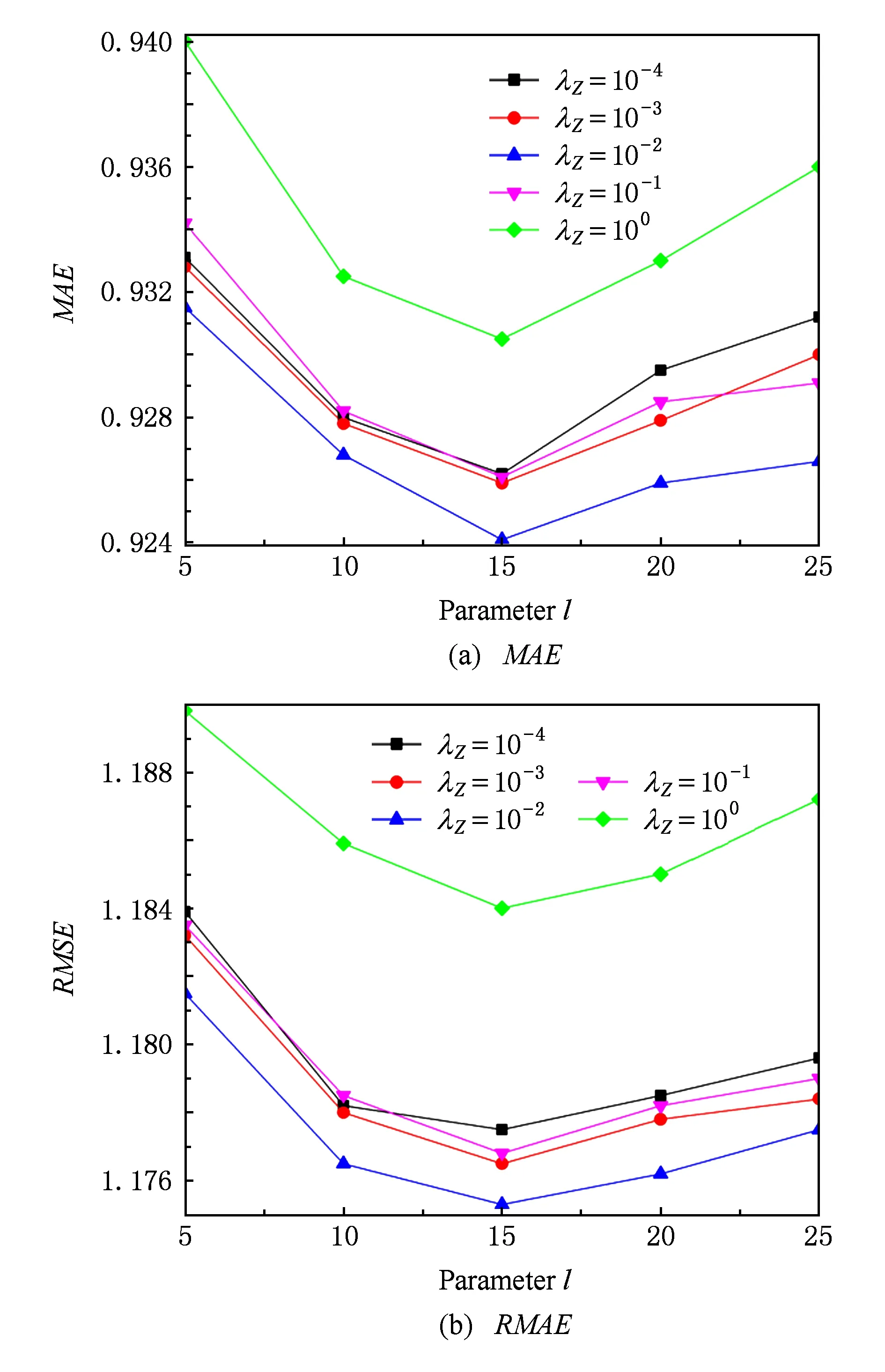
Fig. 2　Impact of parameter l.图2　兴趣类簇l的值对准确度的影响

兴趣类簇l的值代表了根据所有用户的行为记录以及项目的类别信息划分的泛化兴趣类簇数量.在实验中我们选择将l的值从5～25以步长5增加，记录推荐结果的MAE值和RMSE值随不同l值的变化情况.为了更加清楚地了解l值对推荐结果产生的影响，我们根据正则项系数λZ值的不同，分5组进行实验.实验结果如图2所示：

从图2中可以看到，对于不同的λZ值，推荐结果的准确度随不同l值的变化情况基本相同，使用l值过大或者过小都会对推荐结果产生负面的影响.当l=15时，推荐结果的MAE值和RMSE值同时达到最小.分析其可能原因，如果兴趣类簇的数量设定得过小，经过模糊聚类划分出的类簇结果并不能清晰地划分用户在不同兴趣爱好的层面的分布情况；而兴趣类簇的数量设定得过大时，经过模糊聚类划分出的类簇过多，可能削弱了其对用户泛化兴趣爱好的表达.

2) 确定正则项系数λZ的值

Fig. 3　Impact of parameter λZ.图3　正则项系数λZ的值对准确度的影响

正则项系数λZ表示用户社交网络重叠社区信息以及兴趣偏好模糊聚类信息在矩阵分解模型中参与的比重，当λZ=0时本文提出的模型即相当于基本的矩阵分解模型.将λZ的值分别取值为{0.0001,0.001,0.01,0.1,1}进行实验.记录推荐结果的MAE值和RMSE值随不同λZ值的变化情况.同样地，为了更加清楚地了解λZ值对推荐结果产生的影响，我们根据不同的兴趣类簇l的值，分5组进行实验.如图3所示：

从图3中可以看到，对于不同的l值，推荐结果的准确度随不同λZ值的变化情况基本相同.当λZ取值较小时，推荐结果的MAE值和RMSE值相对较高，随着λZ取更大的值，MAE值和RMSE值减小，当λZ=0.01时同时达到最优的准确度.而继续增加λZ的值后，准确度再次降低.分析其可能原因，当λZ取值过小时，算法引入的附加信息对结果造成的影响微弱，不足以体现其在获得更优的用户隐式特征向量中所做的贡献；而λZ取值过大时，附加信息在优化向量过程中的权重过大造成过度影响.

3) 不同推荐算法的推荐效果对比

通过之前实验的对比和分析，可知当兴趣类簇l=15，正则项系数λZ=0.01时，本文提出的CCMF算法能够获得最优的推荐结果.为了进一步验证CCMF算法的有效性，我们将CCMF算法与3.2节中介绍的相关算法进行了对比实验.首先通过五重交叉验证确定实验中所有算法的参数.常规正则项系数λU和λV均取值为0.01，用户和项目的隐式特征向量维数均取10.在SocialMF，SoReg，MFC，CircleCon算法中，社交正则项系数λZ分别设为0.01,0.01,0.001,0.01.SoReg中的β值设为0.5.实验结果如表2所示：

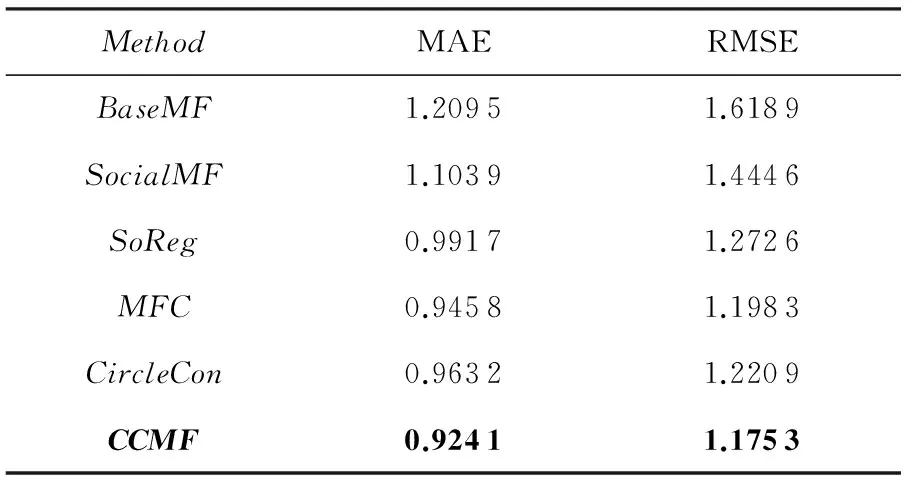
Table 2　Comparison of CCMF and Other Methods表2　CCMF算法与其他算法的实验结果对比

从表2中可以看到，本文提出的融合社区结构和兴趣聚类的协同过滤算法相较于其他算法，推荐结果的准确度更高.分析其可能的原因，BaseMF算法由于没有考虑任何用户-项目评分矩阵以外的信息所以推荐效果最差.SocialMF，SoReg，MFC算法没有同时利用用户社交信息和项目类别信息.CircleCon算法直接将用户根据其评分过的项目所属类别进行划分，然而单个项目类别下的用户的社交关系可能存在数据稀疏问题.本文提出的CCMF算法一方面使用用户重叠社区信息，一定程度上缓解了用户的社交关系的稀疏性问题；另一方面，针对泛化兴趣偏好的模糊聚类为用户隐式特征向量提供了更有利的约束条件.因此能够得到更好的推荐效果.

4　结束语

基于直接社交关系的传统社交化推荐算法面临用户社交信息稀疏的问题，而且没有考虑用户兴趣偏好对社交关系造成的影响，导致推荐结果不理想.为了解决这一缺陷，本文提出了一种在矩阵分解模型中融合社区结构和兴趣聚类的协同过滤推荐算法.利用重叠社区发现算法挖掘用户的社交关系层面的聚类，同时根据项目类别信息设计算法实现对用户兴趣偏好的模糊聚类，并且能够量化用户对不同社区或类簇的感兴趣程度.通过实验证明该算法比现有算法能够得到更优的推荐结果.

[1]KantorPB,RokachL,RicciF,etal.RecommenderSystemsHandbook[M].Berlin:Springer, 2011: 1-2

[2]SuX,KhoshgoftaarTM.Asurveyofcollaborativefilteringtechniques[J//OL].AdvancesinArtificialIntelligence, 2009[2016-02-25].http://dl.acm.org//citation.cfm?id=1722966

[3]AdomaviciusG,TuzhilinA.Towardthenextgenerationofrecommendersystems:Asurveyofthestate-of-the-artandpossibleextensions[J].IEEETransonKnowledgeandDataEngineering, 2005, 17(6): 734-749

[4]KrebsV.Socialnetworkanalysis:Anintroduction[J//OL]. 2015 [2016-02-25].http://www.orgnet.com//sna.html

[5]YangX,GuoY,LiuY,etal.Asurveyofcollaborativefilteringbasedsocialrecommendersystems[J].ComputerCommunications, 2014, 41: 1-10

[6]BobadillaJ,OrtegaF,HernandoA,etal.Recommendersystemssurvey[J].Knowledge-BasedSystems, 2013, 46: 109-132

[7]KorenY,BellR,VolinskyC.Matrixfactorizationtechniquesforrecommendersystems[J].Computer, 2009, 42(8): 30-37

[8]SalakhutdinovR,MnihA.Probabilisticmatrixfactorization[C] //Procofthe20thNeuralInformationProcessingSystems(NIPS’07).Cambridge:MITPress, 2007

[9]MaH,YangH,LyuMR,etal.Sorec:Socialrecommendationusingprobabilisticmatrixfactorization[C] //Procofthe17thACMConfonInformationandKnowledgeManagement(CIKM’08).NewYork:ACM, 2008: 931-940

[10]MaH,KingI,LyuMR.Learningtorecommendwithsocialtrustensemble[C] //Procofthe32ndIntACMSIGIRConfonResearchandDevelopmentinInformationRetrieval(SIGIR’09).NewYork:ACM, 2009: 203-210

[11]JamaliM,EsterM.Amatrixfactorizationtechniquewithtrustpropagationforrecommendationinsocialnetworks[C] //Procofthe4thACMConfonRecommenderSystems(RecSys’10).NewYork:ACM, 2010: 135-142

[12]LiH,WuD,TangW,etal.Overlappingcommunityregularizationforratingpredictioninsocialrecommendersystems[C] //Procofthe9thACMConfonRecommenderSystems(RecSys’15).NewYork:ACM, 2015: 27-34

[13]YangX,SteckH,LiuY.Circle-basedrecommendationinonlinesocialnetworks[C]//Procofthe18thACMSIGKDDIntConfonKnowledgeDiscoveryandDataMining(KDD’14).NewYork:ACM, 2012: 1267-1275

[14]GuoLei,MaJun,ChenZhumin.Truststrengthawaresocialrecommendationmethod[J].JournalofComputerResearchandDevelopment, 2013, 50(9): 1805-1813 (inChinese)

(郭磊, 马军, 陈竹敏. 一种信任关系强度敏感的社会化推荐算法[J]. 计算机研究与发展, 2013, 50(9): 1805-1813)

[15]MassaP,AvesaniP.Trust-awarecollaborativefilteringforrecommendersystems[C] //ProcofonOntheMovetoMeaningfulInternetSystemsConfederatedIntConf.Berlin:Springer, 2004: 492-508

[16]FortunatoS.Communitydetectioningraphs[J].PhysicsReports, 2010, 486(3): 75-174

[17]YangJ,LeskovecJ.Overlappingcommunitydetectionatscale:Anonnegativematrixfactorizationapproach[C] //Procofthe6thACMIntConfonWebsearchandDataMining(WSDM’13).NewYork:ACM, 2013: 587-596

[18]BezdekJC,EhrlichR,FullW.FCM:Thefuzzyc-meansclusteringalgorithm[J].Computers&Geosciences, 1984, 10(2): 191-203

[19]XuR,WunschD.Surveyofclusteringalgorithms[J].IEEETransonNeuralNetworks, 2005, 16(3): 645-678

[20]MaH,ZhouD,LiuC,etal.Recommendersystemswithsocialregularization[C] //Procofthe4thACMIntConfonWebSearchandDataMining(WSDM’11).NewYork:ACM, 2011: 287-296

[21]QianX,FengH,ZhaoG,etal.Personalizedrecommendationcombininguserinterestandsocialcircle[J].IEEETransonKnowledgeandDataEngineering, 2014, 26(7): 1763-1777

GuoHongyi,bornin1992.Master.Hismainresearchinterestsincluderecommendersystemanddatamining(king-guo@sjtu.edu.cn).

LiuGongshen,bornin1974,PhD,associateprofessorandmastersupervisor.MemberofChinaComputerFederation,Hisresearchinterestsincludeinformationsecurityanddatamining(lgshen@sjtu.edu.cn).

SuBo,bornin1972.Associateprofessorandmastersupervisor.Hisresearchinterestsincludeimageprocessingandmachinelearning(subo@sjtu.edu.cn).

MengKui,bornin1973.PhD.Herresearchinterestsincludeinformationsecurityandprivacyprotection(mengkui@sjtu.edu.cn).

Collaborative Filtering Recommendation Algorithm Combining Community Structure and Interest Clusters

Guo Hongyi, Liu Gongshen, Su Bo, and Meng Kui

(ShoolofElectronicInformationandElectricalEngineering,ShanghaiJiaoTongUniversity,Shanghai200240)

Traditional collaborative filtering recommendation algorithms suffer from data sparsity, which results in poor recommendation accuracy. Social connections among users can reflect their interactions, which can be mixed into recommendation algorithms to improve the accuracy. Only straightforward social connections have been used by most current social recommendation algorithms, while users’ latent interest and cluster information haven’t been considered. In response to these circumstances, this paper proposes a collaborative filtering recommendation algorithm combining community structure and interest clusters. Firstly, overlapping community detection algorithm is used to detect the community structure existed in user social network, thus users in the same community have certain common characteristics. Meanwhile, we design a customized fuzzy clustering algorithm to discover users’ interest clusters, which uses item-category relationship and users’ activity history as input. Users in the same cluster are similar in generalized interest. We quantify users’ preference for each social community and interest cluster they belong to respectively. Then, we combine this two types of user group information into matrix factorization model by adding a clustering-based regularization term to improve the objective function. Experiments conducted on the Yelp dataset show that, in comparison to other methods including both traditional and social recommendation algorithms, our approach gets better recommendation results in accuracy.

overlapping community; interest cluster; recommendation algorithm; collaborative filtering; matrix factorization

2016-03-17；

2015-05-24

国家“九七三”重点基础研究发展计划基金项目(2013CB329603)；国家自然科学基金项目(61472248, 61431008)

TP311; TP181

This work was supported by the National Basic Research Program of China (973 Program) (2013CB329603) and the National Natural Science Foundation of China (61472248,61431008).