基于Ranking的泊松矩阵分解兴趣点推荐算法

余永红　高　阳　王　皓

(计算机软件新技术国家重点实验室(南京大学)　南京　210023) (江苏省软件新技术与产业化协同创新中心　南京　210023)



基于Ranking的泊松矩阵分解兴趣点推荐算法

余永红高阳王皓

(计算机软件新技术国家重点实验室(南京大学)南京210023) (江苏省软件新技术与产业化协同创新中心南京210023)

(yuyh.nju@gmail.com)

随着基于位置社交网络(location-based social network, LBSN)的发展，兴趣点推荐成为满足用户个性化需求、减轻信息过载问题的重要手段.然而，已有的兴趣点推荐算法存在如下的问题：1)多数已有的兴趣点推荐算法简化用户签到频率数据，仅使用二进制值来表示用户是否访问一个兴趣点；2)基于矩阵分解的兴趣点推荐算法把签到频率数据和传统推荐系统中的评分数据等同看待，使用高斯分布模型建模用户的签到行为；3)忽视用户签到数据的隐式反馈属性.为解决以上问题，提出一个基于Ranking的泊松矩阵分解兴趣点推荐算法.首先，根据LBSN中用户的签到行为特点，利用泊松分布模型替代高斯分布模型建模用户在兴趣点上签到行为；然后采用BPR(Bayesian personalized ranking)标准优化泊松矩阵分解的损失函数，拟合用户在兴趣点对上的偏序关系；最后，利用包含地域影响力的正则化因子约束泊松矩阵分解的过程.在真实数据集上的实验结果表明：基于Ranking的泊松矩阵分解兴趣点推荐算法的性能优于传统的兴趣点推荐算法.

基于位置社交网络；兴趣点推荐；泊松矩阵分解；BPR标准；地域影响力

近年来，基于位置社交网络(location-based social network, LBSN)应用迅速增长，受到工业界和学术界的广泛关注.典型的基于位置的社交网络应用包括Foursquare*https://foursquare.com//, Gowalla*http://gowalla.com//, GeoLife*http://research.microsoft.com//en-us//projects//geolife//, Facebook Place*https://www.facebook.com//places//等.在这些基于位置的社交网络服务应用中，用户可以与其他用户建立社交联系，探索周边的环境，以签到兴趣点(如餐馆、购物中心和景点等)的方式分享生活经历.LBSN除了为用户提供交互平台，其中包含的丰富数据(签到数据、社交关系、评论信息等)可以用来挖掘用户的兴趣偏好，并为用户推荐用户可能感兴趣的、未访问过的地理位置.为用户推荐用户可能感兴趣的地理位置的任务称为兴趣点(point-of-interest, POI)推荐.兴趣点推荐一方面满足了用户的个性化需求，减轻用户面临的信息过载问题，另一方面，兴趣点推荐帮助LBSN服务提供商实现智能化的位置服务，如位置感知的广告服务等，从而增加LBSN服务提供商的营业收入.因此，兴趣点推荐在基于位置的社交网络中扮演越来越重要的角色.

虽然推荐系统[1]已经被学术界深入研究，并在电子商务系统中得到广泛应用，如Amazon*http://www.amazon.com//中的商品推荐，Netflix*https://www.netflix.com//中的电影推荐，Last.fm*http://www.last.fm//中的音乐推荐和淘宝*https://www.taobao.com//中的商品推荐等，但是，LBSN中兴趣点推荐系统近年才逐渐流行.不同于传统的推荐系统，兴趣点推荐系统具有如下独特属性：

1) 隐式反馈频率数据.在传统的推荐系统中，用户一般使用显式评分表达用户的偏好.用户的评分通常在一定的范围内，如[1,5].用户评分越高表示用户越满意.不同于传统的推荐系统，在LBSN中，用户的偏好是由用户的隐式签到数据表示.相对于评分数据，签到频率的范围较大.例如，用户可能在一些兴趣点上签到几百次，而在某些兴趣点上仅签到几次.另外，兴趣点推荐系统中仅包含正例，而传统的推荐系统中可能同时包含正例和负例.因此，兴趣点推荐可以看作OCCF(one-class collaborative filtering)问题[2-3].

2) 地域影响.在LBSN中，用户与兴趣点之间存在物理的交互，这是兴趣点推荐系统有别于传统推荐系统的一个显著特点.由于用户签到活动涉及到用户与兴趣点之间的物理交互，从访问成本的角度而言，用户往往访问距离近的兴趣点.另外，Tobler的第一地理学法则[4]表明：相对于距离远的兴趣点，距离近的兴趣点之间更加相似.

3) 社交影响力.基于朋友之间往往具有共同偏好的假设，文献[5-8]利用用户之间的社交网络关系来改进传统推荐算法的性能.然而，对于兴趣点推荐而言，前面的研究工作[9]表明大约96%的用户仅共享少于10%的访问偏好，意味着大量的朋友在兴趣点方面没有共同偏好.因此，社交影响力在兴趣点推荐系统中对用户的签到行为影响有限.

基于上述兴趣点推荐系统的独特属性，现有的兴趣点推荐算法利用上述属性来扩展传统的推荐算法，以支持LBSN中的兴趣点推荐任务.例如，Ye等人[10]提出了一种变异的User-based协同过滤[11]兴趣点推荐算法，此兴趣点推荐算法在User-based 协同过滤框架中集成了用户偏好、地域影响力和社交影响力.Cheng等人[12]在矩阵分解模型中融合地域影响和社交影响,从而为用户提供兴趣点推荐.Zhang等人[13]利用用户与兴趣点之间的地域影响、社交影响和类别相关性，提出了GeoSoca兴趣点推荐算法.不同于文献[10,12-13]从用户的角度建模地域影响，Liu等人[14]从兴趣点的角度利用地域影响力，并提出了IRenMF兴趣点推荐算法.最近，Lian等人[15]利用权重矩阵分解模型进行兴趣点推荐，并在权重矩阵分解模型中集成了地域影响力.

虽然近年来研究人员提出了一些兴趣点推荐算法，但是已有的兴趣点推荐算法存在如下的问题：

1) 多数已有的兴趣点推荐算法简化用户签到频率数据，即不管用户在一个兴趣点上签到多少次，使用二进制值来表示用户是否访问一个兴趣点.换句话说，用户-兴趣点签到频率矩阵简化为01矩阵.直观地，用户的签到频率反映了用户对兴趣点的偏好程度.在一个兴趣点上的签到次数越多，用户可能更加偏好此兴趣点.因此，简化用户的签到频率数据不能准确地捕获用户对兴趣点的偏好.

2) 基于矩阵分解的兴趣点推荐算法把签到频率数据和传统推荐系统中的评分数据等同看待，使用高斯分布模型建模用户的签到行为.实际上，高斯分布适合建模用户的评分行为，但是不适合建模用户的签到行为.我们随机从MovieLens100K和Foursquare数据集中抽取一个用户，他们各自评分和签到频率分布如图1所示.由图1可以观察: ①高斯分布可以很好地拟合MovieLens100K中的用户评分数据，但是在拟合Foursquare签到频率数据方面，效果并不理想.②相对于高斯分布，泊松分布拟合签到频率数据好于高斯分布.

3) 传统的推荐系统中一般利用样本正例和负例来学习推荐模型，而兴趣点推荐系统中用户反馈信息是隐式的，即仅观测到样本正例，负例和缺失项混合在一起.因此，利用传统的推荐模型很难为用户提供准确的兴趣点推荐.

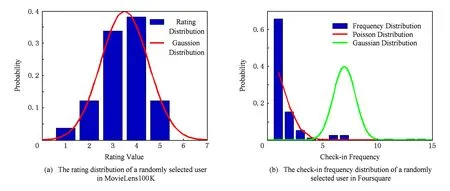
Fig. 1　The rating and check-in frequency distribution in MovieLens100K and Foursquare.图1　MovieLens100K和Foursquare中随机选择用户的评分与签到频率分布

为了解决以上的问题，本文提出了基于Ranking的泊松矩阵分解兴趣点推荐算法.首先，为了更加准确地捕获用户对兴趣点的偏好，使用泊松分布来建模用户的签到行为;其次，为解决兴趣点推荐中的隐式反馈问题，利用BPR(Bayesian personalized ranking, BPR)[16]标准来优化泊松矩阵分解的损失函数;最后，为了进一步改进推荐算法的性能，利用包含地域影响力的正则化因子约束泊松矩阵分解的过程.在真实数据集上的实验结果表明，本文提出基于Ranking的泊松矩阵分解兴趣点推荐算法的性能优于传统的兴趣点推荐算法.

1　相关研究工作

本节主要介绍2类典型的兴趣点推荐算法，包括基于内存的兴趣点推荐算法和基于模型的兴趣点推荐算法.

将兴趣点看作传统推荐系统中的项目(电影、音乐和商品等)，传统推荐系统中基于内存和基于模型的推荐算法可以用在LBSN中为用户提供兴趣点推荐服务.基于内存的协同过滤算法使用整个用户-项目评分矩阵进行推荐，它的基本假设为：与当前活动用户(active user)爱好相似的用户喜欢的项目，当前活动用户可能也喜欢；或者，与用户以前喜欢过的项目相似的项目，用户也可能喜欢.协同过滤的方法首先通过某种相似度度量指标找到当前活动用户或者目标项目的相似用户或者相似项目，然后取相似用户对目标项目的评分平均权重或当前活动用户对相似项目的评分平均权重作为当前活动用户对目标项目的预测评分.User-based协同过滤[11]和Item-based协同过滤[17]是经典的基于内存的推荐算法，Ye 等人[10]利用用户在兴趣点的签到记录计算用户之间的相似度，提出了基于User-based的兴趣点推荐算法.另外，他们在User-based协同过滤框架中融合了社交和地域影响力.Ye等人[10]的实验结果表明User-based的兴趣点推荐算法优于Item-based的兴趣点推荐算法.Levandoski等人[18]将旅行距离作为惩罚因子，提出了基于Item-based的兴趣点推荐算法.Yuan等人[19]考虑用户访问兴趣点的时间因素，在User-based框架上提出了Time-aware兴趣点推荐算法.

自Netflix竞赛以来，由于在处理大规模用户数据方面良好的可扩展性和准确的预测能力，基于矩阵分解的推荐算法[20]受到学术界和工业界的广泛关注.基于矩阵分解的推荐算法认为仅少量的隐藏因子影响用户的偏好和刻画项目的特征.因此，基于矩阵分解的推荐算法将用户和项目的特征向量同时映射到低维的隐藏因子空间.在低维的隐藏因子空间中，由于用户偏好和项目特征之间的相关性可以直接计算，矩阵分解的推荐算法利用用户和项目的低维特征向量的内积来预测用户对项目的评分.在兴趣点推荐方面，矩阵分解模型也得到广泛的应用.例如，Cheng等人[12]提出了基于概率矩阵分解(pro-babilistic matrix factorization, PMF)[21]和社交正则化因子的兴趣点推荐算法，其次，作者在矩阵分解和社交影响力的基础上，进一步集成地域影响力，以改善兴趣点推荐算法性能.不同于文献[9-10,12]从用户的角度建模地域影响，Liu等人[14]从兴趣点的角度利用地域影响力，假定距离近的兴趣点或者属于相同区域的兴趣点共享类似的用户偏好，并提出了IRenMF兴趣点推荐算法.Liu等人[22]提出了地理概率因子分析框架GTBNMF.GTBNMF在贝叶斯非负矩阵分解基础上集成了地域信息和评论文本信息.Gao等人[23]在经典矩阵分解模型基础上，融合评论信息、社交网络信息和地理信息提供兴趣点推荐服务.最近，Lian等人[15]提出了GeoMF兴趣点推荐模型，将用户签到信息看作隐式反馈，在权重矩阵分解模型的基础上集成了地域影响力.此方法通过对已观测项赋值较高权重，缺失项赋值低权重的方法拟合用户的签到数据.

上述基于矩阵分解模型的兴趣点推荐算法简化用户在兴趣点上的签到频率数据，或者将用户签到频率数据与传统推荐系统的评分信息完全等同看待，使用高斯分布建模用户的签到行为.根据引言部分的介绍可知，简化或者使用高斯分布模型不能准确的捕获用户对兴趣点的偏好.不同于上述介绍的基于矩阵的兴趣点推荐算法，本文提出的基于Ranking的泊松矩阵分解兴趣点推荐算法使用泊松分布来建模用户的签到行为，并利用BPR标准来优化泊松矩阵分解的损失函数，更加准确建模用户隐式反馈信息.

2　兴趣点推荐问题描述及泊松矩阵分解

2.1兴趣点推荐问题的形式化描述

在典型的LBSN中，兴趣点推荐系统通常包含2种实体集合：M个用户集合U={u1,u2,…,uM}和N个地点集合L={l1,l2,…,lN}.用户u访问过的兴趣点集合表示为Lu.每个兴趣点除唯一标识外，由〈经度，纬度〉进行地理编码.用户的签到记录组成用户-兴趣点签到频率矩阵F∈M×N, 签到频率矩阵F中每个元素fi j表示用户i在兴趣点j上的签到频率.用户签到的频次反映了用户对兴趣点的偏好程度.通常情况下，用户仅仅访问一小部分的兴趣点，因此，用户-兴趣点签到频率矩阵F极度稀疏.如本文实验部分使用的Foursquare 数据集99.18%的数据缺失.兴趣点推荐的目的是利用用户的签到数据和LBSN中的其他信息预测用户对未签到兴趣点的访问频次i j，并根据预测频次为用户提供可能感兴趣的兴趣点列表.

2.2泊松矩阵分解

泊松因子模型(Poisson factor model, PFM)[24]是一种产生式的概率模型,其概率图模型如图2所示:

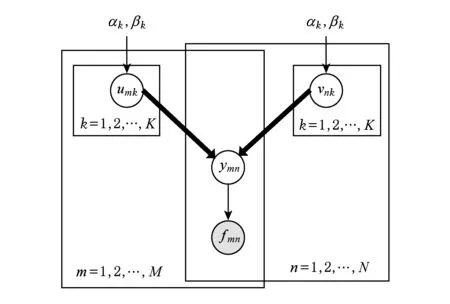
Fig. 2　The probabilistic graphical model for PFM.图2　PFM的概率图模型

PFM假设每个观测元素fm n服从期望为ym n的泊松分布：fm n～Poisson(ym n).期望值矩阵Y∈M×N被分解为用户隐藏特征矩阵U∈M×K和项目隐藏特征矩阵V∈N×K，其中K≪min(M,N)是隐藏特征向量的维数，并使用用户隐藏特征矩阵U和项目隐藏特征矩阵V的内积来近似期望值矩阵Y：Y～UVT.另外，PFM假设隐藏特征矩阵中的每个元素um k和vn k服从Gamma先验分布：

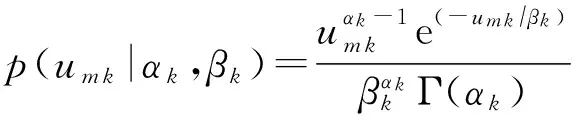
(1)

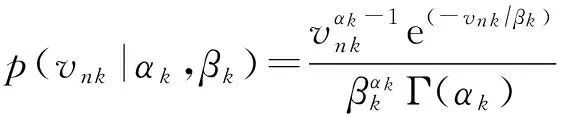
(2)

其中,Γ(·)为伽玛函数，参数αk和βk为Gamma分布的形状参数和尺度参数.因此，用户隐藏特征矩阵U和项目隐藏特征矩阵V的先验分布为

(3)

(4)

其中α=(α1,α2,…,αK)，β=(β1,β2,…,βK).

F中的每个观测值fm n的产生过程如下：

1) 根据Gamma分布为用户隐藏特征向量中的每个元素赋值，um k～Gamma(αk,βk),∀k.

2) 根据Gamma分布为项目隐藏特征向量中的每个元素赋值，vn k～Gamma(αk,βk),∀k.

3) 计算用户m与项目n交互频次的期望值ym n,

4) 根据泊松分布以及期望值ym n生成观测值fm n,

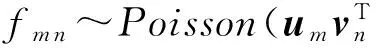
因此，给定Y,F的Poisson概率分布为

(5)

给定用户观测值矩阵F和隐藏特征矩阵的先验，用户隐藏特征矩阵U和项目隐藏特征矩阵V的后验分布为

p(U,V|F,α,β)∝p(F|Y)p(U|α,β)p(V|α,β).

(6)

最大化对数后验概率得到如下的目标函数：

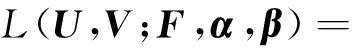
(7)

PFM通过随机梯度下降算法(stochastic grad-ient descent, SGD)来学习用户隐藏特征矩阵U和项目隐藏特征矩阵V.

3　基于Ranking的泊松矩阵分解的兴趣点推荐算法

本节详细描述本文提出的基于Ranking的泊松矩阵分解的兴趣点推荐算法.

泊松因子模型和传统的矩阵分解推荐算法一般将缺失值看作样本负例，直接拟合用户-兴趣点签到频率矩阵中的非缺失项.这种方法不能有效地从非观测项中区分出实际的样本负例和缺失项，而且忽略了来自兴趣点签到频率成对比较之间的偏序关系.

本文采用BPR标准，根据用户在兴趣点上的签到频率值，构建用户-兴趣点偏好训练集，拟合用户对兴趣点的偏好关系，而不是拟合用户对兴趣点的签到频率，优化BPR标准来学习用户隐藏特征矩阵和兴趣点隐藏特征矩阵.

具体地，我们假设：用户访问兴趣点的频次越高，用户偏好此兴趣点的程度越高；用户对访问过兴趣点的偏好程度高于未访问兴趣点.设fm i和fm j分别表示用户m在兴趣点i和j上的签到频次，如果fm i>fm j，那么针对用户m，兴趣点i的偏好排名高于兴趣点j，即li≻mlj，其中≻m表示用户对于所有兴趣点的偏序关系.如果用户在2个兴趣点上都没有签到信息，则无法推导它们之间的偏序关系.形式化地，用户-兴趣点偏好训练集为

DF{(m,i,j)|i,j∈L,m∈U}.

(8)

三元组(m,i,j)表示用户m对兴趣点i的偏好程度高于兴趣点j.

给定用户m，为了找到用户m对所有兴趣点的偏序关系≻m，使用最大后验概率p(Θ|≻m)的方法学习隐藏特征矩阵U和V.根据贝叶斯推理，有：

p(Θ|≻m)∝p(≻m|Θ)p(Θ),

(9)

其中，Θ表示模型参数，即Θ=(U,V).

假定每个用户对兴趣点的访问是独立的，并且针对具体用户，兴趣点对(i,j)上偏序关系独立于其他兴趣点对偏序关系.所有用户在全部兴趣点上的偏序关系的似然函数为

(10)

其中I(x)为指示函数，如果x为真，则I(x)取值为1，否则取值为0.由于用户偏序关系的整体属性和非对称属性，式(10)简化为

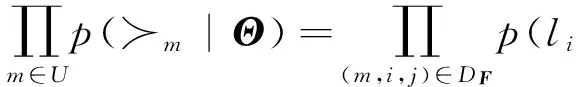
(11)

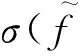
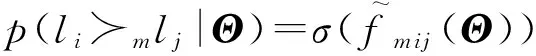
(12)其中,σ(x)为logistic函数σ(x)=1表示用户m在兴趣点i与兴趣点j上的预测访问频次差.

另外，与泊松矩阵分解模型类似，假设隐藏特征矩阵U和V中的每个元素um k和vn k服从Gamma先验分布：

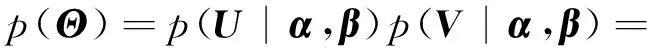
(13)

(14)

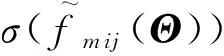
(15)

另外，Tobler的第一地理学法则[4]表明：任何事物都是相关的，但是，相对于距离远的事物，距离近的事物之间更加相关.而且，不同于传统的推荐系统，LBSN中用户签到活动涉及到用户与兴趣点之间的物理交互，为了节约访问成本，用户往往访问距离近的兴趣点.为了进一步改善兴趣点推荐算法的性能，本文通过地域正则化因子来约束泊松矩阵分解过程，即在学习兴趣点隐藏特征矩阵V的过程中，考虑地域影响力因素.地域正则化因子定义为

(16)

其中,λg为正则化控制参数.Sim(n,g)表示兴趣点n与兴趣点g之间的相似度.N(ln)表示与兴趣点n相似的兴趣点集合.我们使用高斯函数来定义兴趣点n与兴趣点g之间的相似度Sim(n,g)：

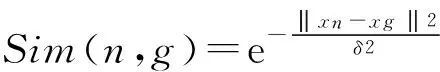
(17)其中，xn和xg表示兴趣点n与兴趣点g的地理坐标向量.δ为常数，本文实验中设置为0.1.在式(17)中，2个兴趣点的距离越近，则相似度越大，反之越小.

在由式(16)定义的地域正则化因子中，兴趣点n的隐藏特征向量vn依赖于相似兴趣点的隐藏特征向量.因此，如果2个兴趣点距离越近，相似度越大，它们共享较为相似的用户签到偏好，则2个兴趣点隐藏特征向量的距离越小.对于一些具有较少签到数据的兴趣点而言，虽然无法准确从与之相关的签到数据中学习到它们的隐藏特征向量，但是与它们相似的兴趣点可能具有足够的签到数据.这些相似的兴趣点的隐藏特征向量可以从签到数据中推导，因此从一定程度上保证了泊松矩阵分解中可以推导出具有较少签到数据兴趣点的隐藏特征向量.

在式(15)中加上地理正则化项后，本文提出的基于Ranking的泊松矩阵兴趣点推荐算法的目标公式为

(18)

由于用户兴趣点偏好关系数量(|F||L|)非常庞大,在所有偏序关系上更新隐藏特征向量运算开销巨大.类似于BPR[16], 我们采用随机梯度下降的算法学习隐藏向量.对于随机采样偏序关系(m,i,j)，目标函数L*关于um k，vi k和vj k的梯度为

(19)

(20)

(21)

其中N(lw)为与兴趣点w相似兴趣点集合.

4　实验与分析

为了验证本文提出的基于Ranking的泊松矩阵分解兴趣点推荐算法的性能，本文在真实的数据集与其他经典的兴趣点推荐算法进行了对比分析.

4.1数据集介绍

本文选择2个公开数据集*http://www.ntu.edu.sg//home//gaocong//datacode.htm：Foursquare和Gowalla，验证本文提出推荐算法的性能.在Four-square数据集中，所有的签到数据是在Singapore收集的，时间范围从2010-08—2011-07.在Gowalla数据集中，所有签到数据是在California 和Nevada收集的，时间范围从 2009-02—2010-10.在2个数据集中，少于5条签到记录的用户和兴趣点被清除.Foursquare数据集包含194 108条签到记录，用户数量为2 321，兴趣点数量为5596.Gowalla数据集包含456 967条签到记录，用户数量为10 162，兴趣点数量为24 237.根据用户和兴趣点的唯一标识，聚合用户的签到记录，我们分别从Foursquare和Gowalla数据集中得到包含105764和307591条观测记录的用户-兴趣点签到频率矩阵.Foursquare和Gowalla数据集的稀疏度分别为99.18%和99.88%.因此，2个数据集都非常稀疏.在Foursquare中，用户平均签到45.57个兴趣点；在Gowalla中，用户平均签到30.27个兴趣点.不同签到频率下，用户的数量分布如图3所示.从图3可以观察到，2个数据集基本符合Power-Law分布.Foursquare和Gowalla数据集的统计信息如表1所示.

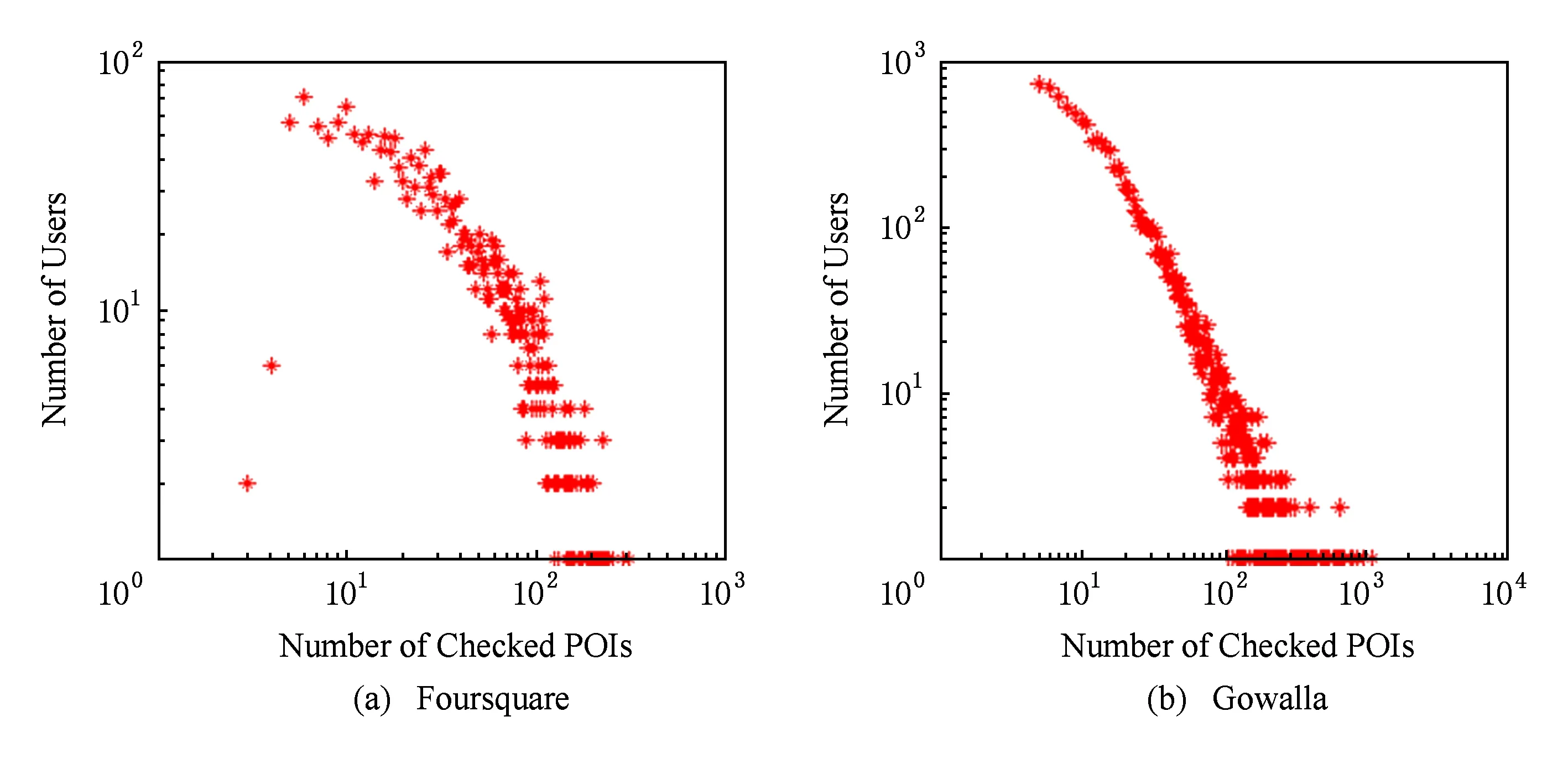
Fig. 3　The distribution of the number of users.图3　用户数量的分布

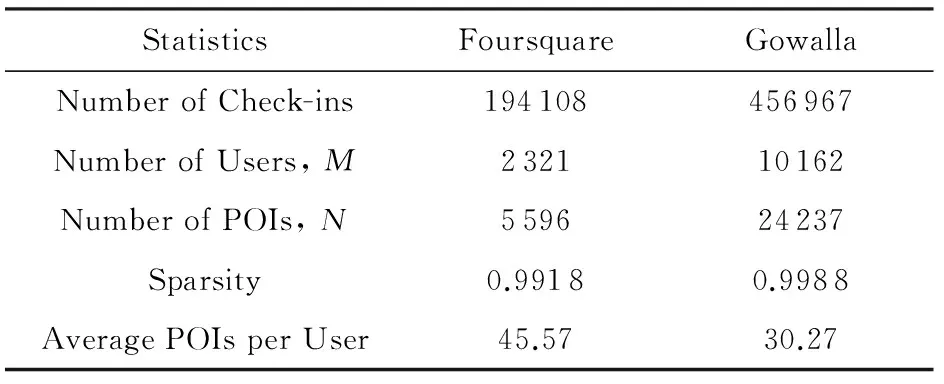
Table 1　Statistics of Foursquare and Gowalla表1　数据集统计信息

4.2度量指标

由于兴趣点推荐系统为每个用户提供基于Ranking的兴趣点推荐列表，本文采用2个被广泛使用的Rank指标评估兴趣点推荐算法性能，即precision@k和recall@k,其中k为推荐列表的长度.给定用户u，兴趣点推荐准确率precisionu@k和召回率recallu@k的定义为

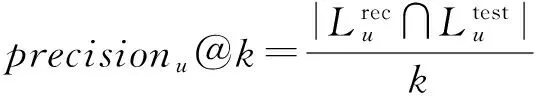
(22)

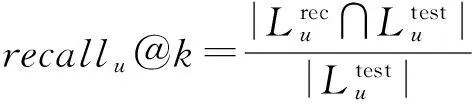
(23)

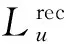
4.3实验设置

为了验证本文提出兴趣点推荐算法的有效性，我们选取如下的典型兴趣点推荐算法作为对比方法：

1) UserKNN.UserKNN是User-based协同过滤推荐算法[11]在兴趣点推荐上的应用.在UserKNN中，基于用户的签到频率数据，采用Cosine相似度指标计算用户之间的相似度.

2) ItemKNN.ItemKNN是Item-based协同过滤推荐算法[17]在兴趣点推荐上的应用.在Item-KNN中，基于用户的签到频率数据，采用Cosine相似度指标计算兴趣点之间的相似度.

3) PMF.PMF由Mnih 和Salakhutdinov[21]提出.PMF通过带高斯噪音的概率图模型来表示隐藏特征向量.PMF是一种经典的矩阵分解算法,可以看作是 SVD模型的概率扩展.

4) WRMF.WRMF是一种权重矩阵分解推荐算法[2-3].WRMF通过给样本正例和样本负例赋值不同的权重，采用逐点的方式来应对推荐系统中的OCCF问题.

5) BPR-MF.BPR-MF采用BPR[16]标准来Ranking项目.BPR-MF采用逐对的方式处理推荐系统中的OCCF问题.在本文实验中，采用均匀采样的策略采样用户-兴趣点对训练模型.

6) PFM.PFM由Ma等人[24]提出.PFM最初用在网站推荐领域，通过泊松分布拟合用户访问网站的频率数据.

7) GeoMF.GeoMF是由Lian等人[15]提出的一种兴趣点推荐算法.GeoMF在WRMF基础上，通过扩展用户和兴趣点隐藏特征向量的方式，融合了空间聚类属性来进行兴趣点推荐.

对于每个用户，我们随机从用户-兴趣点签到频率矩阵中抽取80%的数据作为训练数据，剩余20%数据作为测试数据.为了公平对比，我们参照对比算法的相应文献或者实验结果设置不同算法的参数，在这些参数设置下，各对比算法取得最优性能.在UserKNN和ItemKNN中，用户或者兴趣点相似邻居数量为30；在PMF中，λU=λV=0.001；在WRMF中，λ=0.001，α=1；在BPR-MF中，λΘ=1；在PFM中，αk=20，βk=0.2,k=1,2,…,K；在GeoMF中，γ=0.01，α=10；对于本文提出的方法，αk=20，βk=0.2,k=1,2,…,K，Foursquare上λg=0.1,Gowalla上λg=0.3.我们设置PMF的学习比率η=0.03，其他基于矩阵分解兴趣点推荐算法的学习比率η=0.001.

需要注意的是：经典的兴趣点推荐算法简化用户的签到数据，即利用01来表示用户是否访问过兴趣点.因此，UserKNN和ItemKNN利用用户-兴趣点01矩阵来计算用户或者兴趣点之间的相似度；PMF，WRMF，GeoMF在用户-兴趣点01矩阵上学习用户和兴趣点的隐藏特征向量；BPR-MF在用户-兴趣点01矩阵上构建用户-兴趣点偏好训练集；PFM和本文提出兴趣点推荐算法直接分解用户-兴趣点签到频率矩阵，学习用户和兴趣点隐藏特征向量.

4.4性能对比

在隐藏特征向量维度值开K=10情况下，所有对比算法在2个数据集上的实验结果如表2和表3所示.

从表2和表3可以发现：

1) 在2个数据集上，除PMF外，UserKNN和ItemKNN的性能比基于矩阵分解模型的兴趣点推荐算法性能差，说明基于矩阵分解模型的兴趣点推荐算法一般优于基于内存的兴趣点推荐算法.

2) 在基于内存的兴趣点推荐算法中，UserKNN的推荐准确性高于ItemKNN.这是由于大量兴趣点

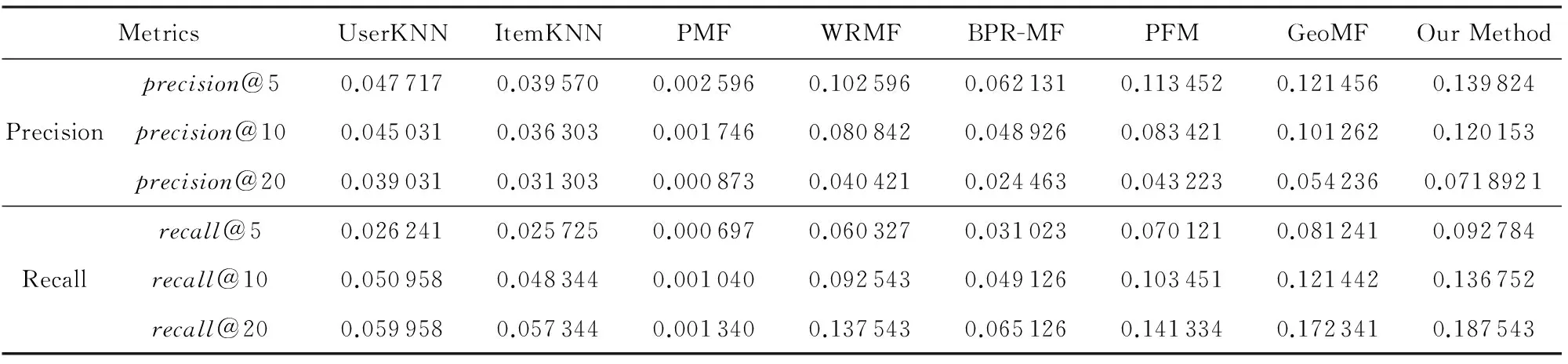
Table 2　Performance Comparison on Foursquare表2　在Foursquare数据集上的性能对比

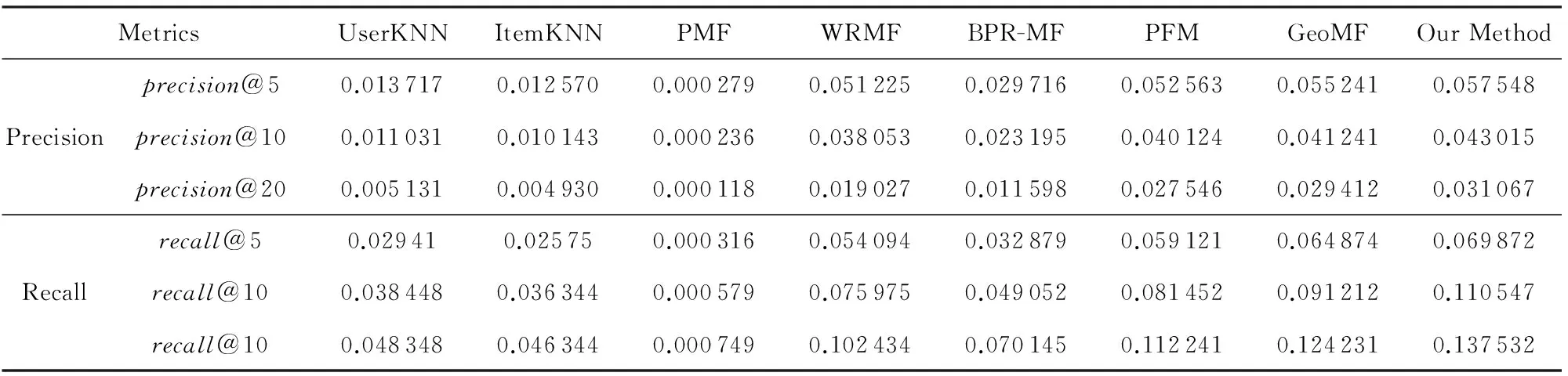
Table 3　Performance Comparison on Gowalla表3　在Gowalla数据集上的性能对比

共享较少的用户签到数据，导致兴趣点之间的相似度不如用户之间相似度计算准确.这个观察结果与文献[10]的观察结果一致.

3) 在所有对比算法中，基于PMF的兴趣点推荐算法的准确率和召回率最低.造成PMF推荐性能差的原因是：PMF假设用户的签到数据服从高斯分布，而实际上，高斯分布模型不适合建模用户签到频率数据.

4) 尽管BPR-MF，WRMF，GeoMF都将兴趣点推荐问题看作OCCF推荐问题，但是BPR-MF性能表现不如WRMF和GeoMF.一种可能的解释是BPR-MF潜在地假设用户在兴趣点上的签到行为服从高斯分布.

5) PFM模型的推荐性能优于PMF，BPR-MF，WRMF,表明泊松分布模型比高斯分布模型更适合建模用户在兴趣点上的签到行为.这个观察结果也表明了PFM模型在兴趣点推荐任务上的潜力.

6) 在2个数据集上，本文提出的基于Ranking泊松矩阵分解兴趣点推荐算法的性能优于其他对比算法，验证了本文提出算法的有效性.与对比算法中的最优结果对比，以precision@5为度量指标，本文提出算法在Foursquare和Gowalla数据集上改进幅度分别为：15.1%，4.2%；以recall@5为度量指标，本文提出算法在Foursquare和Gowalla 数据集上改进幅度分别为：14.2%，7.7%.这个观察结果说明利用泊松分布建模用户的签到行为，以Ranking的方式拟合用户在兴趣点对上的偏序关系，同时通过地域影响正则化因子约束泊松矩阵分解过程，可以有效地提高兴趣点推荐算法性能.

7) 在所有评价指标上，所有对比算法在Foursquare数据集上性能好于它们在Gowalla上的性能.这是由于Foursquare中用户签到兴趣点平均数量高于Gowalla, Gowalla数据集更为的稀疏，而且Foursquare数据集中仅包含1个城市的签到数据，Gowalla数据集中包含2个城市的签到数据.签到数据集的稀疏性和地域的跨度都会影响到兴趣点推荐算法的性能.

4.5参数λg的影响

在本文提出的兴趣点推荐算法中，参数λg是影响兴趣点推荐性能的重要参数.在模型参数学习过程中，参数λg平衡用户的签到信息和兴趣点的地理信息.较大的λg值意味着在学习隐藏特征向量过程中更加依赖兴趣点的地理位置信息.在极端的情况下，如λg=∞，本文提出的兴趣点推荐算法完全依赖于兴趣点的地理位置信息来学习隐藏特征向量，而忽视用户的签到信息.相反，较小的λg值意味着本文提出的兴趣点推荐算法赋予用户的签到信息更多的权重.如λg=0时，本文提出的兴趣点推荐算法完全通过用户的签到信息来学习隐藏特征向量，而忽视相似的兴趣点共享相似用户签到行为的事实.因此，较大或者较小的λg值都将导致本文提出算法性能的下降.在本节中，设置λg为0，0.01，0.1，0.3，0.5，1，5来评估参数λg对本文提出兴趣点推荐算法的影响.其他参数的设置为：αk=20，βk=0.2,k=1,2,…,K,K=10.

实验结果如图4和图5所示.在图4和图5中，我们仅显示precision@5和recall@5在2个数据集上的结果，其他评价指标与precision@5和recall@5呈现类似的变化趋势.从图4和图5可以观察，参数λg对本文提出兴趣点推荐算法的性能具有较大的影响.在2个数据集上，随着参数λg的增大，precision@5和recall@5开始上升，推荐性能提高；λg达到某阈值后，precision@5和recall@5随着λg的增加开始下降，推荐性能降低.另外，在2个数据集上，precision@5和recall@5没有在相同的λg值下达到最优值，说明参数λg的取值随数据集的属性而变化.在Foursquare和Gowalla上，precision@5和recall@5分别在λg=0.1和λg=0.3时取得最佳性能.这可能是由于Gowalla数据集中的签到数据比Foursquare相对稀疏，因此本文提出的兴趣点推荐算法依赖地理信息的权重相对大.

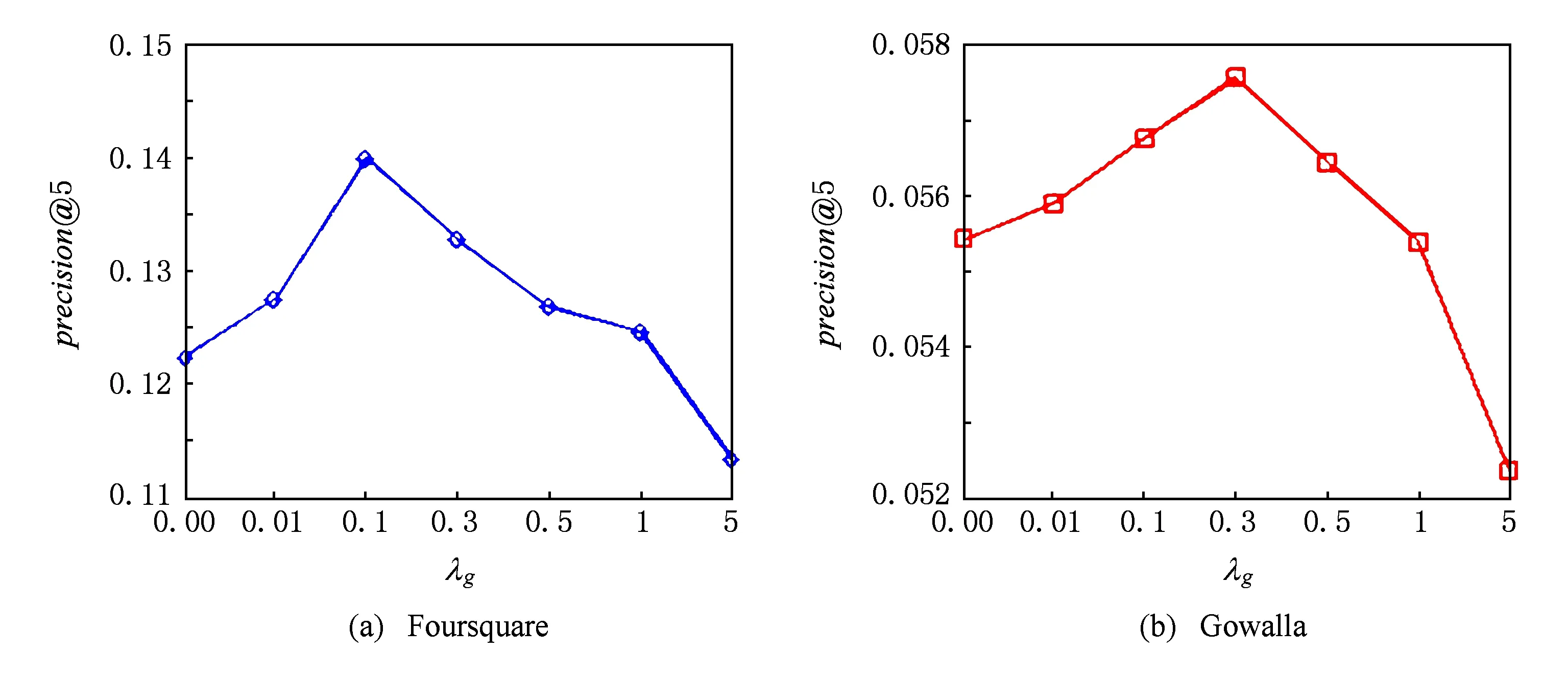
Fig. 4　The impact of λgon precision@5.图4　参数λg对precision@5影响

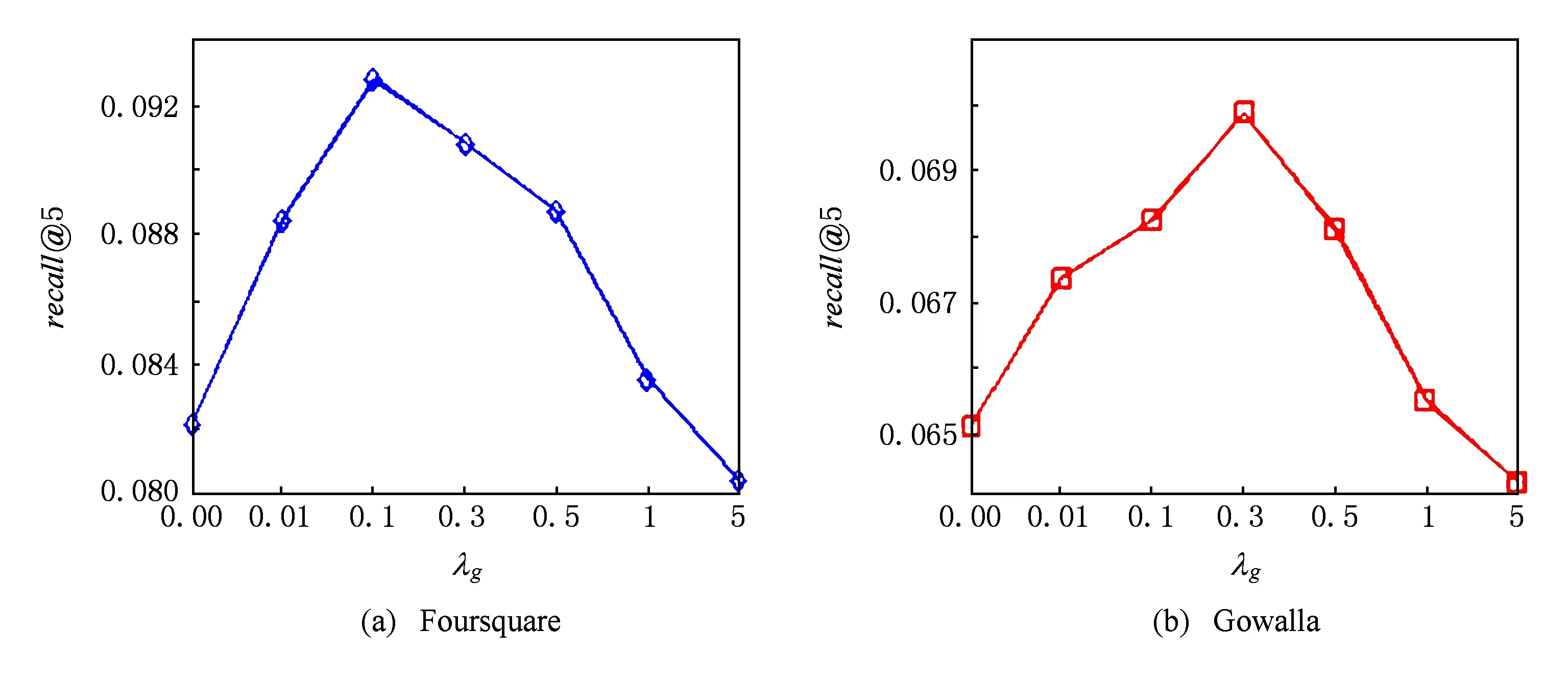
Fig. 5　The impact of λgon recall@5.图5　参数λg对recall@5影响

4.6参数αk和βk的影响

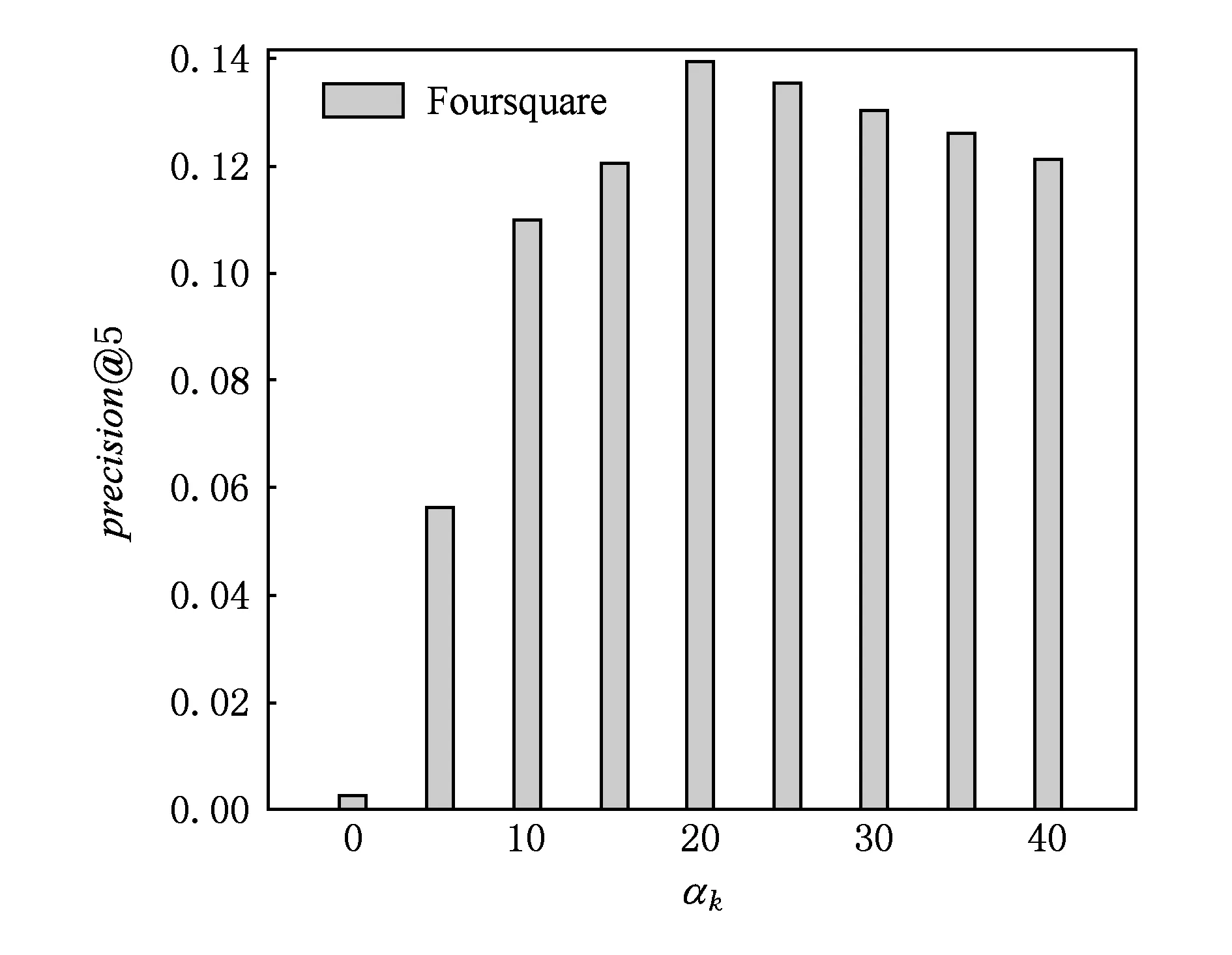
Fig. 6　The impact of αkon precision@5.图6　参数αk对precision@5影响

在本文提出的兴趣点推荐算法中，参数αk和βk是另外2个影响推荐性能的重要参数.参数αk和βk控制Gamma分布的形状和尺度.在本节中，我们固定αk=20，变化βk的值，从0.1～0.5；或者固定βk=0.2，变化αk的值，从0～40，观察precision@5在Foursquare上的变化情况.另外，λg=0.1.

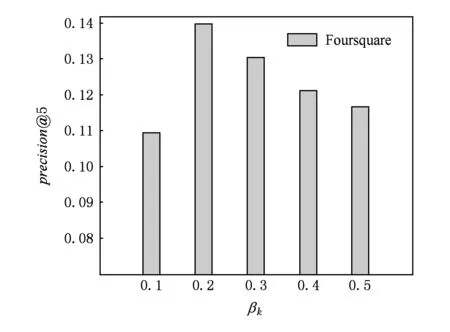
Fig. 7　The impact of βkon precision@5.图7　参数βk对precision@5影响

图6和图7显示了Foursquare数据集上precision@5对参数αk和βk的敏感程度.在Gowalla数据集上，precision@5对参数αk和βk的敏感程度呈现类似的变化趋势.从图6和图7可以看出，参数αk和βk确实对本文提出的兴趣点推荐算法性能具有较大的影响.固定βk，变化αk的值，或者固定αk,变化βk值，precision@5都是先上升，兴趣点推荐准确性提高，到达最优值后，precision@5开始下降，兴趣点推荐准确性降低.这表明较大或者较小的αk和βk都有损本文提出的兴趣点推荐算法性能.

4.7参数K的影响

在本文提出的兴趣点推荐算法中，隐藏特征向量的维数K也是影响兴趣点推荐算法性能的重要参数.我们变化K的值，从5～30，递增步长为5，观察precision@5和recall@5在Foursquare数据集上的变化情况.其他参数设置为：λg=0.1,αk=20,βk=0.2.

实验结果如图8和图9所示.从如图8和图9可以观察：随着K的递增，precision@5和recall@5的值先增加，达到最优值后，precision@5和recall@5

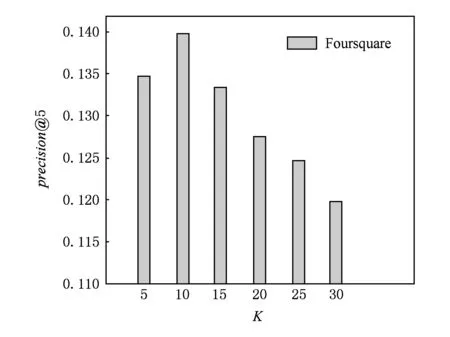
Fig. 8　The impact of K on precision@5.图8　参数K对precision@5影响

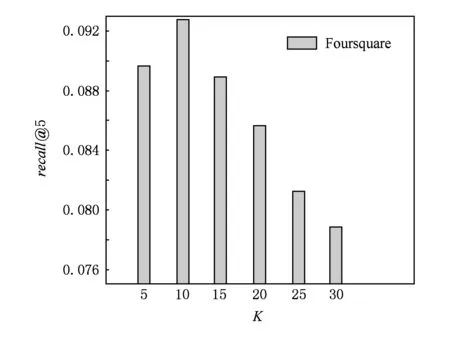
Fig. 9　The impact of K on recall@5.图9　参数K对recall@5影响

随K的递增而降低.在Gowalla数据集上，参数K对precision@5和recall@5的影响呈现类似的变化趋势.这个观察结果表明：虽然增大K值可以使得隐藏特征向量的表示能力增强，但是同时也会带来一些问题，即，增加模型参数数量，引入一些噪音，从而降低兴趣点推荐算法的准确性.这个观察结果再次验证了矩阵分解模型的基本假设：仅有少量的隐藏因子影响用户的偏好和刻画兴趣点的特征.

5　结　　论

随着移动设备和GPS等技术的发展，基于位置的社交网络变得越来越普遍.兴趣点推荐是基于位置社交网络中的重要组成部分，可以满足用户个性化需求，减轻信息过载问题.为了解决传统兴趣点推荐算法中存在的问题，本文提出了基于Ranking的泊松矩阵分解兴趣点推荐算法.针对基于位置社交网络中用户的签到行为特点，利用泊松分布模型替代高斯分布模型建模用户在兴趣点上签到行为，然后采用BPR标准优化泊松矩阵分解的损失函数，拟合用户在兴趣点对上偏序关系.最后，为了进一步改进推荐算法的性能，利用包含地域影响力的正则化因子约束泊松矩阵分解的过程.在真实数据集上的实验结果表明，本文提出基于Ranking的泊松矩阵分解兴趣点推荐算法的性能优于传统的兴趣点推荐算法.

近年来，深度学习[25]在计算机视觉和自然语言处理等领域表现出巨大的潜力，而且已有研究者将深度学习技术与传统协同过滤技术相结合，以改善传统推荐算法的性能，如文献[26-27]等.将深度学习技术与本文提出的兴趣点推荐算法相结合将是一个有趣的研究方向.另外，用户在不同的时间段可能表现出不同的签到行为，因此，在本文提出的兴趣点推荐算法基础上考虑时间因素也是本文未来的研究方向.

[1]Adomavicius G, Tuzhilin A. Toward the next generation of recommender systems: A survey of the state-of-the-art and possible extensions[J]. IEEE Trans on Knowledge and Data Engineering, 2005, 17(6): 734-749

[2]Pan R, Zhou Y, Cao B, et al. One-class collaborative filtering[C] //Proc of the 8th IEEE Int Conf on Data Mining (ICDM’08). Los Alamitos, CA: IEEE Computer Society, 2008: 502-511

[3]Hu Y, Koren Y, Volinsky C. Collaborative filtering for implicit feedback datasets[C] //Proc of the 8th IEEE Int Conf on Data Mining (ICDM’08). Los Alamitos, CA: IEEE Computer Society, 2008: 263-272

[4]Tobler W R. A computer movie simulating urban growth in the Detroit region[J]. Economic Geography, 1970, 46: 234-240

[5]Yang B, Lei Y, Liu D, et al. Social collaborative filtering by trust[C] //Proc of the 23rd Int Joint Conf on Artificial Intelligence (AAAI’13). Menlo Park, CA: AAAI Press, 2013: 2747-2753

[6]Guo G, Zhang J, Yorke-Smith N. Trustsvd: Collaborative filtering with both the explicit and implicit influence of user trust and of item ratings[C] //Proc of the 29th AAAI Conf on Artificial Intelligence (AAAI’15). Menlo Park, CA:AAAI Press, 2015:123-129

[7]Ma H, Yang H, Lyu M R, et al. Sorec: Social recommendation using probabilistic matrix factorization[C] //Proc of the 17th ACM Conf on Information and Knowledge Management (CIKM’08). New York: ACM, 2008: 931-940

[8]Jamali M, Ester M. A matrix factorization technique with trust propagation for recommendation in social networks[C] //Proc of the 4th ACM Conf on Recommender Systems (RecSys’10). New York: ACM, 2010: 135-142

[9]Ye M, Yin P, Lee W C. Location recommendation for location-based social networks[C] //Proc of the 18th SIGSPATIAL Int Conf on Advances in Geographic Information Systems. New York: ACM, 2010: 458-461

[10]Ye M, Yin P, Lee W C, et al. Exploiting geographical influence for collaborative point-of-interest recommendation[C] //Proc of the 34th Int ACM SIGIR Conf on Research and Development in Information Retrieval (SIGIR’11). New York: ACM, 2011: 325-334

[11]Breese J S, Heckerman D, Kadie C. Empirical analysis of predictive algorithms for collaborative filtering[C] //Proc of the 14th Conf on Uncertainty in Artificial Intelligence (UAI’98). San Francisco, CA: Morgan Kaufmann, 1998: 43-52

[12]Cheng C, Yang H, King I, et al. Fused matrix factorization with geographical and social influence in location-based social networks[C] //Proc of the 26th AAAI Conf on Artificial Intelligence (AAAI’12). Menlo Park, CA: AAAI Press, 2012:17-23

[13]Zhang J D, Chow C Y. GeoSoCa: Exploiting geographical, social and categorical correlations for point-of-interest recommendations[C] //Proc of the 38th Int ACM SIGIR Conf on Research and Development in Information Retrieval (SIGIR’15). New York: ACM, 2015: 443-452

[14]Liu Y, Wei W, Sun A, et al. Exploiting geographical neighborhood characteristics for location recommendation[C] //Proc of the 23rd ACM Int Conf on Information and Knowledge Management (CIKM’14). New York: ACM, 2014: 739-748

[15]Lian D, Zhao C, Xie X, et al. Geomf: Joint geographical modeling and matrix factorization for point-of-interest recommendation[C] //Proc of the 20th ACM SIGKDD Int Conf on Knowledge Discovery and Data Mining (KDD’14). New York: ACM, 2014: 831-840

[16]Rendle S, Freudenthaler C, Gantner Z, et al. BPR: Bayesian personalized ranking from implicit feedback[C] //Proc of the 25th Conf on Uncertainty in Artificial Intelligence (UAI’09). Arlington, VA: AUAI Press, 2009: 452-461

[17]Sarwar B, Karypis G, Konstan J, et al. Item-based collaborative filtering recommendation algorithms[C] //Proc of the 10th Int Conf on World Wide Web (WWW’01). New York: ACM, 2001: 285-295

[18]Levandoski J J, Sarwat M, Eldawy A, et al. Lars: A location-aware recommender system[C] //Proc of the 28th Int Conf on Data Engineering (ICDE’12). Los Alamitos, CA: IEEE Computer Society, 2012: 450-461

[19]Yuan Q, Cong G, Ma Z, et al. Time-aware point-of-interest recommendation[C] //Proc of the 36th Int ACM SIGIR Conf on Research and Development in Information Retrieval (SIGIR’13). New York: ACM, 2013: 363-372

[20]Koren Y, Bell R, Volinsky C. Matrix factorization techniques for recommender systems[J]. Computer, 2009 , 42(8): 30-37

[21]Mnih A, Salakhutdinov R. Probabilistic matrix factorization[C] //Proc of the 21st Annual Conf on Neural Information Processing Systems (NIPS’07). New York: Curran Associates, 2007: 1257-1264

[22]Liu B, Fu Y, Yao Z, et al. Learning geographical preferences for point-of-interest recommendation[C] //Proc of the 19th ACM SIGKDD Int Conf on Knowledge Discovery and Data Mining (KDD’13). New York: ACM, 2013: 1043-1051

[23]Gao Rong, Li Jing, Du Bo, et al. A synthetic recommendation model for point-of-interest on location-based social networks: Exploiting contextual information and review[J]. Journal of Computer Research and Development, 2016, 53(4): 752-763 (in Chinese)

(高榕, 李晶, 杜博, 等. 一种融合情景和评论信息的位置社交网络兴趣点推荐模型[J]. 计算机研究与发展, 2016, 53(4): 752-763)

[24]Ma H, Liu C, King I, et al. Probabilistic factor models for web site recommendation[C] //Proc of the 34th Int ACM SIGIR Conf on Research and Development in Information Retrieval (SIGIR’11). New York: ACM, 2011: 265-274

[25]LeCun Y, Bengio Y, Hinton G. Deep learning[J]. Nature, 2015, 521(7553): 436-444

[26]Wang H, Wang N, Yeung D Y. Collaborative deep learning for recommender systems[C] //Proc of the 21st ACM SIGKDD Int Conf on Knowledge Discovery and Data Mining (KDD’15). New York: ACM, 2015: 1235-1244

[27]Li S, Kawale J, Fu Y. Deep collaborative filtering via marginalized denoising auto-encoder[C] //Proc of the 24th ACM Int Conf on Information and Knowledge Management (CIKM’15). New York: ACM, 2015: 811-820

Yu Yonghong, born in 1978. PhD candidate and lecturer. His main research interests include recommendation algorithm and social network analysis (yuyh@njupt.edu.cn).

Gao Yang, born in 1972. Professor and PhD supervisor. His main research interests include reinforcement learning and machine learning (gaoy@nju.edu.cn).

Wang Hao, born in 1983. PhD and assistant researcher. His main research interests include recommendation algorithm and reinforcement learning (wanghao.hku@gmail.com).

2014年《计算机研究与发展》高被引论文TOP10

数据来源：中国知网, CSCD；统计日期：2016-02-16

A Ranking Based Poisson Matrix Factorization Model for Point-of-Interest Recommendation

Yu Yonghong, Gao Yang, and Wang Hao

(StateKeyLaboratoryforNovelSoftwareTechnology(NanjingUniversity),Nanjing210023) (CollaborativeInnovationCenterofNovelSoftwareTechnologyandIndustrialization,Nanjing210023)

With the rapid growth of location-based social network (LBSN), point-of-interest (POI) recommendation has become an important means to meet users’ personalized demands and alleviate the information overload problem. However, traditional POI recommendation algorithms have the following problems: 1)most of existing POI recommendation algorithms simplify users’ check-in frequencies at a location, i.e., regardless how many times a user checks-in a location, they only use binary values to indicate whether a user has visited a POI; 2)matrix factorization based POI recommendation algorithms totally treat users’ check-in frequencies as ratings in traditional recommender systems and model users’ check-in behaviors using the Gaussian distribution; 3)traditional POI recommendation algorithms ignore that users’ check-in feedback is implicit and only positive examples are observed in POI recommendation. In this paper, we propose a ranking based Poisson matrix factorization model for POI recommendation. Specifically, we first utilize the Poisson distribution instead of the Gaussian distribution to model users’ check-in behaviors. Then, we use the Bayesian personalized ranking metric to optimize the loss objective function of Poisson matrix factorization and fit the partial order of POIs. Finally, we leverage a regularized term encoding geographical influence to constrain the process of Poisson matrix factorization. Experimental results on real-world datasets show that our proposed approach outperforms traditional POI recommendation algorithms.

location-based social network (LBSN); point-of-interest (POI) recommendation; Poisson matrix factorization; Bayesian personalized ranking (BPR) metric; geographical influence

2016-03-21；

2015-05-24

国家自然科学基金项目(61432008,61175042,61403208)

TP181

This work was supported by the National Natural Science Foundation of China (61432008, 61175042, 61403208).