IncPR：一种基于增量计算的并行PageRank算法

姜双双　廖　群　杨愚鲁　李　涛

(南开大学计算机与控制工程学院　天津　300350)



IncPR：一种基于增量计算的并行PageRank算法

姜双双廖群杨愚鲁李涛

(南开大学计算机与控制工程学院天津300350)

(highfly@mail.nankai.edu.cn)

广泛的互联网的商业应用使PageRank算法有重要地位.网络规模不断地增大，同时网络变化带来的时效性要求，也使PageRank计算对计算资源的要求不断地提高.为降低该问题对计算资源的消耗水平，降低计算成本，一种基于增量计算思想的PageRank算法：IncPR被提出.IncPR通过重用已有的结果，增量地获得数据变化后的结果.该算法在并行计算环境中，能够有效地降低计算量，缩短计算时间.理论分析表明，该算法计算结果的误差范围与蒙特卡罗PageRank算法相当，其时间复杂度优于其他已有的相关算法，且不引入额外的存储开销.在分布式集群Hama上进行的实验验证了理论分析的结果，IncPR在得到与蒙特卡罗PageRank算法同等(甚至更高)结果精度的情况下，显著地降低了计算量.

PageRank；Web数据挖掘；增量计算；蒙特卡罗算法；并行与分布式处理

随着电子商务、物联网、社交网络、生物信息学等诸多领域的蓬勃发展，大量有价值的数据快速地产生并积累，“大数据”的计算处理成为近年来的研究热点之一.大量的统计结果显示，大数据应用问题普遍具有数据的总量大且增长速度快的特点[1].截止到2016年3月，Google抓取的网页已超过60万亿，并以每天超过450亿个网页的速度增长[2-3]；FaceBook的用户数量已达到13亿并保持每秒5位用户的增长速度[4].当数据发生变化时，需要对数据重新处理以更新结果，因此，高效地处理频繁变化的大数据具有重大意义.

PageRank[5]算法在搜索引擎、信息检索、社交网络挖掘等多个领域得到广泛的应用，具有重要地位.PageRank算法所处理的互联网络和社交网络数据是典型的频繁变化的大数据集，具有总量大、更新速度快、每次更新的数据占总量比例小的特点.为满足结果的时效性要求，只要数据更新就需要重计算以更新结果.在频繁变化的大数据集上反复地进行PageRank计算，会消耗巨大的计算资源，计算成本高.

尽管以MapReduce[6],Spark[7]及Pregel[8]集群等为代表的分布式计算技术、以及很多并行PageRank算法[9-11]能够提高PageRank的计算速度.但这些技术仍不能有效地降低反复计算带来的高资源消耗和高计算成本.

因此针对这一问题本文通过扩展一种典型的PageRank计算算法——蒙特卡罗算法[12]，提出了一种基于增量计算的PageRank算法——IncPR.当数据集发生变化时，IncPR利用的是已有的PageRank计算结果，不需要保存其他历史数据，没有引入额外的存储开销；在进行处理时，IncPR根据数据的变化情况在已有的计算结果上增量地进行更新，获得新数据集的结果，这有效地降低了计算量，提高了计算效率.此外，IncPR能高效处理网页增加、减少、网页链接关系变更等多种情况，这也是其较之于部分相关增量算法的优势之一.

理论分析证明，IncPR得到结果的误差范围和蒙特卡罗PageRank算法得到的结果误差范围的量级相当，即IncPR具有与蒙特卡罗PageRank算法相同的正确性.在增加m个节点和n条边的情况下，IncPR的时间复杂度为O((cm+n)Rc2)，其中参数c和R分别代表蒙特卡罗方法的停止概率和启动次数.IncPR的时间复杂度优于其他已有的增量PageRank算法.在分布式集群Hama[13]上进行的实验验证了理论分析的结果，实验数据表明在得到与蒙特卡罗PageRank算法同等(甚至更高)精度结果的情况下，IncPR显著地降低了计算量.

综上，本文工作的贡献有3点：

1) 提出了一种基于增量计算的PageRank算法IncPR.通过在已有结果的基础上，增量地更新得到新结果的方法，IncPR能有效地降低PageRank的计算量，且不引入额外的存储开销；

2) 通过理论分析证明了IncPR与蒙特卡罗PageRank算法的结果具有相等量级的精度，且时间复杂度优于已有的增量PageRank算法；

3) 在Hama集群上基于大规模真实图数据的大量实验，验证了IncPR的正确性和计算效率.IncPR在保证结果正确的前提下能有效降低PageRank的计算量.

1　相关工作

1.1PageRank算法

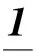
P=(1-c)Q+(cn)E；

(1)

(2)

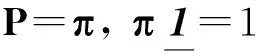
(3)

当前PageRank算法主要可以分成2类：线性代数方法和蒙特卡罗方法.前者利用线性代数方法根据式(3)求解π,PowerIteration[5]、Gauss-Southwell[14]、基于LUQR分解的PageRank算法[15]等是典型的线性代数计算方法.它们处理大规模矩阵效率高，且能够根据需要权衡结果精度和计算开销.蒙特卡罗方法[12,16-17]的基本思想是利用随机游走模拟大量用户随机访问网页的行为，并通过统计各节点的被访问次数估算PageRank的近似值.典型的蒙特卡罗方法[12]包括循环起点的全路径算法、随机起点的蒙特卡罗算法等.它们具有易于并行化的特点，且能够以较小的计算开销尽快地得到满足精度要求的近似结果.

相关的研究结论已证明[12]相较于其他蒙特卡罗算法，循环起点的全路径蒙特卡罗算法具有更高的计算效率，因此在已有PageRank算法优化研究[18]中常被作为算法改进的基础.该算法的计算方法更适于引入增量计算的思想.本文工作也将循环起点的全路径算法作为蒙特卡罗算法的代表，简称为基准蒙特卡罗算法，用BasicPR表示.BasicPR计算PageRank的方法是由每个节点为起点启动R个随机游走过程，随机游走中的每一步以c的概率停止或走到等概率地随机选中的某个邻居节点，并以此选中的节点为起点继续这个随机游走过程.对于有n个网页的情形，共进行n×R次随机游走，当所有随机游走过程都停止时，统计任意节点u的访问次数VT(u)，用VT(u)除以所有节点的访问次数的总和，就得到节点u的PageRank的近似结果.通过增加R，BasicPR的结果可以足够接近PageRank的真实值.IncPR使用了和BasicPR相同的随机游走方法并在其基础上引入了增量计算思想加以改进.

1.2增量PageRank算法相关研究

为保证频繁变化的网络上获得满足时效性要求的PageRank值，通常需要反复进行PageRank计算，从而造成对计算资源的巨大消耗.为解决这一问题，一些改进的PageRank算法被提出.这些算法大致可以被归纳为4类:

1) 利用已有结果加速迭代收敛

Kamvar等人[19]提出了一种基于AitkenΔ2的推断方法加快收敛的算法,该算法的收敛效率受变化数据位置影响，效率的提升并不明显[18].Ohsaka等人[14]提出了一种通过重用已有结果的Guass-Southwell方法，该方法能够提升算法的收敛速度，但该算法并没有讨论节点变化的情况的处理方法.

2) 控制及利用变化的数据的影响范围

此类算法[20-23]通常将整个图按照某种策略划分成若干相互连通的子图，当某个子图内发生变化时，算法尽量将计算操作控制在子图内部，对其他子图不产生影响或影响较小，从而达到降低计算量的目的.它们的局限性在于算法的表现受图结构的影响较大，且维护有效的图划分也比较困难.

3) 基于蒙特卡罗方法的增量改进

与线性代数方法相比，蒙特卡罗方法显然更易于按照增量计算的思想进行改进[12].Bahmani等人提出算法[18]保存之前的随机游走路径，当数据发生变化时，根据图的变化情况对随机游走路径进行部分更新.Bahmani的算法假设图中的边随机地逐条到达，每当一条边到达即进行计算，当累计增加n条边时，处理包含|V|个节点的图数据，该算法的时间复杂度为O(|V|lnnc2).Lofgren等人[24]在Bahmani等人工作[18]的基础上，对算法复杂度的分析进行了补充.该算法是一种高效的增量PagaRank算法，能有效应对节点和边发生变化的情况，但其保存随机游走路径的历史数据的做法也引入了较大的存储开销.

4) 其他方法

Tong等人[25]提出了一种适合于二分图的更新PageRank值的方法，该方法在|V|×l的图上能够获得O(l2)的时间复杂度，然而互联网和社交网络中的l=|V|，当n条边到达时，更新的代价为O(n|V|2)，并不适合扩展到大规模图数据中来.Mcsherry等人[26]将多种启发算法应用到迭代算法中，以增量的更新操作计算流数据上的PageRank值，但该算法在控制计算量的情况下不能保证结果精度.

综上，已有的增量PageRank算法，都需要消耗额外的存储空间.本文提出的IncPR并不需要额外的存储空间，且相较于已有的高效增量PageRank算法，IncPR的时间复杂度更低，在计算效率和存储开销2个方面优势明显.

2　增量PageRank计算模型

为降低频繁变化的海量数据集上反复计算PageRank的资源消耗，节约计算成本，本文提出了一种增量PageRank算法——IncPR.本节首先以一个示例介绍基于增量计算思想的PageRank计算方法，接着给出IncPR的计算模型的形式化概述.

2.1增量PageRank计算示例

增量PageRank计算将每一次数据更新作为一个新时刻.假设时刻t图G形如图1(a)所示，其中实线表示时刻t-1的图数据，虚线表示的边e3,5是在时刻t新增加的.图1(b)表示时刻t-1使用BasicPR得到的随机游走路径的集合.

在使用BasicPR计算时刻t的图数据时，节点5在随机游走中被访问的机会较时刻t-1增大.如果以图1(b)所示的随机游走路径当作时刻t的初始路径，那么仅需要更改部分路径(每次访问节点3后的随机游走路径)即可以得到符合时刻t各节点的被访问概率的随机游走路径.即每当遇到随机游走路径中出现节点3，即按照时刻t的图，为节点3重新选择下一步的节点，并更新之后的随机游走路径.这样即可得到如图1(c)所示的随机游走路径.尽管这个集合是由图1(b)变化来的，但该集合中各节点被访问的概率和在时刻t的图上重新产生的随机游走路径集合相等，其概率都是由图的拓扑特征和随机游走的停止概率参数共同决定的.

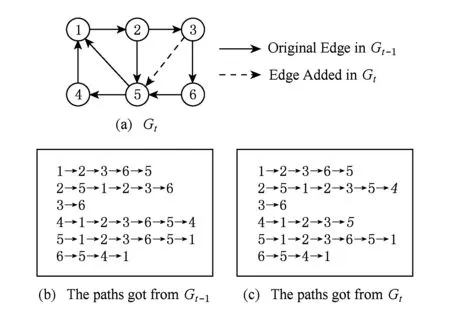
Fig. 1　An example of computing PageRank incrementally.图1　增量PageRank计算示例

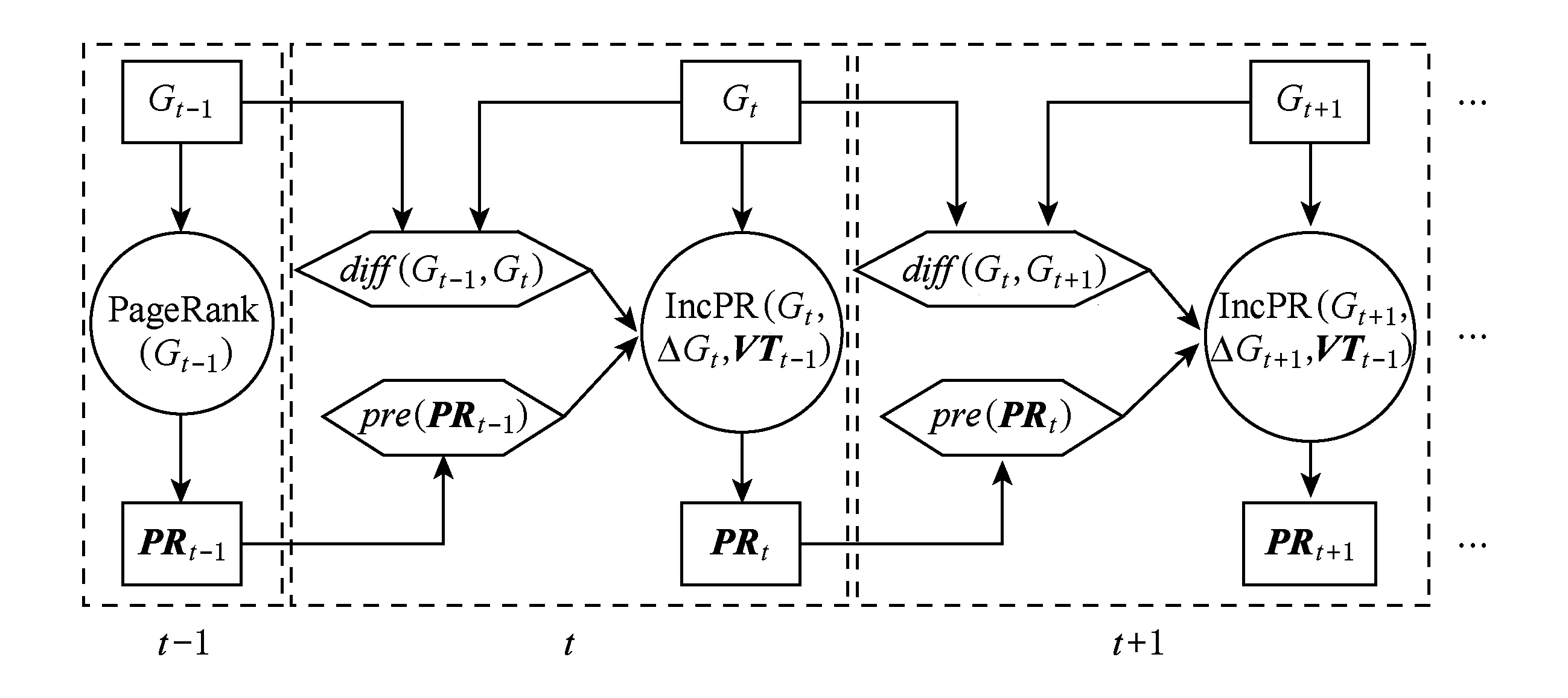
Fig. 2　Overview of incremental computation of PageRank.图2　增量PageRank计算模型

基于这种考虑，就可以将增量计算的思想引入PageRank的计算过程.以时刻t-1的BasicPR得到的随机游走路径为基础，在发生变化的边(或节点)所影响的路径上采用相同的随机游走过程更新随机游走路径，并重新计算PageRank得到新结果.这样的增量计算方式，避免了重新从头生成全图的随机游走路径，降低了计算量.这也是已有的基于蒙特卡罗方法的增量PageRank算法[12,18,24]的基本计算过程.此类算法能够降低PageRank的计算量，但需要较大的存储开销来保存随机游走路径.

而从节点的访问概率的角度观察，对时刻t的图进行计算时，与时刻t-1相比，每次访问节点3后，节点5被访问的概率增加，节点6被访问的概率减少，而且节点5被访问的概率的增加量和节点6减少的量基本相当.这一特点即是IncPR的设计基础之一.

2.2增量PageRank计算模型概述

IncPR是一种基于增量思想的PageRank算法，易于并行化实现.与已有的基于蒙特卡罗算法的增量PageRank算法不同，IncPR并不需要保存任何随机游走路径的历史信息.它利用之前一个时刻已经得到的PageRank向量，逆推得到蒙特卡罗模拟的节点访问次数统计，结合图数据的变化情况，增量地更新得到新图上的节点访问次数统计，进而更新PageRank的计算结果.

IncPR的计算过程借助于这样的事实，即蒙特卡罗算法中节点的访问次数的期望具有稳定性[11]，来保证其正确性(相关证明见4.1节).IncPR的计算过程本质上与2.1节中的增量计算过程类似，即以受增量影响的任意节点v为起点，生成若干新路径片段，并用新路径片段替换旧路径片段的过程.

IncPR能有效地处理图中节点和边的增加与删除的情况，且由于能较大程度地利用之前的结果，降低重复计算，因此该算法能够有效地减少图数据变更后重计算PageRank值的计算量.

IncPR在变化的图数据上进行增量的Page-Rank计算的过程，可以形式化地描述为以下的增量计算工作模型，如图2所示.对于图G(V,E),令时刻t图的快照为Gt(Vt,Et).图的变化部分ΔGt=diff(Gt-1,Gt)={ΔVt,ΔEt}.相应地，从Gt得到的PageRank结果记作PRt.IncPR假设ΔGt已知，PRt-1已知，并通过预处理操作pre(PRt-1)得到BasicPR处理Gt-1时得到的所有节点的访问次数的集合VTt-1.

IncPR算法以Gt,ΔGt和VTt-1为输入，在VTt-1的基础上，结合Gt,ΔGt采用改进的蒙特卡罗方法增量地更新ΔGt对于PageRank新值的影响，最终得到新的PageRank计算结果PRt.一般使用Xt代表符号X在时刻t对应的对象集合，而使用|X|代表集合X的元素的个数.

VTt=SVTt×PRt.

(4)

预处理可以按照式(4)的方式求得VTt-1.其中，SVTt是时刻t的蒙特卡罗模拟中所有节点访问次数的总和，SVTt=|Vt|Rc.值得注意的是，式(4)具有普遍性，即使PRt-1并不是通过蒙特卡罗方法得到，也可以通过式(4)得到VTt-1.也就是说IncPR可以利用任意PageRank算法得到的结果.

3　IncPR：增量PageRank算法

IncPR通过重用当前已有的计算结果初始化节点的访问次数，根据图数据的变化对最终结果进行计算.对于图数据变化的不同情况，采用不同的计算策略.本文将图的变化分为2种情况：1)边的变化,仅有边的增加和删除；2)点的变化,节点和边均有增加和删除.本节将分别介绍对这2种情况的处理方法.

3.1IncPR处理边的变化

IncPR处理边的变化时采取2个主要步骤:

1) 对于每条变化的边，按一定策略更新某些节点的访问次数；

2) 访问次数被更新的节点，按照访问次数的更新量进行若干次随机游走，将新生成的随机游走路径上的节点的访问次数(依据一定的原则)增或减1.

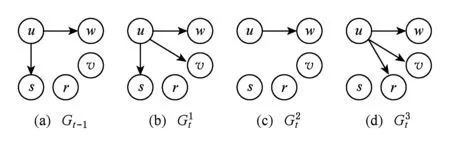
Fig. 3　Three cases of changing edges.图3　边变化的3种情况

图3展示了一个节点上边的变化的3种典型情况(与边的变化无关的节点和边被省略)，图3(a)表示时刻t-1的图数据Gt-1.图3(b)(c)(d)表示时刻t的图数据Gt，分别描绘了增加一条边、删除一条边、同时增加删除多条边的示例.

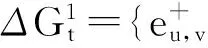
为了利用时刻t-1的访问次数得到时刻t的结果，节点v的访问次数需要加上期望的变化量，节点w,s的访问次数平均分摊VT(v)t的增加量，作为各自访问次数的减少量.当VT(v)t,VT(w)t和VT(s)t都更新完毕，则按照步骤2操作，s,v和w分别进行与各自访问次数更新数量相等的随机游走，从v发出的新随机游走路径上的节点的访问次数增1，表示新路径的添加；从s和w发出的新随机游走路径上的节点将访问次数减1，表示旧路径的删除.上述操作的结果等价于经过节点u的部分路径被新路径替换.总体上看，上述操作相当于由于边的增加，以s,v和w三节点为起点的随机游走路径中，从u获得的访问次数的重分配，重分配的结果与在图Gt上重新进行随机游走分配节点u发出访问的情况相当.

边删除情况与边增加情况的处理办法类似.区别仅在于访问次数的增减数量和操作顺序.如图3(a)(c)所示，当边eu,s被删除时，节点s的访问次数VT(s)t减少，减少量的期望等于(1-c)×VT(u)t-1|S(u)t-1|,相应的节点w的访问次数VT(w)t增加，增加量的期望等于VT(s)t的减少量.之后，分别以w,s为起点进行对应数量的随机游走，来更新节点w,s的变化对其子节点的影响.以w,s为起点的随机游走经过的节点分别进行加1和减1的操作表示新路径的生成和旧路径被替换.

结合边的增加和删除的情况，可以得到更一般化的处理方法.令eu,x表示变化(增加或删除)的边，M代表VT(x)t变化量的大小,对于u的其他邻居y，令N代表VT(y)t变化量的大小，如式(5)(6)所示:

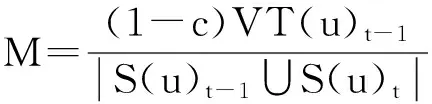
(5)

(6)

图3(d)反映了在时刻t分别增加和删除多条边的情况.由蒙特卡罗方法的计算特点可知，多条边分别增加和删除的情况，可以视作多次发生增加单条边和删除单条边的情况，按照上述处理单条边增加和删除的办法依次处理即可.

算法1使用伪代码描述了IncPR针对图中边的变化的处理逻辑.

算法1.ProcessIncEdges(Gt,diff(Gt-1,Gt),VTt-1,c).

输入：Gt={Et,Vt}表示时刻t的图数据、diff(Gt-1,Gt)={diff(E)+,diff(E)-}代表时刻t-1到时刻t图数据的变化量(边的增加和删除)、VTt-1代表时刻t-1的节点访问次数的集合、c是随机游走的停止概率；

输出：VTt为图Gt的节点访问次数的集合.

① 初始化VTt=VTt-1;

②ListSRW_Array〈node,count,tag〉;

③foreu,v∈diff(Gt-1,Gt)do

④ 由式(5)(6)计算M,N；

⑤ifeu,v∈diff(E)+do

⑥ SRW_Array.add(v,M,+);

⑦forw∈S(u)t-1do

⑧ SRW_Array.add(w,N,-);

⑨endfor

⑩else

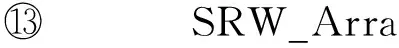
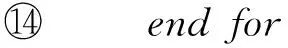
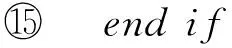
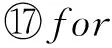
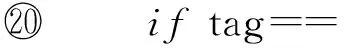
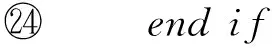
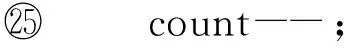
3.2IncPR处理点的变化

节点的增加通常伴随边的增加，可分为新增节点有入边和无入边2种情况讨论.如果新增加的节点没有入边，则只要按照与时刻t-1相同的随机游走方法补上R次以新节点为起点的随机游走，再更新节点的PageRank值即得到最终结果.但如果新增节点有入边，则需要在上述处理的基础上按照3.1节的方法处理.如图4所示，图4(a)(b)分别表示时刻t-1和时刻t的图数据，这种情况可以视作2个过程的叠加：先增加一个节点和节点的出边，得到如图4(c)所示的过渡图数据和对应的PageRank结果；再增加节点的入边.

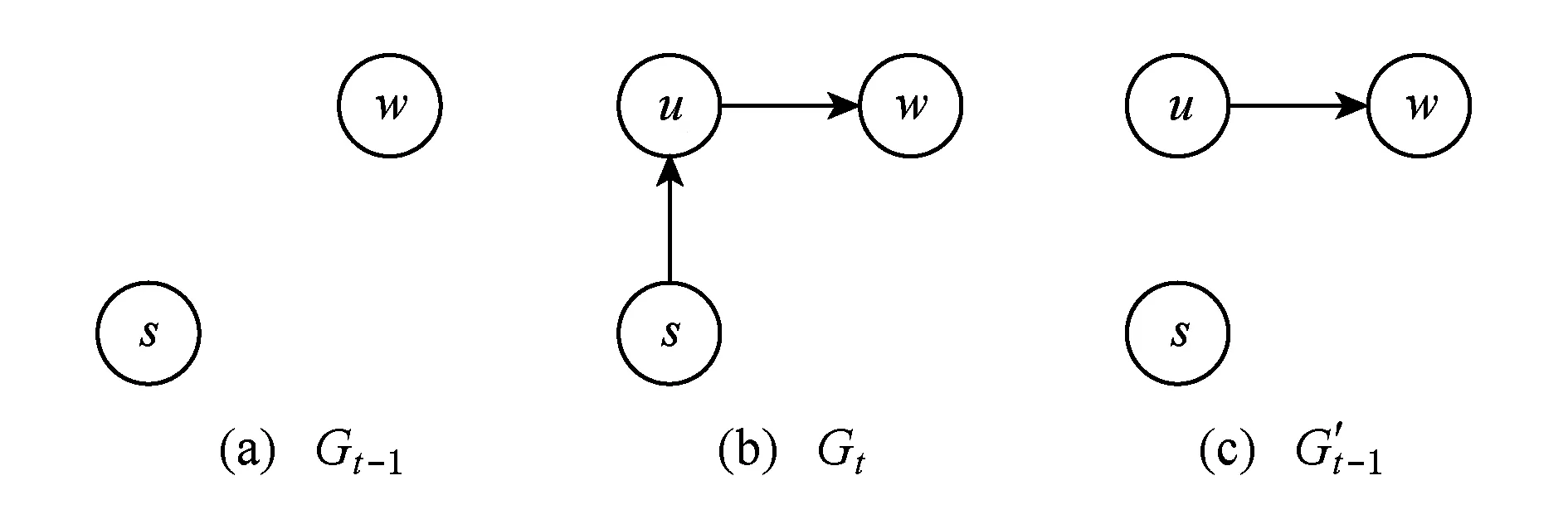
Fig. 4　An example of disassembly of adding a node.图4　节点增加等价于节点和边分别增加

类似地，节点的删除则可以看作2个过程：节点的删除和与节点相连边的删除.而稍有不同的是，对于删除节点的情况，只需对变化的边按照3.1节中的方法处理，而不需要再重复地减去R次以被删除节点为起点的随机游走对其他节点的影响，这个操作的影响在处理被删除的边时已被处理.

综上，本文提出的IncPR可以概括为2个步骤：1)处理新增节点和节点的出边；2)按照3.1的方法处理变化的边.算法2为IncPR的伪代码描述.

算法2.IncPR(Gt,diff(Gt-1,Gt),VTt-1,c,R).

输入：Gt={Et,Vt}表示时刻t的图数据、diff(Gt-1,Gt)={diff(E)+,diff(E)-,diff(V)+,diff(V)-}为时刻t-1到时刻t图数据的变化量(边和节点的增加和删除)、VTt-1为时刻t-1得到的被访问次数的集合、c是随机游走的停止概率、R是各节点开始的随机游走次数;

输出：PRt为图Gt的PageRank向量.

① 初始化VTt=VTt-1;*新增节点的访问次数为0*

②foru∈diff(V)+do

③ count=R;

④whilecount>0do

⑤ 以u为起点进行停止概率为c的随机游走，得到随机游走路径L;

⑥ 对任意节点yinL，VT(y)t++;

⑦ count--;

⑧endwhile

⑨endfor

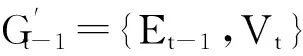
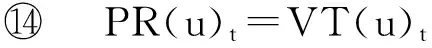
4　算法正确性及时间复杂度分析

4.1算法的正确性证明

IncPR是一种增量的蒙特卡罗模拟算法，基于模拟的PageRank算法得到的结果是近似值.类似于文献[11,18]中对BasicPR正确性的证明，本文证明了IncPR与BasicPR计算得的节点的访问次数的期望相等且IncPR计算得到节点的访问次数与真实的访问次数足够接近,这样即证明IncPR是正确的.

定理1. 对于任意节点v, 在图Gt上使用IncPR得到的访问次数的期望E[VT(v)IncPR]，与使用BasicPR计算得到的访问次数的期望E[VT(v)BasicPR]相等.

证明.IncPR在进行计算时，利用图Gt-1的访问次数初始化Gt中节点的访问次数，初始化的结果可以看作是从|Vt-1|个节点出发每个节点进行R次随机游走得到的|Vt-1|R条路径.对于每一个变化的边eu,v，IncPR会从节点u的子路径中选出M条旧的子路径，并生成M条新的子路径替换旧路径.此操作并没有改变总路径的起点和数量；对于每个变化的节点，IncPR沿用BasicPR从每个节点进行R次随机游走.因此，IncPR处理完Gt后，可以看作得到与BasicPR起点相同且对应起点数目相同的路径.

使用BasicPR计算图Gt的PageRank值时，图中任意节点v的访问次数的期望为

(7)

其中，Pu,v表示以节点u为起点的随机游走路径经过节点v的概率，αu表示以节点u为起点的随机游走次数，由于2种算法每个节点都进行了R次随机游走，故任意节点u的αu=R.从节点u出发的随机游走路径经过节点v的概率Pu,v是由每一条从节点u到节点v的路径的概率累加得到的，如式(8)所示:

(8)

其中,qi j(i=u,w,…,y;j=w,x,…,v)如式(2)所示，表示节点u到节点w的跳转概率，节点u选取某一条路径访问节点v的概率为该路径上从u到v经过的节点间的跳转概率的乘积.BasicPR在进行随机游走时，任意节点间的跳转概率只与图结构有关，若节点u，w之间存在连边，则qu,w=(1-c)|S(u)|；IncPR在进行随机游走时，对于出边发生变化的节点u，该节点的访问次数按照期望值在子节点之间均匀分配，节点u到任意子节点的跳转概率为(1-c)|S(u)|，这些节点与子节点间的跳转概率与BasicPR中的相同；其他节点间的跳转概率按照qu,w进行处理，与BasicPR相等.因此，IncPR在得到|Vt|R条路径时，任意节点间的跳转概率均与BasicPR相同.2种算法在计算图Gt的PageRank值时，任意节点间的Pu,v相等.

综上，IncPR算法与BasicPR在计算相同图数据的PageRank值时，任意节点的访问次数的期望相等，定理1得证.

证毕.

定理2. 对于任意节点v, 在图Gt上使用IncPR得到的节点v的PageRank值与节点v的PageRank的真实值非常接近，即有式(9)成立:

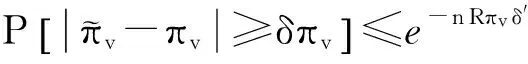
(9)

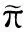
证明. 先讨论R=1的情况(R>1的情况同理可证).假设随机变量Xu是由u出发的随机游走路径上节点v的访问次数的c倍.Yu是这条随机游走路径的长度.令Wu=cYu，xu=E[Xu].由于对于不同的节点u随机变量Xu相互独立，则有：

(10)

显然有：0≤Xu≤Wu，E[Wu]=1.

则由期望的定义可知：

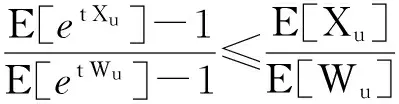
(11)

进而得到：

E[et Xu]≤xuE[et Wu]+1-xu=

xu(E[et Wu]-1)+1.

(12)

由于对任意的y有1+y≤ey，因此可得到：

E[et Xu]≤e-xu(1-E[et Wu]).

(13)

由马尔可夫不等式，可以得到：

(14)

类似地可以证明：

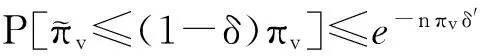
(15)

则定理2得证.

证毕.

综合定理1，2可知，IncPR得到的计算结果能够确保与BasicPR得到的结果同等正确.BasicPR计算PageRank的结果正确性在文献[12]中已被证明，因此IncPR也具有与BasicPR同等的正确性.

4.2算法的时间复杂度分析

本节通过分析IncPR的处理过程，推导出其时间复杂度.使用IncPR计算PageRank向量时，对于每一个增加的节点，算法都会以该节点为起点进行R次随机游走；对于每一个变化的边eu,v，都会以v为起点进行M次随机游走，作为新的子路径；同时，会以u的其他子节点为起点进行M次随机游走，作为待被替换子路径.一条变化的边需要进行2M次随机游走，以更新结果.

因此，假设Gt在Gt-1的基础上增加了m个节点且增加和删除了共计n条边，则增量算法需要进行随机游走的总次数TotalRW满足式(16)，其中M按式(5)求得.

(16)

令TotalComp表示IncPR的计算量大小，则有式(17)，其中E[X]代表随机游走路径长度的期望值.

TotalComp=TotalRW×E[X].

(17)

由于图中所有节点至少包含一个出边(悬挂点被看作包含|Vt|个出边)，发生变化边的起点至少增加或删除了一条边.因此对于任意变化的边eu,v的起点u，有：

|S(u)t-1∪S(u)t|≥2，

(18)

因此，可进一步推导出：

(19)

(20)

令E[VT]表示节点访问次数的均值.节点访问次数与节点总数的乘积为总的访问次数，总的访问次数等于随机游走路径总长度，故E[VT]=RE[X].由于随机游走路径长度服从参数为c的几何分布，故E[X]=1c，E[VT]=Rc.因此有:

TotalComp≤Rmc+Rnc2.

(21)

当图G发生变化的增量包含m个节点和n条边时，IncPR算法根据图G的中间数据更新结果的时间复杂度为O((cm+n)Rc2).

5　性能测试与分析

5.1实验设置

本文分别以Bahmani提出的增量PageRank算法[19]和BasicPR作为比较基准，对IncPR的结果正确性和计算量大小进行了实验.实验在基于BSP计算模型的Hama分布式计算框架[27]上实现了IncPR和上述2种对比算法.Hama的体系结构如图5所示.实验使用的Hama集群由6台同构节点组成，每个节点配备intel-i7 2600CPU、8GB内存、2TB磁盘，并通过千兆以太网连接.各节点安装Ubuntu14.04操作系统，主要的计算工具版本分别为Hama-0.6.4、zookeeper-3.4.6和Hadoop-1.2.1.

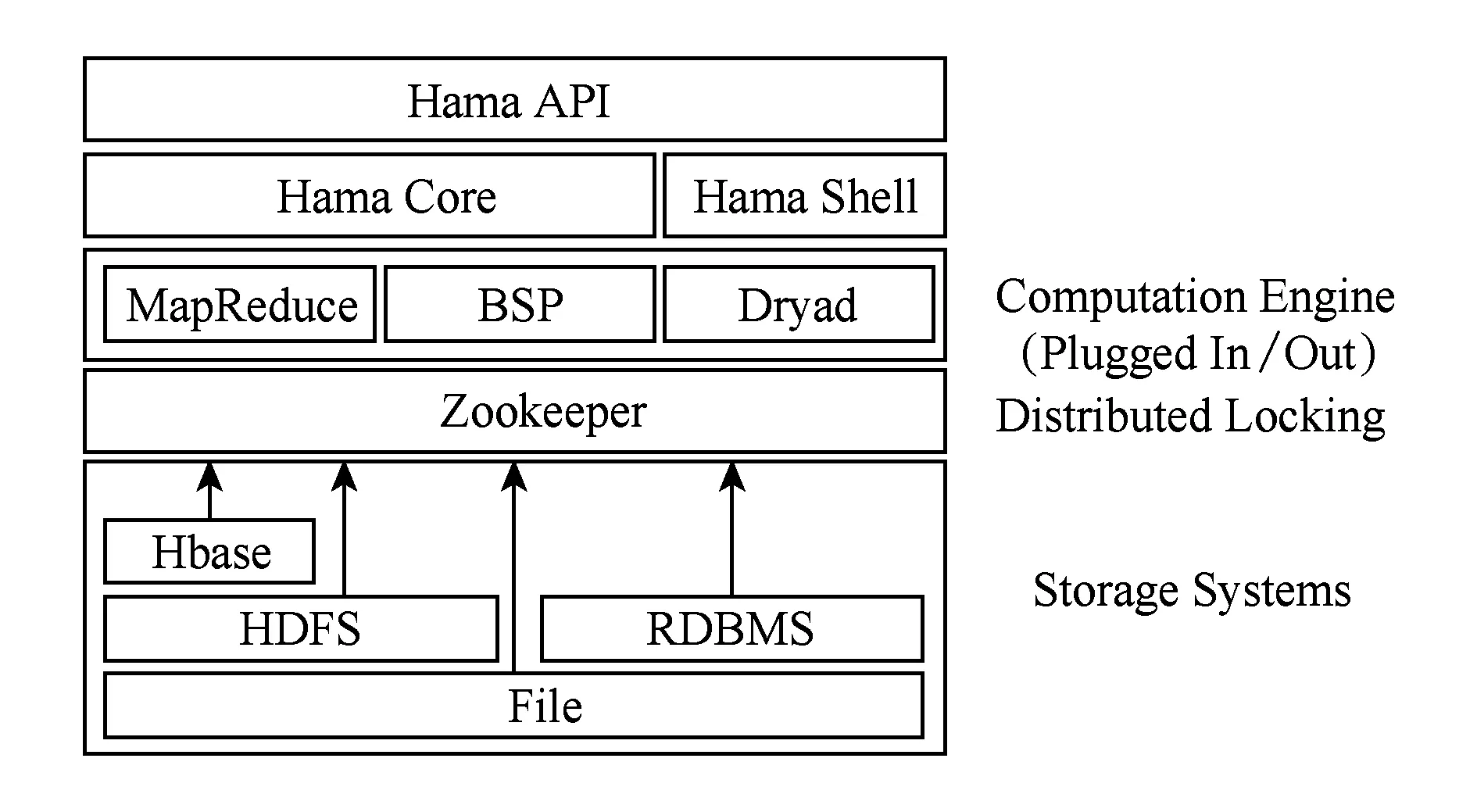
Fig. 5　Overview architecture of Hama.图5　Hama 分布式计算框架体系结构

实验使用了多组具有不同应用背景的真实数据集，对典型的数据集变化情况分别进行了多组实验，实验结果验证了IncPR的正确性和计算效率.权衡PageRank结果的精度和实验运行时间，实验选取参数R=20，c=0.15，默认情况下，初始的PageRank结果由该参数下的BasicPR计算得到.

5.2评价指标

实验主要从算法的结果精度和计算量2个方面考虑，选取了2个评价指标，以测试分析IncPR的正确性和计算效率.

1) 正确性指标

类似于已有的相关研究工作[10,14]，本文定义算法正确性的评价指标Err(Alg)如式(22).其中PR(u)代表由算法Alg得到的PageRank的计算结果，π(u)代表PageRank的真实值.显然地，Err(Alg)的大小代表了算法Alg的结果的相对精度.对于相同的图数据，Err(Alg)越小意味着算法得到的PageRank的计算结果的精度越高，即越接近真实的PageRank值.本文实验中PageRank的真实值由PowerIteration算法计算获得，参数ε=0.000 5.

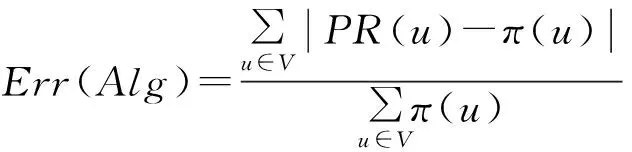
(22)

2) 计算量指标

本文定义Cost(Alg)作为算法计算效率的评价指标.基于蒙特卡罗的PageRank算法通过进行大量的随机游走来计算PageRank值，构造随机游走路径是此类算法的主要开销.由于随机游走中每一步的开销相同，算法的计算量可以由产生的随机游走的总步数表示.本文实验基于Hama框架实现，Page-Rank算法通过传递消息实现随机游走，通过统计消息通信的总数即得到随机游走的总步数.Cost(Alg)的值即等于算法在Hama框架上的发送的消息的总数.

5.3数据集及预处理

实验使用了多组不同的真实图数据集[28]，它们覆盖了从P2P网络到Web互联网和社交网络等多个不同应用领域.数据集的主要特征参数详见表1所示.类似于文献[10]中的做法，在不影响实验结果的准确性和算法计算量的前提下，实验对图数据进行了一定的预处理，将图中所有的单向边都改为双向边.

图数据的变化包括点和边的添加和删除共4种情况.由于增量算法在处理增加删除边的2种操作类似(区别仅是在进行随机游走时经过节点的操作)，因此实验仅测试添加点和边情况下算法的正确性和计算效率.仅增加边的实验中，先从原图中随机选择最多10%的边删除，将得到的图作为初始数据G，再从被删除边中，按固定比例(0.01%，0.05%，0.1%，0.5%，1%，5%，10%)随机添加到图G中作为变化后的图数据.增加点的实验，以原图为初始数据G，以G中的节点数为基准，生成固定比例(0.01%，0.05%，0.1%，0.5%，1%，5%，10%)的新节点并添加到G中，随机地为新节点选择一条入边和出边.

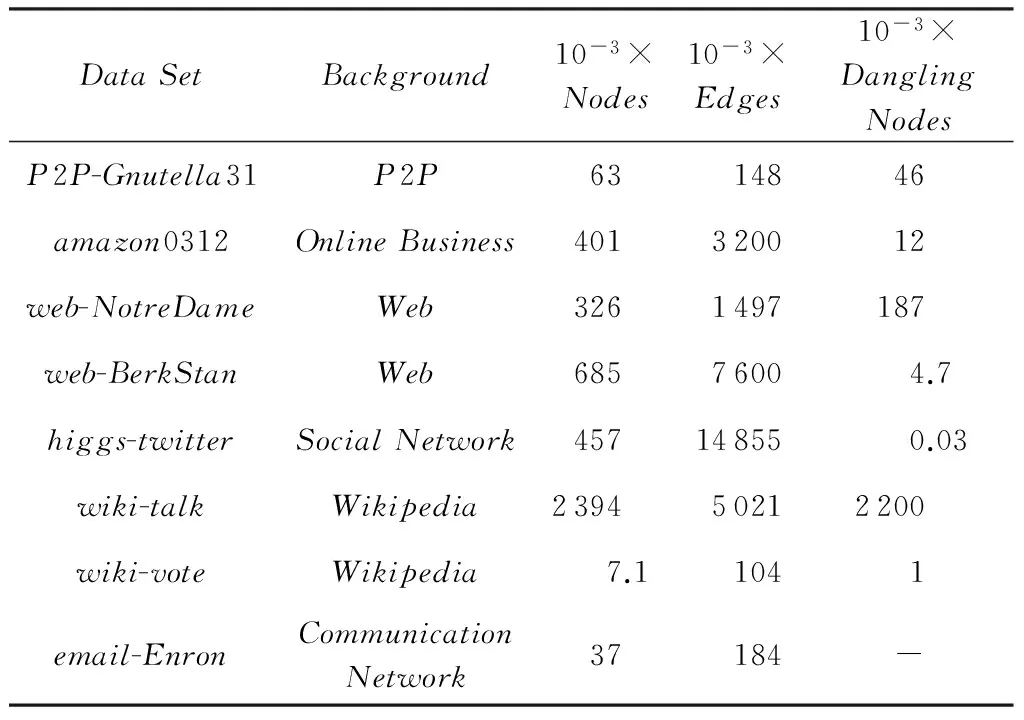
Table 1　Main Parameters of Data Sets表1　数据集的主要特征参数

5.4结果准确性

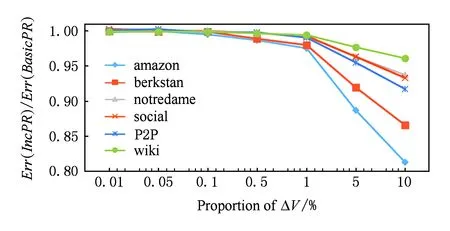
Fig. 6　Comparison of Err(Alg) with different proportion of ΔV.图6　增加不同比例的节点的误差比较

本节通过比较IncPR与Bahmani的增量算法和IncPR与BasicPR计算PageRank值的相对误差的大小，来验证IncPR的正确性.在比较IncPR与Bahmani的增量算法的正确性时，分别增加不同数量的边比较2种算法的误差，实验表明2种算法具有相同量级的精度水平.在比较IncPR与BasicPR的正确性时，考虑在真实的数据集上，仅增加边和增加点和边2种情况下算法的正确性.此外，通过多组不同的实验，验证了不同的图数据变化量、不同的初始结果精度对IncPR结果精度的影响.

如图6所示，IncPR在结果精度上表现良好.当增量规模较小时(小于1%)，IncPR和BasicPR的结果的误差接近，随着增加节点的比例的增大，IncPR与BasicPR的误差的比在逐渐减小，这意味着IncPR在增加的点较多的情况下(5%和10%)得到比BasicPR更高的结果精度.最优情况下，IncPR的误差比BasicPR减小接近20%.

图7反映了增加不同比例的边(占原图的0.01%到10%)的情况下，IncPR与BasicPR得到的结果误差的比值.边增加的情况下2种算法的误差总体接近，仅有个别图得到了最好情况下接近10%的精度提升.另一组增加不同数量的边的实验结果(如图8所示)，也同样验证了IncPR得到与BasicPR的结果精度在相同量级的结论.

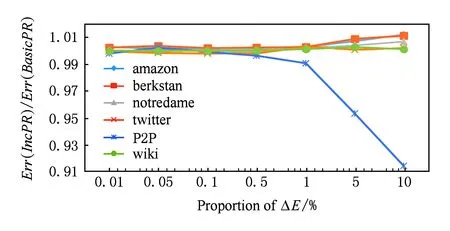
Fig. 7　Comparison of Err(Alg) with different proportion of ΔE.图7　增加不同比例的边的误差比较

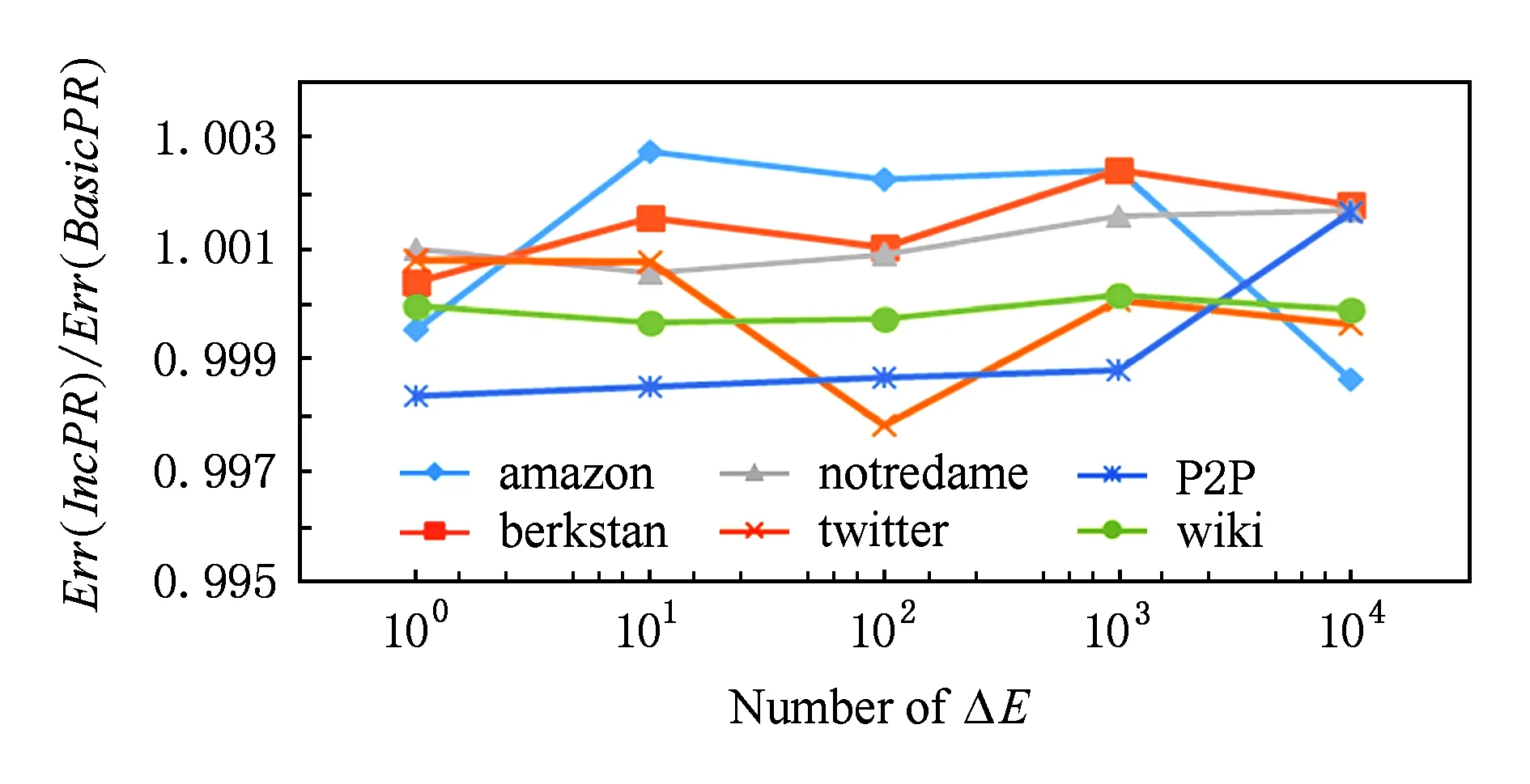
Fig. 8　Comparison of Err(Alg) with different number of ΔE.图8　增加不同数量的边的误差比较

对于IncPR比BasicPR获得的精度提升，一种合理的解释是图的变化一定程度地影响了其拓扑结构，BasicPR的结果精度受图的变化的影响而略有上升，而IncPR采用增量的更新方法，避免了由图的变化而引入更大的误差，从而得到了更好的结果精度.图9所反映的随着节点的增加BasicPR的误差上升，一定程度支持了这种解释.

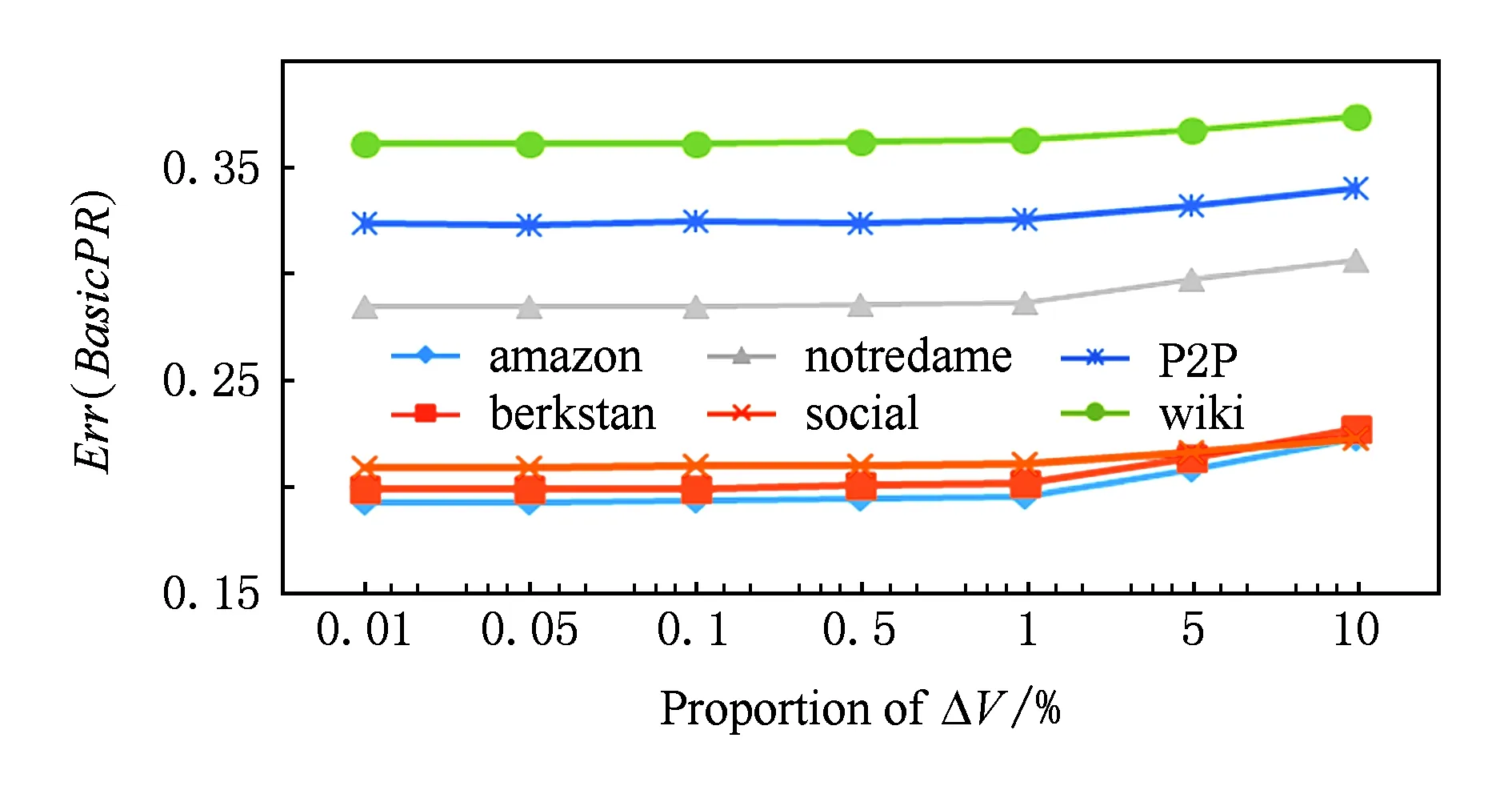
Fig. 9　Err(BasicPR) with different proportion of ΔV.图9　增加不同比例的节点的BasicPR的结果误差

此外，IncPR的一个有价值的特点是，其可以通过重用误差较小的数据获得精度较高的计算结果.这意味着如果以较大的计算代价计算出高精度的PageRank结果，再使用IncPR处理变化后的新图，就可以利用较低的成本获得新的高精度结果，相当于将蒙特卡罗方法适于处理增量和适于并行化的特点与其他的计算代价大但结果精度高的PageRank算法结合了起来，可以充分发挥二者各自的优势.

图10和图11反映了当以PI计算得到的PageRank向量作为初始结果时，增加固定比例的节点和边的情况下分别得到的IncPR的结果误差与BasicPR的误差的比.显然地，当图的变化量较小时(不超过1%)，IncPR得到的结果精度显著优于BasicPR，IncPR得到的结果精度接近PI算法，当增量较大时(5%，10%)，最差情况IncPR的误差也不到BasicPR的一半.

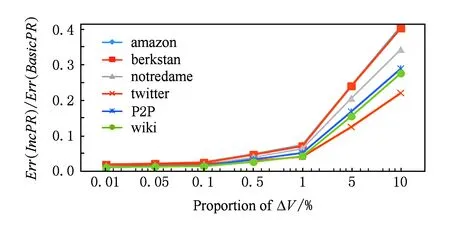
Fig. 10　Comparison of Err(Alg) with different proportion of ΔV (IncPR Starts from PI).图10　增加不同比例的节点误差比较(以PI结果作为初始值)

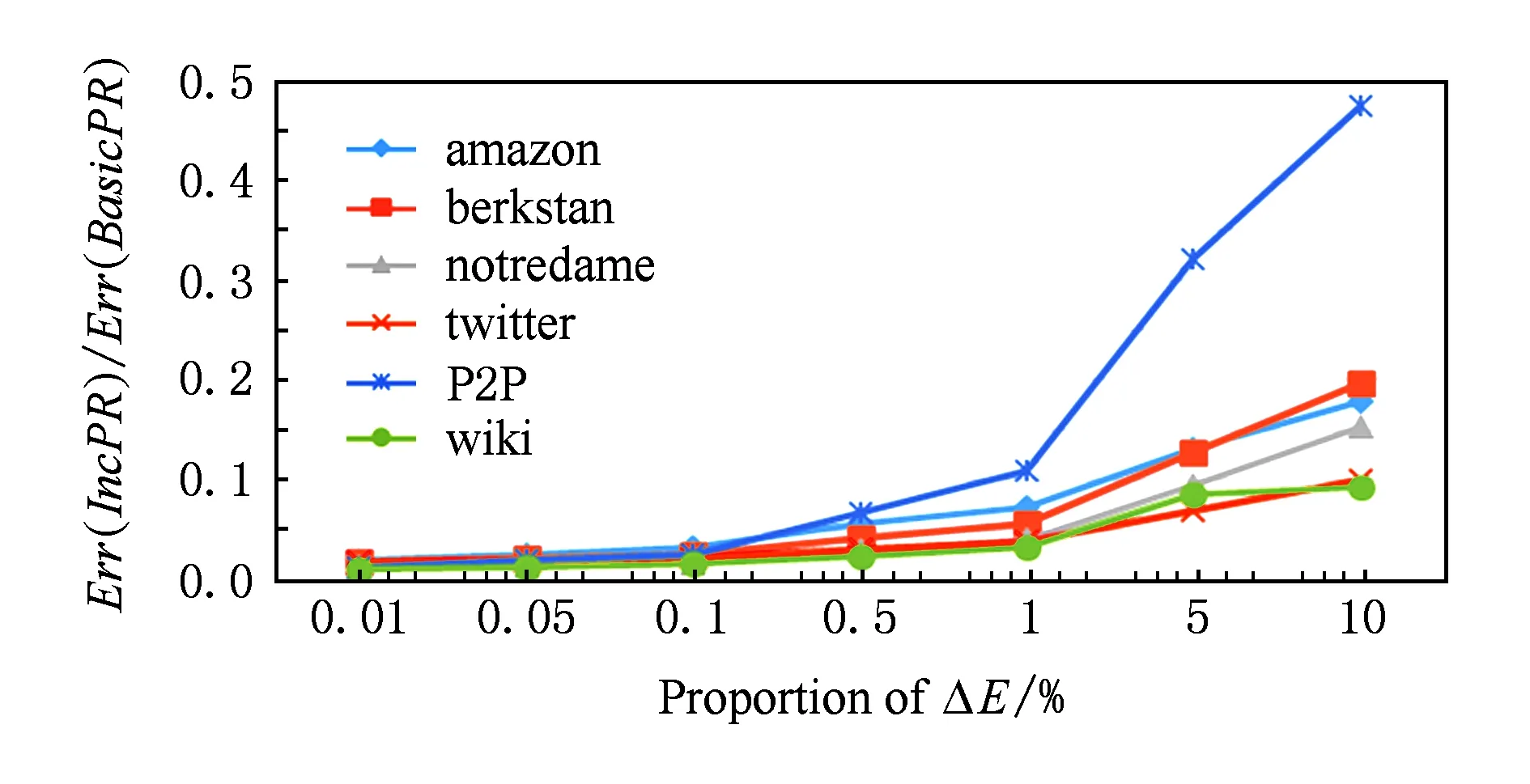
Fig. 11　Comparison of Err(Alg) with different proportion of ΔE (IncPR Starts from PI).图11　增加不同比例的边的误差比较(以PI结果作为初始值)

由于篇幅所限，本文没有给出IncPR与Bahmani的增量算法的正确性比较的数据，2种算法的结果误差值相近.

5.5计算量对比

本文通过多组真实数据集上不同场景的实验，分别比较了IncPR与Bahmani的增量算法及IncPR与BasicPR的计算量的大小，作为评价算法计算效率的标准.

首先对IncPR与Bahmani的增量算法的计算量进行了对比实验，实验结果如表2所示.实验中令增加的边数n分别为50,100和150，由于Bahmani的增量算法每增加一条边就更新结果，因此，实验中统计执行n次Bahmani的增量算法累积的计算量.实验结果均表明IncPR的计算量明显优于Bahmani的增量算法，实验结果验证了IncPR的时间复杂度优于Bahmani的增量算法.虽然与Bahmani的增量算法的对比实验中使用的n较小，但由理论分析可知，IncPR的计算量与n的大小呈线性关系，而Bahmani的增量算法的计算量与节点总数|V|的lnn倍呈线性关系，网络数据中增量的比例占原数据比例较小，n≪|V|.因此在n较大的情况下应该会得到类似的结果.

Table 2　Performance Comparison of Bahmani’s and IncPR表2　Bahmani增量算法与IncPR计算量比较　K

进而，本文分别在不同的数据变化量、初始结果精度等多种条件下进行实验，比较IncPR与BasicPR计算PageRank值的计算量大小，得到算法计算量的统计，作为评价算法计算效率的标准.

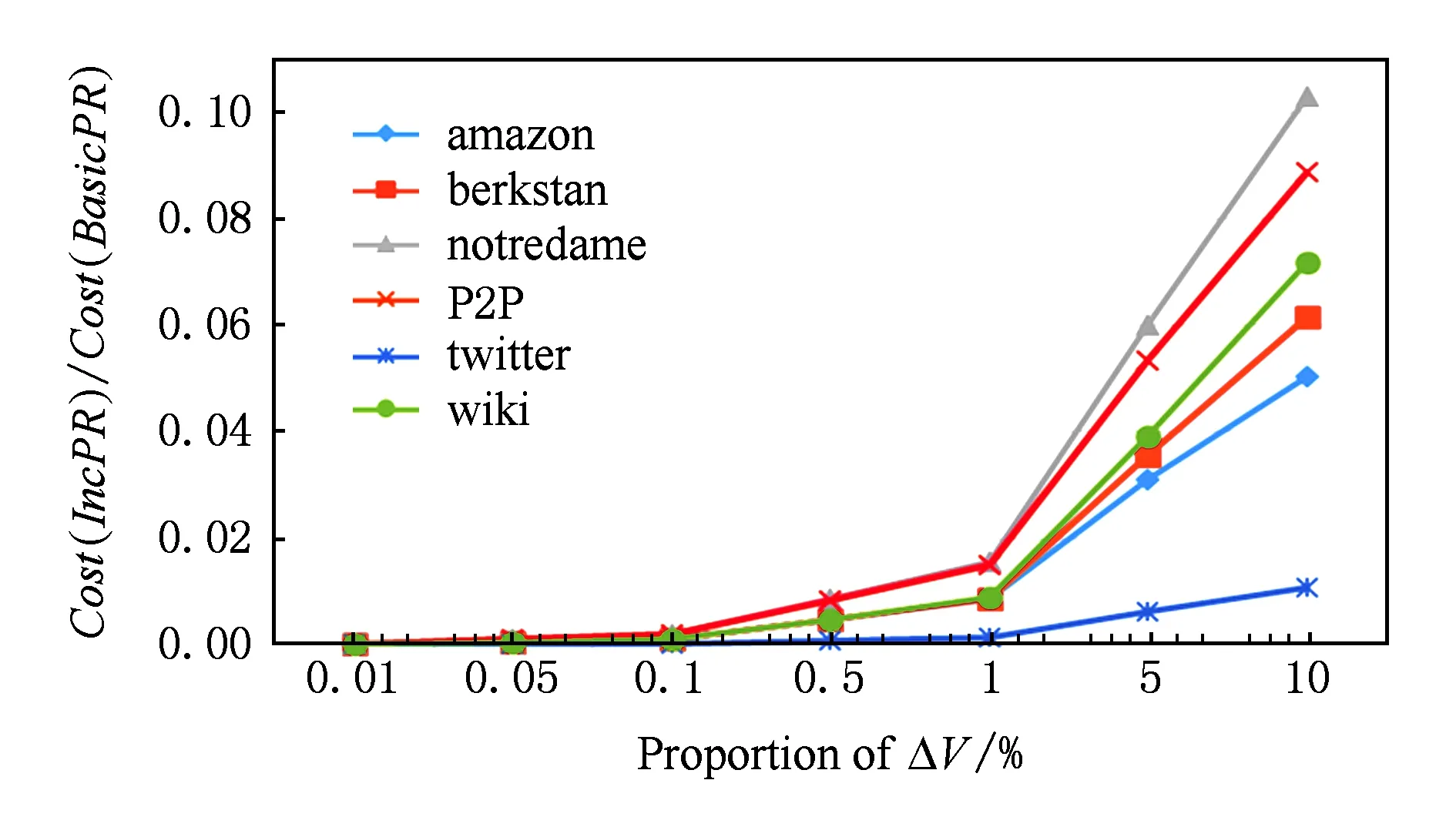
Fig. 12　Comparison of Cost(Alg) with different proportion of ΔV.图12　增加不同比例节点的计算量比较

图12与图13分别反映了增加固定比例的节点和边的情况下，IncPR与BasicPR的计算量的比值.2组实验数据都表现出相同的规律，IncPR的计算量明显小于BasicPR.当图的变化量不超过0.01%时，IncPR的计算量最大仅为BasicPR的0.09%，当图的变化量达到10%时，IncPR的计算量最大仅相当于BasicPR的20%.实验结果表明IncPR能有效地降低PageRank计算的计算量，提高计算效率.

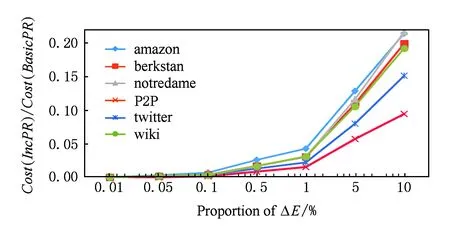
Fig. 13　Comparison of Cost(Alg) with different proportion of ΔE.图13　增加不同比例边的计算量比较

图14反映了增加固定数量的边的情况下，IncPR的计算量的变化趋势，不同数据集上的多组实验反映出相似的规律，即计算量和边的变化量基本符合线性正比例关系，与理论分析得到的算法的时间复杂度大致相符.

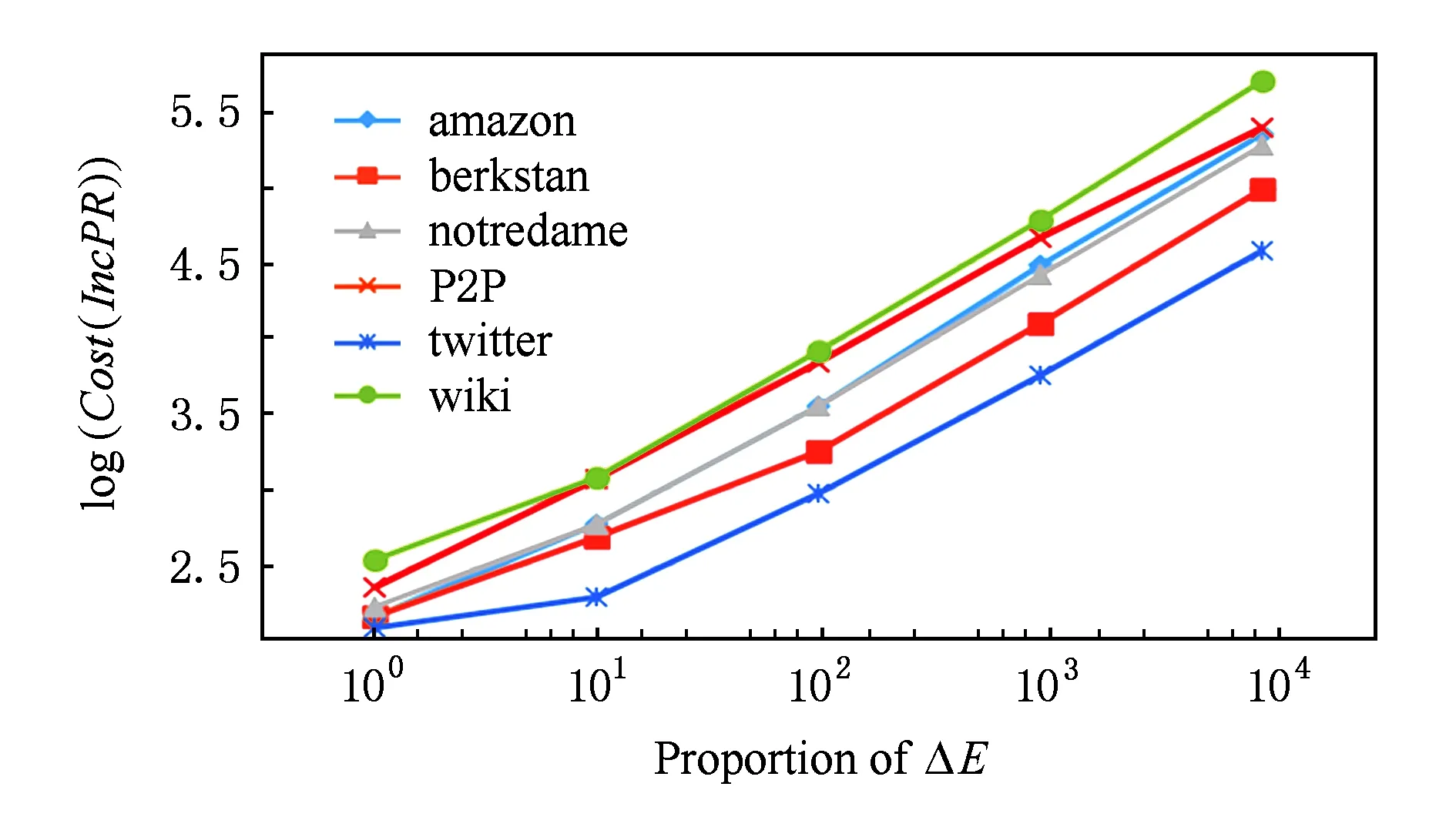
Fig. 14　Relationship of Cost(IncPR) and the number of ΔE.图14　增加边的数量与增量算法计算量的关系

6　总　　结

旨在降低频繁变化的海量数据集上反复计算PageRank带来的资源消耗，本文提出了一种基于增量计算思想的并行PageRank算法——IncPR.IncPR在时间复杂度上优于已有的相关算法，且不引入额外的存储开销.理论分析及基于真实图数据的大量分布式计算实验均验证了IncPR的正确性和计算效率，在保证结果精度的前提下，较之于已有的增量PageRank算法和非增量的PageRank算法，IncPR能够显著地降低计算量.此外，IncPR的设计思想也可以用于改进基于蒙特卡罗模拟技术的其他算法(如个性化PageRank、单源最短路径算法等)，这也将有利于降低此类应用问题的计算成本.

[1]ChinaComputerFederationExpertCommitteeofBigData.WhitePaperonBigDataandIndustryDevelopmentofChina2013[M//OL].Beijing:ChinaComputerFederation, 2013.[2016-03-20].http://www.ccf.org.cn//sites//ccf//ccfziliao.jsp?contentId=2774793649105 (inChinese)

(中国计算机学会大数据专家委员会. 中国大数据与产业发展白皮书2013[M//OL]. 北京: 中国计算机学会, 2013. [2016-03-20].http://www.ccf.org.cn//sites//ccf//ccfziliao.jsp?contentId=2774793649105)

[2]GoogleInc.Googleinsidesearch-google[EB//OL].[2016-03-20].https://www.google.com//intl//ta//insidesearch//howsearchworks//thestory//index.html

[3]KunderM.ThesizeoftheworldwideWeb:EstimatedsizeofGoogle’sindex[EB//OL].[2016-03-20].http://www.worldwidewebsize.com//

[4]WorldWideWebFoundation.Internetlivestats[EB//OL].[2016-03-20].http://www.internetlivestats.com//

[5]PageL,BrinS,MotwaniR,etal.ThePageRankcitationranking:BringingordertotheWeb, 422[R].Stanford,CA:StanfordInfoLab, 1999

[6]DeanJ,GhemawatS.MapReduce:Simplifieddataprocessingonlargeclusters[J].CommunicationsoftheACM, 2008, 51(1): 107-113

[7]ZahariaM,ChowdhuryM,FranklinMJ,etal.Spark:Clustercomputingwithworkingsets[C] //Procofthe2ndUSENIXWorkshoponHotTopicsinCloudComputing(HotCloud).Berkeley,CA:USENIXAssociation, 2010: 10-10

[8]MalewiczG,AusternMH,BikAJC,etal.Pregel:Asystemforlarge-scalegraphprocessing[C] //Procofthe2010ACMSIGMODIntConfonManagementofData.NewYork:ACM, 2010: 135-146

[9]GleichD,ZhukovL,BerkhinP.FastparallelPageRank:Alinearsystemapproach, 38[R].Berkeley,CA:Yahoo!Research, 2004

[10]BahmaniB,ChakrabartiK,XinD.Fastpersonalizedpagerankonmapreduce[C] //Procofthe2011ACMSIGMODIntConfonManagementofData.NewYork:ACM, 2011: 973-984

[11]SarmaAD,MollaAR,PanduranganG,etal.Fastdistributedpagerankcomputation[J].TheoreticalComputerScience, 2015, 561 (PartB): 113-121

[12]AvrachenkovK,LitvakN,NemirovskyD,etal.MonteCarlomethodsinPageRankcomputation:Whenoneiterationissufficient[J].SIAMJournalonNumericalAnalysis, 2007, 45(2): 890-904

[13]ApacheSoftwareFoundation.ApacheHama[EB//OL].[2016-03-20].https://hama.apache.org//

[14]OhsakaN,MaeharaT,KawarabayashiK.EfficientPageRanktrackinginevolvingnetworks[C] //Procofthe21stACMSIGKDDIntConfonKnowledgeDiscoveryandDataMining.NewYork:ACM, 2015: 875-884

[15]LangvilleAN,MeyerCD.Deeperinsidepagerank[J].InternetMathematics, 2004, 1(3): 335-380

[16]SarmaAD,GollapudiS,PanigrahyR.EstimatingPageRankongraphstreams[J].JournaloftheACM, 2011, 58(3): 1165-1182

[17]SarlósT,BenczúrAA,CsalogányK,etal.ToRandomizeornottorandomize:Spaceoptimalsummariesforhyperlinkanalysis[C] //Procofthe15thIntConfonWorldWideWeb.NewYork:ACM, 2006: 297-306

[18]BahmaniB,ChowdhuryA,GoelA.Fastincrementalandpersonalizedpagerank[J].ProceedingsoftheVLDBEndowment, 2010, 4(3): 173-184

[19]KamvarSD,HaveliwalaTH,ManningCD,etal.ExtrapolationmethodsforacceleratingPageRankcomputations[C] //Procofthe12thIntConfonWorldWideWeb.NewYork:ACM, 2003: 261-270

[20]KamvarS,HaveliwalaT,ManningC,etal.ExploitingtheblockstructureoftheWebforcomputingpagerank, 579[R].Stanford,CA:StanfordInfoLab, 2003

[21]LangvilleA,MeyerC.UpdatingPageRankusingthegroupinverseandstochasticcomplementation,CRSC-TR02-32[R].Raleigh:MathematicsDepartment,NorthCarolinaStateUniversity, 2002

[22]LangvilleAN,MeyerCD.Updatingpagerankwithiterativeaggregation[C] //Procofthe13thIntWorldWideWebConfonAlternateTrackPapers&Posters.NewYork:ACM, 2004: 392-393

[23]DesikanP,PathakN,SrivastavaJ,etal.IncrementalPageRankcomputationonevolvinggraphs[C] //SpecialInterestTracksandPostersofthe14thIntConfonWorldWideWeb.NewYork:ACM, 2005: 1094-1095

[24]LofgrenP.OnthecomplexityoftheMonteCarlomethodforincrementalPageRank[J].InformationProcessingLetters, 2014, 114(3): 104-106

[25]TongH,PapadimitriouS,PhilipSY,etal.Proximitytrackingontime-evolvingbipartitegraphs[C] //Procofthe8thSIAMIntConfonDataMining.Philadelphia:SocietyforIndustrialandAppliedMathematicsPublications, 2008: 704-715

[26]McsherryF.AuniformapproachtoacceleratedPageRankcomputation[C] //Procofthe14thIntConfonWorldWideWeb.NewYork:ACM, 2005: 575-582

[27]SeoS,YoonEJ,KimJ,etal.Hama:Anefficientmatrixcomputationwiththemapreduceframework[C] //Procofthe2ndIEEEIntConfonCloudComputingTechnologyandScience,CloudCom.Piscataway,NJ:IEEE, 2010: 721-726

[28]JureLeskovec.Stanfordlargenetworkdatasetcollection[EB//OL].[2016-03-20].http://snap.stanford.edu//data//index.html

JiangShuangshuang,bornin1990.Master.Hermainresearchinterestsincludedistributedcomputing,incrementalcomputinganddatamining.

LiaoQun,bornin1987.PhDcandidate.Hismainresearchinterestsincludedistributedcomputing,taskschedulinganddatamining.

YangYulu,bornin1961.ProfessorandPhDsupervisorinNankaiUniversity.Hismainresearchinterestsincludeinterconnectionnetwork,parallelanddistributedprocessing.

LiTao,bornin1977.PhDandassociateprofessorinNankaiUniversity.MemberoftheACMandtheIEEEComputerSociety,SeniormemberofChinaComputerFederation.Hismainresearchinterestsincludeparallelanddistributedprocessing,high-performancecomputingandnetworkinformationmining.

IncPR:AnIncrementalParallelPageRankAlgorithm

JiangShuangshuang,LiaoQun,YangYulu,andLiTao

(College of Computer and Control Engineering, Nankai University, Tianjin 300350)

PageRankalgorithmplaysanimportantroleinvariousareassuchasinformationretrievalandsocialnetworkanalysis.ThecontinuouslyincreasingsizeofnetworksandthetimelinessrequirementsmakeitbringenormouscomputationaloverheadtorepeatcalculatingPageRankforamassiveandevolvingnetwork.Therefore,IncPR,aPageRankalgorithmbasedontheideaofincrementalcomputationmodelisproposed.IncPRreusesexistingresultsfrompreviouscomputationandmodifiesPageRankvaluesaccordingtothechangedpartofdatasetsaccumulativelyviaanextendedMonteCarlomethod,whichcaneffectivelyavoidreduplicatedcomputationandimprovetheperformanceofPageRankcomputingwithnoadditionalstorageoverhead.TheoreticalanalysisshowsthatthecomputationalcomplexityofIncPRprocessinganevolvingnetworkwithmnodesandnedgeschangedisO((cm+n)Rc2),wherecistheresetprobabilityandRisthenumberofrandomwalksstartingfromeachnode.ThecomputationalcomplexityofIncPRislowerthanotherexistingrelatedalgorithms.Ourevaluationswithtypicalreal-worldgraphsuponaHamaclusteralsodemonstratethatIncPRobtainsPageRankvalueswithequal(orevenhigher)accuracyasthebaselineMonteCarloPageRankalgorithmandreducestheamountofcomputationsignificantly.Inexperimentswith0.01%datachanged,IncPRreducesover99.9%amountofcomputation.

PageRank;Webmining;incrementalcomputing;MonteCarloalgorithm;parallelanddistributedprocessing

2016-03-21；

2016-05-25

TP391