社交网络中多渠道影响最大化方法
李小康 张 茜 孙 昊 孙广中
(安徽省高性能计算重点实验室(中国科学技术大学计算机学院) 合肥 230026)
社交网络中多渠道影响最大化方法
李小康张茜孙昊孙广中
(安徽省高性能计算重点实验室(中国科学技术大学计算机学院)合肥230026)
(国防科学技术大学高性能计算协同创新中心长沙410073)
(lxk727@mail.ustc.edu.cn)
社交网络因为其流行性,近些年得到学术界的广泛关注,社交网络影响最大化是社交网络领域中最流行的问题之一.经典的影响最大化问题是从网络中选取k个初始用户,作为种子用户,让其在网络中传播影响,使得最终受影响的用户数最大化.以往的绝大部分工作针对于单个网络的传播,真实情况下信息是借助多个网络传播的.考虑到信息在多个网络中的传播,提出社交网络中多渠道影响最大化问题,从多个网络中选取k个种子用户,让其同时在多个网络中传播影响,使最终受种子用户影响的用户量最大化.将该问题规约为社交网络影响最大化问题,证明其在独立级联模型下是NP难的.根据问题的特性,提出3种有效的近似解决方法,并在4个真实的社交网络数据中进行实验.实验表明3种的方法能够有效地解决多渠道下的影响力最大化问题.
社交网络;影响最大化;多渠道;NP难;近似方法
近些年来,随着Facebook和微博等社交网络的流行,越来越多的用户喜欢在社交网络中分享自己的观点和其他信息,使得网络影响力传播的研究成为社交网络分析的热点.
通常情况下,用户在网络中有且仅有2种状态:激活和未激活状态,激活表示用户受到某观点的影响,未激活表示未受到影响.为了更好地描述信息或者观点在网络中的传播,Goldenberg等人[1]提出独立级联(independentcascade,IC)模型,IC模型中,用户以一定的概率影响其邻居结点;Granovertter[2]认为用户有一定的坚持度,如果其邻居的激活概率之和大于这个坚持度,则激活该用户,他们提出线性阈值(linearthreshold,LT)模型.IC和LT虽然得到广泛的关注,但是真实世界的影响传播是非常复杂的,一些工作提出基于负面观点的独立级联模型[3]、带有时间限制的独立级联模型[4]和多实体竞争和协作的独立级联模型[5-6]等.
Kempe等人[7]形式化影响最大化问题,并且证明该问题是NP难的.他们提出贪心方法解决该问题,贪心方法被证明具有1-1e的最优保证.贪心方法迭代地选取最具影响增量(种子集合加入该结点带来的影响增量)的结点,每次的选取都会计算所有结点的影响增量,这样的策略是非常低效的.一些工作对经典的方法做改进,效率有一定提升[8-9],但是很难扩展到很大的网络中.一些学者提出一些启发式的方法[10-13],这些方法在效率上有很大提升,实验的效果表现很好,但是缺少理论保证.最近有些学者提出一些接近线性的解决方法,而且这些方法具有最优的理论保证[14-16].
影响最大化问题最近得到广泛的研究,考虑社交网络中的真实场景,一些学者提出影响最大化问题的一些变型,他们提出个性化的影响最大化[17]、基于主题的(在线)影响最大化[18-20]、基于特定用户的在线影响最大化[21-22]、基于位置的在线影响最大化[23]、基于信息覆盖的影响最大化[24]、一定预算下的影响最大化问题[25],Nguyen等人[26-27]和Zhan等人[28]将影响最大化问题引入到多重网络.
上述工作中影响力的传播绝大部分是基于单个网络,而现实世界中个体之间的传播网络复杂很多,对于同一信息我们会同时借助多个不同的网络进行传播,如图1所示.最典型的应用场景是校园生活,比如学校举办一场报告会,我们选择一小部分比较有影响力的学生,让其在朋友同学之间进行宣传,目标是使来听报告的学生数最大化.学生间宣传途径并非单一的,既可以采用传统线下方式口头宣传,也可以借助微博、微信、人人网等多种社交网络传播影响.
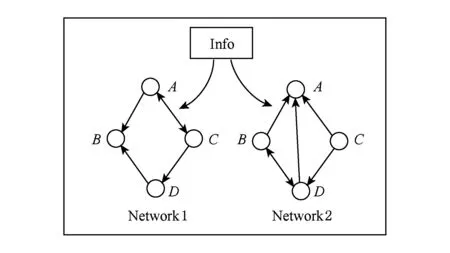
Fig. 1 Process of information propagation.图1 信息传播过程
虽然Nguyen等人[26-27]提出了多重网络影响最大化问题,但是他们问题的模型依赖性很强,只适用于线性阈值模型.我们将问题扩展到更宽泛的影响传播模型,提出了多渠道的影响最大化问题,并形式化定义该问题.我们证明该问题是NP难的,根据该问题的特性,提出3种有效的近似解决方案.真实网络上的实验表明我们提出方法的有效性.本文的贡献如下:
1) 提出多渠道的影响最大化问题,对该问题进行数学化的描述.该问题是根据真实的场景抽象,具有一定的价值.
2) 证明多渠道的影响最大化在独立级联模型下是NP难问题.将该问题归纳为基本的影响最大化问题,证明其是NP难的.
3) 针对该问题,本文提出3种近似的解决方案.通过分析问题的具体特性,参照基本影响最大化的算法,我们提出3种近似的解决方法——贪心方法、基于结点度的方法和基于反向可达集的方法.实验结果表明我们提出方法的有效性.
多渠道影响最大化问题跟多网络相关的问题[26-28]具有一个共同点,都是针对于多个网络,但是具有很大的不同点:1)以往的问题只是针对于改进的线性阈值模型,而我们的问题主要侧重于独立级联模型,而且能够适用于目前绝大部分影响传播模型;2)以往的问题中,多网络的结点集合是不相同的,而我们的问题是针对于特定用户集的,多个网络的结点集合是相同的;3)以往的问题中,结点在多个网络上的传播是交叉的,我们的问题侧重于多渠道之间并行传播影响,结点在多个网络的传播过程是不交叉的.
1 相关工作
随着社交网络的兴起和发展,影响最大化问题得到人们的广泛关注.影响最大化是从网络中选取k个种子结点,让其按照一定的传播模型,在网络中传播影响,最终使受影响的个体最大化.Kempe等人[7]用数学符号形式化该问题,证明该问题在独立级联模型下是NP难的,并提出具有1-1e最优的贪心方法,他们还证明影响力函数具有非负、单调递增和子模特性(sub-modular).因为影响最大化在社交网络中的重要性,近些年来大量的工作改进该问题.我们将这些工作划分为3类:基本方法的改进、传播模型的改进及基本问题的改进.
1.1基本方法的改进
贪心方法每次选取最具影响力结点时,需要计算每个结点的影响增量,独立级联模型下为了获取比较精确的结果,种子结合影响力的计算需要有数万次蒙特卡罗的模拟,导致其效率非常低,很难扩展到较大的社交网络中.在一个中等的社交网络(大概1.5万个结点)中,利用贪心方法选取50个种子结点,在目前大众配置的机器上,需要花费数天的时间,低效率严重限制贪心方法的使用.Leskovec等人[8]利用影响力函数的子模特性,使用优先队列存储结点的影响增量,大幅度地减少种子结点选取过程中影响增量的计算,提出CELF方法,实验表明CELF比起贪心方法大概有700倍的效率提升.Goyal等人[9]提出针对CELF方法的改进版本CELF++,CELF++在上次迭代计算中保存一定的计算结果,减少在下次迭代过程中的计算,实验表明比起CELF方法,CELF++在效率上有大概2倍的提升.
尽管CELF++比起贪心方法已经有很大的提升,仍然很难扩展到很大规模的社交网络中.Chen等人[10]提出一些启发式的方法,比如基于度的方法、基于路径的方法[11-12],这些方法在效率上有很大幅度的提升,而且实验表明他们选择种子集带来的影响力接近贪心方法选取达到的影响力,但是他们有一个明显的缺点:方法达到的影响力没有理论保证.Wang等人[13]提出了基于数据重建的方法,该方法从一个全新的角度解决问题,实验表明他们效果几乎逼近贪心方法的,但是仍然没有理论的保证.
Borgs等人[14]提出一个具有理论保证的接近线性时间的方法RIS.RIS分2部分:结点反向可达集(RRS)和种子结点选择过程,RIS的主要贡献是舍弃用蒙特卡罗模拟计算结点的影响力,而是用结点的反向可达集模拟结点的影响力.Tang等人[15-16]证明了结点反向可达集的数量,提出2步法TIM和TIM+方法,他们还对种子结点选择过程进行优化,提出基于边缘的方法IMM,TIM和IMM的贡献是在保证影响力具有理论保证的情况下,确定反向可达集的具体数量.实验表明IMM的效率已经超过启发式方法,比如IRIE[12].TIMTIM+和IMM方法的时间复杂度接近线性,具有一定的理论保证,而且适用于独立级联、线性阈值和更广泛的模型.
1.2传播模型的改进
独立级联和线性阈值是2个最广泛的影响传播模型.独立级联有2个变型:权重级联(weightcascade,WC)和多价模型(multivalentmodel),权重级联模型中,每条边的激活概率被设置为被指向结点入度的倒数;多价模型是预先设置一个传播概率集合,从该集合中随机选取一个值作为该条边的传播概率,改进的模型广泛应用于文献[10-13]中.
一些学者考虑到影响传播过程中的具体细节,对基本模型做了扩展.1)考虑到影响传播过程中负面观点的出现,提出负面独立级联(independentcascadenegative,IC-N)模型[3].IC-N中结点有3个状态:正面激活、未激活和负面激活.而且引入参数质量因子q,如果结点被负面结点激活,则保持负面激活状态,如果被正面结点激活,则该结点以概率q保持正面激活状态,以1-q概率变成负面激活状态;2)考虑到影响的传播存在竞争关系,提出竞争线性阈值模型(competitivelinearthreshold,CLT)[5].CLT中每条边有2个激活概率,分别表示正面激活概率和负面激活概率;3)考虑到结点之间的影响具有时限性,提出时限性独立级联模型(independentcascademodelwithmeetingevents,IC-M)[4].IC-M中,每个结点激活其邻居结点之前,以一定的概率检测该条边链接是否过期,如果未过期,则执行激活过程,否则认为其结点不能激活该邻居结点;4)考虑到多个实体在网络中传播影响时,会存在竞争或者互补的关系,提出比较性独立级联模型(comparativeindependentcascademodel,Com-IC)[6].Com-IC包括2个主要元素:边阶的信息传播(edge-levelinfor-mationpropagation)和顶点阶自动化(node-levelautomation),这2个元素使最终的采纳决策(影响)依赖于全局采纳概率(globaladoptionprobability).
1.3基本问题的改进
基本的影响最大化问题是从网络中选取k个结点,使受影响的用户最大化,一些学者考虑到现实网络的具体情况,提出影响最大化的各种变型.Guo等人[17]提出个性化的影响最大化,对于给定的结点,求对该结点最具影响力的k个结点;一些工作考虑到用户兴趣,提出基于主题兴趣的在线影响最大化问题[18-20],对于给定的用户行为对兴趣的影响,求种子结合,使得影响的用户量最大化,该问题的贡献是对于给定的用户行为对兴趣的影响,求得用户间的影响概率;另外一些工作优化特定结点集合影响力,提出基于特定用户的影响最大化问题[21-23],给定特定的用户集,求种子集,使这些用户的影响最大化;Wang等人[24]将激活结点的邻居看作信息结点,提出信息影响最大化问题,考虑到选取种子结点是有代价的,Goyal等人[25]提出了一定预算下的影响最大化问题,对于给定的预算,该问题是从网络中选取少部分结点,使得其在网络中影响的结点数最大化.Nguyen等人[26-27]考虑到影响在多个网络中的传播,提出了改进的线性阈值模型下的多重网络影响最大化问题,Zhan等人[28]提出了多重网络影响最大化的改进版本——异构网络影响最大化问题.
2 先验知识
社交网络可以用图的模型G=(V,E)来抽象,V是图中的结点集合,表示社交网络中的用户集合;E表示图中边的集合,代表网络中用户之间的关系.本节主要介绍社交网络影响最大化的形式化定义及独立级联模型的传播过程.
2.1影响最大化
对于给定的图G=(V,E)和整数k,影响最大化是从图中选取一个大小为k的结点集合S,作为种子集合,让其在网络中传播影响,使得最终的影响力|R(S)|最大,其中R(S)是被种子集合S影响的结点集合,影响最大化问题形式化描述为
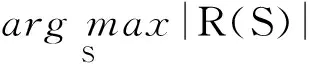
(1)
其中,|S|=k,S⊆V.
Kempe等人[7]证明影响最大化是NP难的.
2.2独立级联模型
独立级联是一种被研究者广泛关注的影响传播模型,该模型中参数pv,w是结点v对其邻居结点w的激活概率,无论是否激活w,v只有一次激活w的机会,而且该过程是独立的,即对w的激活不会受其他结点影响,新激活的结点又会以一定的概率pv,w激活其未激活的邻居结点,直到没有新激活的结点,激活过程结束.激活的结点只有一次机会去激活其邻居结点.一个激活结点激活邻居结点的具体过程如下:
1) 激活的结点放入激活队列中;
2) 激活队列队首出队,以一定的概率激活其邻居结点;若激活,则将邻居结点入队;
3) 重复过程2),直到激活队列为空.
3 问题定义
本节我们对多渠道影响最大化问题给出一个形式化的定义,并证明该问题是NP难的.
对于给定的z个网络G1,G2,…,Gz,Gi=(V,Ei)和整数k,多渠道影响最大化是从z个网络中选取k个结点,作为种子集合,让其分别在z个网络中传播影响,使得z个网络中影响集合并集的元素数最多.多渠道影响最大化可以形式化为
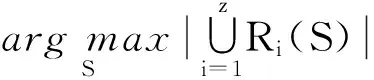
(2)
其中,Ri(S)是种子集S在网络Gi中传播影响时影响的结点集合,|S|=k,S⊆V.
我们的问题针对特定目标的用户,所以不同网络Gi的结点集合是相同的.
定理1. 对于多个社交网络,在独立级联模型下,多渠道影响最大化是NP难问题.
证明. 当网络个数z=1时,多渠道影响最大化问题就转换为经典的影响最大化问题,所以影响最大化问题是多重影响最大化问题的一个特例,Kempe等人[7]证明经典的影响最大化问题是NP难的,因此多重影响最大化在独立级联模型下是NP难问题.
证毕.
4 解决方案
由第3节可知,多渠道影响最大化是NP难的,不存在多项式时间内的最优解.目前的算法存在一个明显的不足——不适用于多渠道下影响力的计算.多渠道影响最大化下,初始用户的影响力计算需要将初始用户在不同网络上的影响集合求并集.根据该问题的特性,我们提出了3种近似的解决方案:贪心方法、基于结点度的方法和基于合成图的方法.
4.1贪心方法
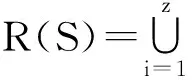
算法1. 贪心方法.
输入:G1,G2,…,Gz,k;
输出:S.
S=∅;
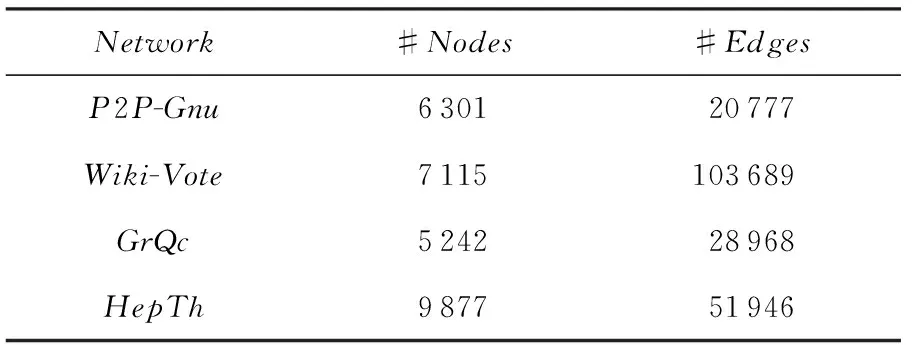
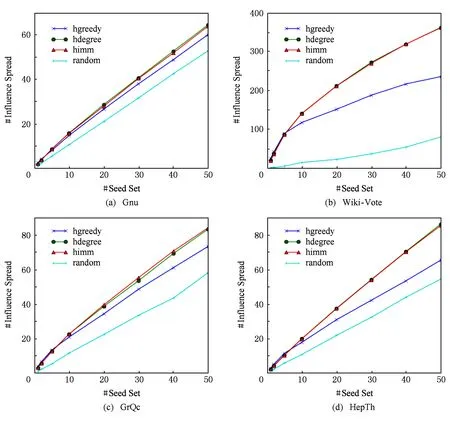
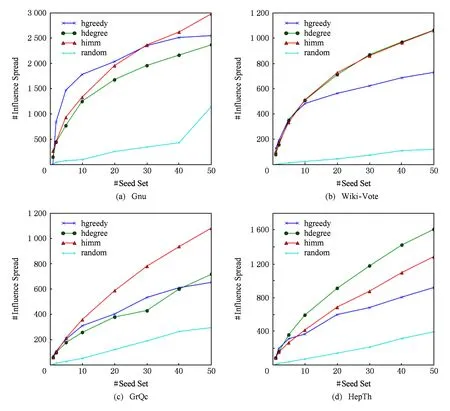
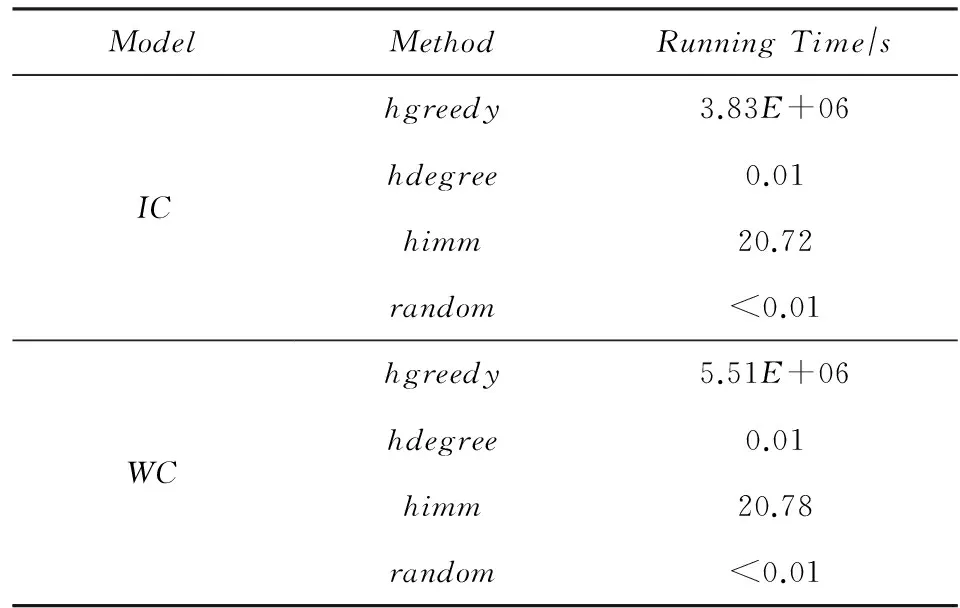
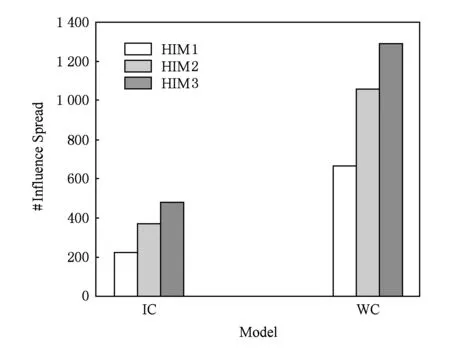
While|S| S=S∪{v}; EndWhile OutputS. 贪心方法每次选取最具影响力结点时,需要计算每个结点的影响增量.独立级联模型下,为了获取比较精确的结果,种子结合影响力的计算需要有数万次蒙特卡罗的模拟,使其效率非常低下,很难扩展到数千个结点数百万条边的网络中.为了满足效率的需求,我们提出一个高效的启发式方法:基于结点度的方法. 4.2基于结点度的方法 一个结点的出度越大,说明它能够影响的邻居越多,一定程度上反映它具有较大的影响力.基于结点度的方法首先计算所有结点在z个网络的出度之和,每次选择具有出度最大的结点,如果一个结点被选作种子结点,其入边邻居就不能再影响它,则其入边邻居的影响力就会减弱,这里我们简单地减1处理,重复上述选择过程直至选出k个种子结点,具体的过程如算法2.由算法2知,基于结点度的方法的时间复杂度为O(k(n+zd)+nz),其中d是结点的平均度数.比起贪心方法,算法2在效率上有大幅度地提升,能够扩展到更大的网络中. 算法2. 基于结点度的方法. 输入:G1,G2,…,Gz,k; 输出:S. S=∅; Foreachv∈V EndFor While|S| S=S∪{v}; Fori=1,2,…,zdo Foreachw∈innodei(v) degree(w)-=1; EndFor EndFor EndWhile OutputS. 在一些影响传播模型下,基于结点度的方法是一种简单有效的方法,但是它有一个基本的假设:结点的出度能够反映结点在网络中的影响力,在经典的独立级联模型下,任意2个结点间的激活概率是相等的,结点的一度(与结点直接相连) 影响力基本可以近似结点的真实影响力,因为结点的二度三度影响力是指数下降的,与一度影响力相比基本可以忽略不计.但是如果结点间的激活概率不相等时,比如权重级联模型(WC),该方法的假设就不再合理,因此基于结点度的方法的适用范围有限.提出一种用于解决多渠道影响最大化问题、效率高、表现好、能适用于多种影响传播模型的方法是非常有必要的. 4.3基于反向可达集的方法 多渠道影响最大化问题计算种子集合S的影响力时,首先计算S在不同网络Gi的影响集合Ri(S),然后对不同的影响集合求并集,得到S在多渠道上的影响力|R(S)|.由于多渠道影响最大化问题影响力的计算需要同时计算不同网络的影响集合,目前流行的方法,比如TIM+[15]和IMM[16],不能直接解决多渠道的影响最大化. 种子集合S的影响力计算过程中,需要同时计算在不同网络中的影响集合,如果一条边(u,v)在z个网络都出现,u对v的激活过程简单认为在一个网络中进行z次,我们将z个网络Gi转换成一个网络G.在G中,结点u对结点v的激活概率pu,v如式(3): (3) 得到网络G后,我们借鉴最新的线性方法[14-16],提出基于反向可达集的方法.基于反向可达集的方法分2步:1)有放回地从结点集合V中随机选择一些结点,在转置图上,进行广度优先搜索(BFS)或者深度优先搜索(DFS)去激活其邻居结点,所有激活的结点组成一个反向可达集(reversereachableset),RR是反向可达集的结合,大小为θ;2)使用最大覆盖方法[29]选择种子集合,首先,选择反向可达集最大覆盖结点加入种子集合S,然后删除包含该结点的反向可达集,重复此过程,直至选取k个种子结点,具体过程如算法3.算法3反向可达集数量θ是受参数ε控制的. 算法3. 基于反向可达集的方法. 输入:G1,G2,…,Gz,k; 输出:S. S=∅;RR=∅; Fori=1,2,…,θdo 从G中随机选择结点u; 计算u的反向集合RRi; RR=RR∪RRi; EndFor Fori=1,2,…,kdo 选择对RR具有最大覆盖的结点u; S=S∪{u}; 从RR中删除包含结点u的集合; EndFor OutputS. 基于反向可达集的方法主要有2个过程:合成图G的生成和从G中选取种子集.如果图中边的影响概率是以散列表的形式存储,则合成图过程的时间复杂度为O(m),从G中选取种子集合过程可以在一个接近现实时间内完成.因此比起贪心的方法,基于反向可达集的方法效率是非常高的. 本节主要介绍实验的基本设置及实验结果与分析. 5.1实验设置 我们使用4个真实的数据集:Gnu网络、Wiki-Vote网络、Hept网络和Phy网络,这些数据广泛应用于很多工作中[9-16].Gnu是Gnutella文件贡献网络,Wiki-Vote是维基百科的投票网络,这2个数据可以从Stanford大学的SNAP项目[30]下载;GrQc和HepTh是文章合作网络,分别来自广义相对论量子宇宙和高能源物理,可以从Stanford大学的SNAP项目下载[30],数据的详细信息如表1所示.为了模拟信息在多渠道的传播,我们将网络数量z设置为2,网络G2和网络G1是在原始网络中随机删除20%的边. Table1 Details of Network on Experiments表1 实验网络的详细信息 本次实验是基于IC模型和WC模型的.IC模型下结点间的影响概率p=0.01;WC模型下,结点u对其邻居结点v的影响力设为结点v的入度的倒数1indegree(v),其中indegree(v)是结点v的入度.为了得到较为准确的影响力,实验中所有影响力的计算,我们使用蒙特卡罗模拟,模拟次数r=20 000,基于反向可达集的方法中的ε=0.1.实验中我们共使用4种方法. 1) 在4.1节提出的贪心方法. 2) 在4.2节提出的基于结点度的方法. 3) 在4.3节提出的基于反向可达集的方法. 4) 随机的方法,从结点集合中随机选取k个种子结点,该方法曾作为对比方法叙述于文献[7,10]中. 实验程序是用C++实现的,运行于Linux服务器上。服务器的CPU配置为Intel®CoreTMi5-4460CPU@ 3.20GHz,内存为8GB. 5.2实验结果与分析 1) 影响力比较. 我们在4个真实的数据集上实验测试种子数量从1~50,将4种方法选取的种子结点在多渠道上传播影响,用蒙特卡罗模拟其影响力,具体的结果如图2、图3所示,图2和图3分别是在IC模型和WC模型下的结果,其中hgreedy,hdegree,himm分别表示我们提出的用于解决多渠道影响最大化的贪心方法、基于结点度的方法和基于反向可达集的方法,random表示随机的方法,分图(a)~(d)分别表示在Gnu,Wiki-Vote,GrQc,HepTh网络的影响力. Fig. 2 Influence spread of different methods on 4 real datasets under IC model.图2 IC模型不同的方法在4个真实数据上得到的影响力 Fig. 3 Influence spread of different methods on 4 real datasets under WC model.图3 WC模型不同的方法在4个真实数据上得到的影响力 由图2和图3可知,随机的方法效果最差,主要是因为它选择种子结点只是随机地选择k个种子结点,并不依赖于网络的拓扑和结点间的影响力.当种子个数比较少时,贪心方法、基于结点度的方法和基于反向可达集的方法表现相当,因为他们都是基于一定的贪心策略选择,这些策略一定程度上能够反映结点的影响力. 由图2可知,基于反向可达集的方法和基于结点度的方法的表现明显高于贪心方法.基于反向可达集的方法是用结点覆盖反向可达集的数量来预估其影响力,每选择一个最大覆盖的结点会删除其覆盖的反向可达集.基于结点度的方法优先选择度大的结点,IC模型下,每条边的激活概率相同,结点的出度基本反映其影响力,而且这2种方法每次的种子结点选择会降低其邻居结点影响力,使得最终的种子结点能够覆盖网络中的较大区域.多渠道下影响力函数并不满足子模特性,贪心地选择种子结点很容易得到局部最优解. 由图3可知,WC模型下基于反向可达集的方法仍然表现很好,主要是该方法不依赖于边的影响概率,适用于绝大部分传播模型.而基于结点度的方法在不同数据网络上的表现差异很大,WC模型下每条边的激活概率不等,结点的出度并不能对应结点的影响力,仍然依靠出度去选种子结点,选出的种子集合不一定能够带来很大的影响力. 2) 效率比较. 为了比较各种方法的效率,我们测试4种方法在HepTh网络上选取50个种子集合所用的时间,我们在IC和WC模型下分别测试,具体的结果如表2所示.由表2可知,随机方法和基于结点度的方法效率是非常高的,前者仅依赖于网络中结点的数量和种子的数量,后者还依赖结点的度,这些量一般是给定的或者是很容易计算.贪心方法在选择种子结点时,需要模拟每个结点加入种子集合后的影响力,而每次模拟需要有数万次的蒙特卡罗的模拟,所以贪心方法效率非常低,基于反向可达集的方法用结点覆盖反向可达集的数量近似模拟结点的影响力,替代蒙特卡罗的模拟,而且每个结点的近似影响力只需要计算一次,因此其效率非常高. Table 2 Running Time Comparison of Different Methods表2 不同方法运行时间对比 3) 网络个数讨论. Fig. 4 Influence spread comparison under different number of networks.图4 不同网络个数下影响力对比 图4展示了在Wiki-Vote网络上,针对多渠道下影响最大化问题中不同网络个数,选取50个种子结点在对应网络个数上的影响力,我们分别测试在2种传播模型:IC模型和WC模型,其中HIM1,HIM2,HIM3分别表示在网络G1、2个网络(G1和G2)和3个网络(G1,G2,G3)上,使用基于反向可达集的方法选取的种子集合在各自不同的网络上产生的影响力.网络G3的获取方式是与网络G1和G2是一样的,从原始网络中随机删除20%的边,实验中我们最多模拟3个网络,因为现实世界中,主流的社交网络个数比较少.由图4可知,随着网络个数的增加,选取同样大小的种子集合,产生的影响力越大,而且影响的增量会有一定的下降,2个网络与1个网络相比,IC模型和WC模型下影响力分别有66.75%和59.24%的提升,3个网络与2个网络相比,IC模型和WC模型下影响力分别有28.14%和21.87%的提升.直观地理解,信息在多个网络中传播影响会比在单个网络中产生的影响大,从侧面说明我们提出问题的合理性. 4) 采样比例讨论与单网络方法对比. 本次实验有2个目标:①比较不同边采样下的影响力;②比较我们提出的方法与对应的单网络方法产生的影响力.我们在Gnu网络上的WC模型下,从原始网络中随机删除20%,30%,50%的边生成相应的网络,使用基于结点度的方法与其对应的单网络影响最大化方法选取50个种子结点,然后计算其影响力.具体结果如图5所示,其中WC2,WC3,WC5分别表示网络是从原始网络中随机删除20%,30%,50%的边,hdegree,degree分别表示我们提出的基于结点度的方法与其对应的单网络的方法(用基于结点度的方法从其中一个网络中选取种子集合). Fig. 5 Edge sample ratio discuss and comparison with method for single network.图5 边采样比例讨论与单网络方法对比 由图5可知,随着网络中边数量的增加,同一种方法选取相同的数量的种子结点,在相应的网络中产生的影响力随之增加,因为网络中边数量越多,种子结点能激活的邻居结点越多,最终受影响的结点数量越多,则产生的影响力越大.不同比例的边采样的情况下,基于结点度的方法选取的种子集合产生的影响力比其对应的单网络方法选取的种子集合产生的影响力大,因为单网络的方法是从其中一个网络中选取种子结点,相当于选取种子结合时只依靠部分信息,选取的种子结点难免产生较差的影响力. 考虑到信息或者观点的传播会借助多个网络,本文提出多渠道影响最大化问题,用数学的方法形式化该问题;通过将多渠道影响最大化问题归纳为基本的影响最大化问题,我们证明多渠道影响最大化是NP难问题;针对该问题的基本特性,我们提出3种近似的解决方法:贪心方法、基于结点度的方法和基于反向可达集的方法;真实网络上的实验结果表明我们提出方法的有效性. 本文提出了多渠道影响的影响最大化问题,接下来的工作会侧重3个方面:1)深入理解问题的性质,找到效率更高的计算影响力的方法;2)寻找用于解决多渠道影响最大化问题效率更高、效果更好的方法;3)针对种子结点在多个网络传播影响的独立性,使用并行的策略优化影响力的计算. [1]GoldenbergJ,LibaiB,MullerE.Talkofthenetwork:Acomplexsystemslookattheunderlyingprocessofword-of-mouth[J].MarketingLetters, 2001, 12(3): 211-223 [2]GranovetterM.Thresholdmodelsofcollectivebehavior[J].AmericanJournalofSociology, 1978, 83(6): 1420-1443 [3]ChenW,CollinsA,CummingsR,etal.Influencemaximizationinsocialnetworkswhennegativeopinionsmayemergeandpropagate[C] //Procofthe11thSIAMIntConfonDataMining(ICDM).Philadelphia,PA:SIAM, 2011: 379-390 [4]ChenW,LuW,ZhangN.Time-criticalinfluencemaximizationinsocialnetworkswithtime-delayeddiffusionprocess[C] //Procofthe26thConfonArtificialIntelligence.PaloAlto,CA:AAAI, 2012 [5]HeX,SongG,ChenW,etal.Influenceblockingmaximizationinsocialnetworksunderthecompetitivelinearthresholdmodel[C] //Procofthe12thSIAMIntConfonDataMining.Philadelphia,PA:SIAM, 2012: 463-474 [6]LuW,ChenW,LakshmananLVS.Fromcompetitiontocomplementarity:Comparativeinfluencediffusionandmaximization[J].VLDBEndowment, 2015, 9(2): 60-71 [7]KempeD,KleinbergJ,Tardosé.Maximizingthespreadofinfluencethroughasocialnetwork[C] //Procofthe9thACMSIGKDDIntConfonKnowledgeDiscoveryandDataMining.NewYork:ACM, 2003: 137-146 [8]LeskovecJ,KrauseA,GuestrinC,etal.Cost-effectiveoutbreakdetectioninnetworks[C] //Procofthe13thACMSIGKDDIntConfonKnowledgeDiscoveryandDataMining.NewYork:ACM, 2007: 420-429 [9]GoyalA,LuW,LakshmananLVS.CELF++:Optimizingthegreedyalgorithmforinfluencemaximizationinsocialnetworks[C] //Procofthe20thIntConfCompaniononWorldWideWeb.NewYork:ACM, 2011: 47-48 [10]ChenW,WangY,YangS.Efficientinfluencemaximizationinsocialnetworks[C] //Procofthe15thACMSIGKDDIntConfonKnowledgeDiscoveryandDataMining.NewYork:ACM, 2009: 199-208 [11]ChenW,WangC,WangY.Scalableinfluencemaximizationforprevalentviralmarketinginlarge-scalesocialnetworks[C] //Procofthe16thACMSIGKDDIntConfonKnowledgeDiscoveryandDataMining.NewYork:ACM, 2010: 1029-1038 [12]JungK,HeoW,ChenW.IRIE:Scalableandrobustinfluencemaximizationinsocialnetworks[C] //Procofthe12thIEEEIntConfDataMining(ICDM).Piscataway,NJ:IEEE, 2012: 918-923 [13]WangZ,WangH,LiuQ,etal.Influentialnodesselection:Adatareconstructionperspective[C] //Procofthe37thIntACMSIGIRConfonResearch&DevelopmentinInformationRetrieval.NewYork:ACM, 2014: 879-882 [14]BorgsC,BrautbarM,ChayesJ,etal.Maximizingsocialinfluenceinnearlyoptimaltime[C] //Procofthe25thAnnualACM-SIAMSymponDiscreteAlgorithms.Philadelphia,PA:SIAM, 2014: 946-957 [15]TangY,XiaoX,ShiY.Influencemaximization:Near-optimaltimecomplexitymeetspracticalefficiency[C] //Procofthe7thACMSIGMODIntConfonManagementofData.NewYork:ACM, 2014: 75-86 [16]TangY,ShiY,XiaoX.Influencemaximizationinnear-lineartime:Amartingaleapproach[C] //Procofthe8thACMSIGMODIntConfonManagementofData.NewYork:ACM, 2015: 1539-1554 [17]GuoJ,ZhangP,ZhouC,etal.Personalizedinfluencemaximizationonsocialnetworks[C] //Procofthe22ndACMIntConfonInformation&KnowledgeManagement.NewYork:ACM, 2013: 199-208 [18]AslayÇ,BarbieriN,BonchiF,etal.Onlinetopic-awareinfluencemaximizationqueries[C//OL]. 2016[2016-03-10].http://www.francescobonchi.com//inflex.pdf [19]ChenS,FanJ,LiG,etal.Onlinetopic-awareinfluencemaximization[J].VLDBEndowment, 2015, 8(6): 666-677 [20]LiY,ZhangD,TanKL.Real-timetargetedinfluencemaximizationforonlineadvertisements[J].VLDBEndowment, 2015, 8(10): 1070-1081 [21]LiFH,LiCT,ShanMK.Labeledinfluencemaximizationinsocialnetworksfortargetmarketing[C] //Procofthe3rdPrivacy,Security,RiskandTrust(PASSAT)andProcofthe3rdIntConfonSocialComputing(SocialCom).Piscataway,NJ:IEEE, 2011: 560-563 [22]LeeJR,ChungCW.Aqueryapproachforinfluencemaximizationonspecificusersinsocialnetworks[J].IEEETransonKnowledgeandDataEngineering, 2015, 27(2): 340-353 [23]LiG,ChenS,FengJ,etal.Efficientlocation-awareinfluencemaximization[C] //Procofthe7thACMSIGMODIntConfonManagementofData.NewYork:ACM, 2014: 87-98 [24]WangZ,ChenE,LiuQ,etal.Maximizingthecoverageofinformationpropagationinsocialnetworks[C] //Procofthe24thIntConfonArtificialIntelligence.PaloAlto,CA:AAAI, 2015: 2104-2110 [25]GoyalA,BonchiF,LakshmananLVS,etal.Onminimizingbudgetandtimeininfluencepropagationoversocialnetworks[J].SocialNetworkAnalysisandMining, 2013, 3(2): 179-192 [26]NguyenDT,DasS,ThaiMT.Influencemaximizationinmultipleonlinesocialnetworks[C] //Procofthe32ndtheGlobalCommunicationsConf(GLOBECOM).Piscataway,NJ:IEEE, 2013: 3060-3065 [27]NguyenDT,ZhangH,DasS,etal.Leastcostinfluenceinmultiplexsocialnetworks:Modelrepresentationandanalysis[C] //Procofthe13thIntConfonDataMining.Piscataway,NJ:IEEE, 2013: 567-576 [28]ZhanQ,ZhangJ,WangS,etal.Influencemaximizationacrosspartiallyalignedheterogenoussocialnetworks[C] //ProcofPacific-AsiaConfonKnowledgeDiscoveryandDataMining.Berlin:Springer, 2015: 58-69 [29]VaziraniVV.ApproximationAlgorithms[M].Berlin:SpringerScience&BusinessMedia, 2013 [30]LeskovecJ,KrevlA.SNAP[EB//OL]. 2016[2016-03-10].http://snap.stanford.edu//data LiXiaokang,bornin1990.MasterfromtheUniversityofScienceandTechnologyofChina.Hismainresearchinterestsincludesocialnetwork,bigdataprocessingandprivacypreserving. ZhangXi,bornin1993.MastercandidateintheUniversityofScienceandTechnologyofChina.Hermainresearchinterestsincludedatamining. SunHao,bornin1994.MastercandidateintheUniversityofScienceandTechnologyofChina.Hismainresearchinterestsincludebigdataanalysis. SunGuangzhong,bornin1978.PhD,associateprofessorintheUniversityofScienceandTechnologyofChina.Hismainresearchinterestincludehighper-formancecomputing,algorithmoptimiza-tionandbigdataanalysis. InfluenceMaximizationAcrossMulti-ChannelsinSocialNetwork LiXiaokang,ZhangXi,SunHao,andSunGuangzhong (Anhui Province Key Laboratory of High Performance Computing (School of Computer Science, University of Science and Technology of China), Hefei 230026) (Collaborative Innovation Center of High Performance Computing, National University of Defense Technology, Changsha 410073) Socialnetworkshavewidelyattractedtheinterestsofresearchersinrecentyearsbecauseoftheirpopularity.Influencemaximizationinsocialnetworkisoneofthemostpopularproblemsofsocialnetworkfields.Influencemaximizationinsocialnetworkisaproblemtopickupkseedusersfromasocialnetwork,targetthemasseedusersandpropagateinfluenceviathenetwork,withthegoalofmaximizingthenumberofusersinfluencedbyseednodes.Themajorityofpreviousworkisbasedonasinglechannel.However,inrealworld,informationispropagatedviamultiplechannels.Thispapertakesinformationspreadinmultiplenetworksintoconsideration,proposesandformulatesinfluencemaximizationproblemacrossmulti-channelsinsocialnetwork.Theproblembecomestopickupkseedusersfrommultiplenetworksandsimultaneouslypropagateinfluenceacrossmultiplenetworks,maximizingthenumberofinfluencedusersbyseedset.WeprovetheproblemisNP-hardunderindependentcascademodelthroughreducingitintoinfluencemaximizationinsocialnetwork.Accordingtothepropertyoftheproblem,weputforwardthreeefficientandeffectiveapproximationmethodsforit.Experimentsshowourproposedmethodsareeffectiveonfourrealsocialnetworks. socialnetwork;influencemaximization;multi-channels;NP-hard;approximationmethods 2016-03-21; 2016-06-03 国家自然科学基金项目(61303047) 孙广中(gzsun@ustc.edu.cn) TP391 ThisworkwassupportedbytheNationalNaturalScienceFoundationofChina(61303047).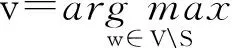
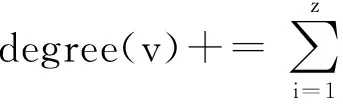
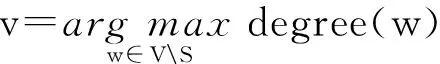
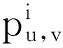
5 实 验

6 结束语





