基于随机栅格的异或区域递增式视觉密码方案
胡 浩 沈 刚 郁 滨 马浩俊夫
(信息工程大学密码工程学院 郑州 450001)
基于随机栅格的异或区域递增式视觉密码方案
胡浩沈刚郁滨马浩俊夫
(信息工程大学密码工程学院郑州450001)
(wjjhh_908@163.com)
针对现有区域递增式视觉密码方案仅局限于或运算,导致秘密图像中白像素无法被正确恢复的问题,给出了基于异或运算的区域递增式视觉密码的定义.通过迭代基于随机栅格的(k,k)单秘密视觉密码方案,利用0是异或{0,1}群中单位元的特性,设计了适用于异或运算的(k,n)单秘密方案的共享份生成算法,并构造了(k,n)区域递增式方案的秘密分享与恢复流程,分享过程中对于原像素s,依据s所在区域的密级,通过随机选取一个授权子集Q对s重新赋值,并利用(k,n)单秘密方案完成像素加密.恢复过程同一般视觉密码方案相同,最后对方案的有效性进行了理论证明.实验结果表明,该方案不仅实现了像素不扩展,且所有共享份叠加时白像素可以完美恢复.
图像秘密共享;视觉密码;密级;区域递增式;随机栅格;异或
视觉密码[1](visualcryptography,VC)是秘密共享技术在数字图像领域的一种应用,继承了秘密共享的特点,同时具有自身独特的秘密恢复简单性,自1994年提出以来便引起了国内外学者的广泛关注[2-8].受当时个人计算机不够普及的制约,共享份多以透明胶片为载体,解密图像则通过直接叠加共享份并利用视觉系统观察平均效果来实现.这种方式的恢复实质上是对共享份进行或(OR)运算,其代数结构为加法半群,由于白像素(0)不存在逆元(1⊗1=1,0⊗1=1),导致白像素无法完美恢复,因而原白色区域在恢复图像中的色彩偏黑,致使图像的对比度低,显示效果不清晰.
随着信息技术的快速发展,具有简单计算机能力的智能终端日益普及,借助手机、PDA等手持设备来恢复秘密比透明胶片等专用设备更加快捷方便.某些通过透明胶片不可能完成的运算,例如异或(XOR)运算在智能终端上执行就变得非常简单,极大地丰富了视觉密码解密运算的实现方式.因此,被赋予新内涵的视觉密码凭借解密简单、信息量大的特点必定具有广阔的应用前景[9-11].
传统视觉密码方案在加密时将整幅图像的内容看作一个整体,解密时也是整体恢复,然而在实际应用中,图像中不同内容反映信息的敏感程度往往不同,区域递增式视觉密码(regionincrementingVC,RIVC)作为视觉密码的一个新研究领域,能够实现对图像内容信息的分级保护.在RIVC中,原图像被划分为多个区域,解密时叠加共享份的数量越多,恢复区域的数量也随之越多.实际应用时可依据图像内容信息的重要程度,将图像划分为多个密级区域,对于高密级区域,需要更多参与者共同完成秘密恢复,可以应用于信息的分级管理、多级访问控制和身份认证等方面[8],有效扩展了视觉密码的应用领域.
Wang[12]结合OR运算,设计了一种基于加密矩阵(encodingmatrix,EM)的(2,n)-ORIVC(OR-basedRIVC),可以实现在n个参与者中分享n-1级密级信息,对于不同区域利用不同加密矩阵完成分享,在秘密恢复时,叠加任意2≤t≤n个共享份可以解密t-1个区域的秘密信息,但参与者人数n仅局限于3,4,5.Shyu等人[13]通过建立关于加密矩阵的线性规划模型,构造了一种像素扩展度最优的(2,n)方案,适用于任意数量的参与者,但模型计算复杂度随着n的增加呈指数级增长,且原图像中的黑白像素在恢复图像中产生了色彩反转.Yang等人[14-16]通过拼接单秘密视觉密码(OR-basedVC,OVC)的加密矩阵,突破了(2,n)结构的限制,构造了2种(k,n)-ORIVC的加密矩阵,通过叠加任意k≤t≤n个共享份可以恢复t-k+1个区域的秘密图像,且克服了恢复图像色彩反转失真的问题.李吉亮等人[17]针对不同区域恢复对比度不相等的问题,设计了2种解密区域对比度相等的构造方案,解决了现有方案与传统黑白二值视觉密码不兼容的问题.上述方案主要依靠构造精简的加密矩阵来降低像素扩展度,各区域的加密本质仍是单秘密方案,利用达到恢复门限值的区域显示、未达到恢复门限值的区域无法显示来实现区域递增式的解密效果.事实上,各区域加密矩阵本质上是单秘密方案加密矩阵的线性组合,因而随着k和n的增加,矩阵规模迅速增加,像素扩展度急剧增大,恢复图像的效果也随之降低.例如,当n分别为3,4,5时,(2,n)方案最小像素扩展分别为4,10,20,恢复区域中的最高对比度对应0.5,0.4,0.35,最低对比度对应0.25,0.1,0.05.
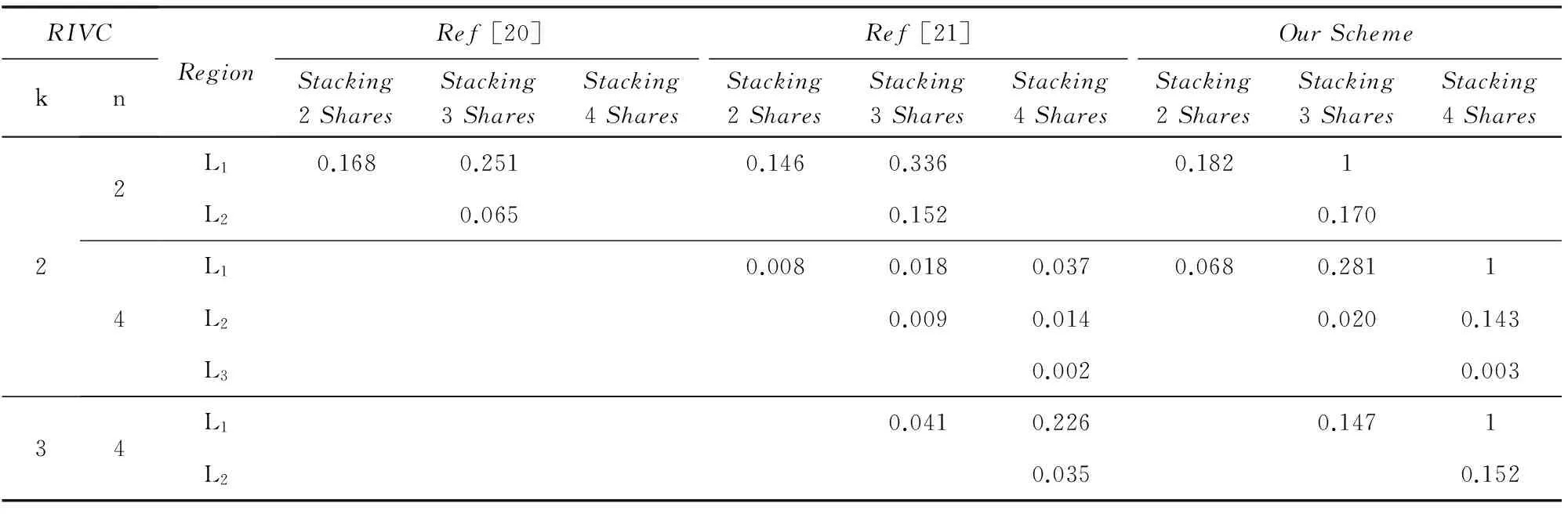
为了解决像素扩展度大的问题,文献[18-19]提出了基于随机栅格(randomgrid,RG)的视觉密码(RG-basedVC,RGVC),共享份是大小与原图像相等的光栅,将它们叠加在一起,利用白黑区域的光通量不同来显示秘密图像.RGVC的优点是分享过程不依赖加密矩阵,仅依靠随机函数来完成秘密分享,因而构造方法丰富.Wang等人[20]给出了基于OR运算的(2,3)区域递增式方案(OR-basedRGRIVC,ORGRIVC)的设计方法,在完成区域逐级解密的前提下,实现了像素不扩展,大幅减小了共享份的存储与传输开销,但仅适用于分享2级秘密信息.Zhong等人[21]在此基础上,设计了(k,n)-ORGRIVC,将存取结构拓展到任意(k,n)结构,显著提高了分享密级的数量,但恢复图像效果不清晰的问题始终没有得到解决.例如,对于(2,3)方案,恢复区域的最高、低对比度分别为0.336,0.146,对于(2,4)方案,分别为0.037,0.002.
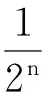
针对上述问题,本文结合XOR运算,设计了一种基于随机栅格的(k,n)区域递增式方案,利用0是异或{0,1}群中单位元的特性(任何元素和0元素XOR运算结果不变),给出了随机栅格的单秘密RGVC的共享份生成算法,在此基础上构造了适合异或运算的RGRIVC的秘密分享与恢复流程.实验结果表明,本方案在实现像素不扩展的前提下,完成了白像素的完美恢复.
1 基本概念
为方便描述,文中所用符号及表达式的含义见表1所示:

Table 1 Some Notations and Their Meanings in This Paper表1 本文所用符号及其含义
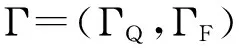
定义2[18].记S(0),S(1)表示秘密图像S中白、黑像素对应的区域,满足S=S(0)∪S(1)且S(0)∩S(1)=∅.另记R[S(0)]和R[S(1)]表示S(0)和S(1)在图像R中的相同位置上的像素组成的集合.对于图像S中位置(x,y)上的像素s,光通量 t(s)=1(0)表示白(黑)像素.对于尺寸X×Y的整幅图像S,平均光通量定义如下:

定义3[19].任意t个共享份Ri1,…,Rit进行XOR运算后,恢复图像Ri1⊕i2⊕…⊕it=Ri1⊕…⊕Rit的对比度定义如下:
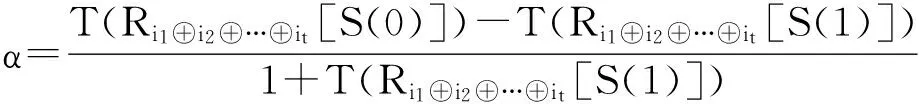
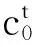
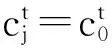
关于上述定义的2点补充说明:
1) 在定义3中,对比度α表示恢复图像的可识别程度,其越大越好.当α=0时,表示从恢复图像中无法得到任何秘密信息,当α=1时,表明恢复图像与原始图像完全一致,实现了完美恢复.
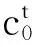
2 (k,n)-RGVC共享份生成算法
单秘密方案是区域递增式方案的实现基础,本节给出基于XOR运算的(k,n)-RGVC的共享份生成算法.基本思想是以(k,k)-RGVC为核心,通过迭代的方法依次加密图像S中的每个像素,共享份生成流程如图1所示,具体步骤如下:
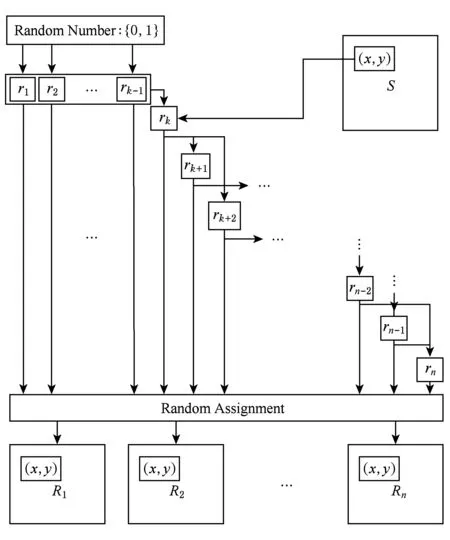
Fig. 1 The shares generation algorithm of RGVC.图1 RGVC的共享份生成算法
算法1.RGVC共享份生成算法.
输入:门限结构(k,n),2≤k≤n,秘密图像S,尺寸大小为X×Y;
输出:共享份Ri,1≤i≤n.
步骤1. 令x=1,x表示正在加密的行号;
步骤2. 令y=1,y表示正在加密的列号;
步骤3. 按行列顺序依次扫描S位置(x,y)上的像素s,则共享份R1,R2,…,Rn对应位置像素R1(x,y),R2(x,y),…,Rn(x,y),由步骤4~8生成;
步骤4. 随机选取一个最小授权集合K={i1,i2,…,ik};
步骤5. 随机生成k-1位{0,1}序列r1,r2,…,rk-1;
步骤6. 令rk=s⊕r1⊕r2⊕…⊕rk-1;
步骤7. 令rk+1,rk+2,…,rn=0;
步骤8. 对r1,r2,…,rn进行随机排序,依次赋值给n个栅格图像R1,R2,…,Rn对应像素R1(x,y),R2(x,y),…,Rn(x,y);
步骤9. 令y=y+1,若y≤Y,则转至步骤3,否则,令y=1;
步骤10. 令x=x+1;若x≤X,则转至步骤3,否则该步骤结束;
步骤11. 输出共享份R1,R2,…,Rn,算法结束.
在算法1中,有2点需要说明:
1) 步骤4~8通过迭代(k,k)-RGVC来实现(k,n)-RGVC,完成单个像素的加密;
2) 步骤7是算法1的核心,由于rk+1,rk+2,…,rn=0,利用元素0是单位元的特性(0⊕0=0,1⊕0=1),当超过k个像素进行运算时,通过叠加白像素避免XOR运算产生的反转效应.
3 (k,n)-RGRIVC方案设计
在第2节的基础上,本节给出RGRIVC的设计流程,分享过程中对于秘密像素s,依据s所在区域的等级,通过随机选取一个授权子集Q对s重新赋值,并利用单秘密RGVC完成像素加密,恢复过程同一般视觉密码方案相同.
3.1秘密分享流程
秘密分享流程如图2所示,具体步骤如下:
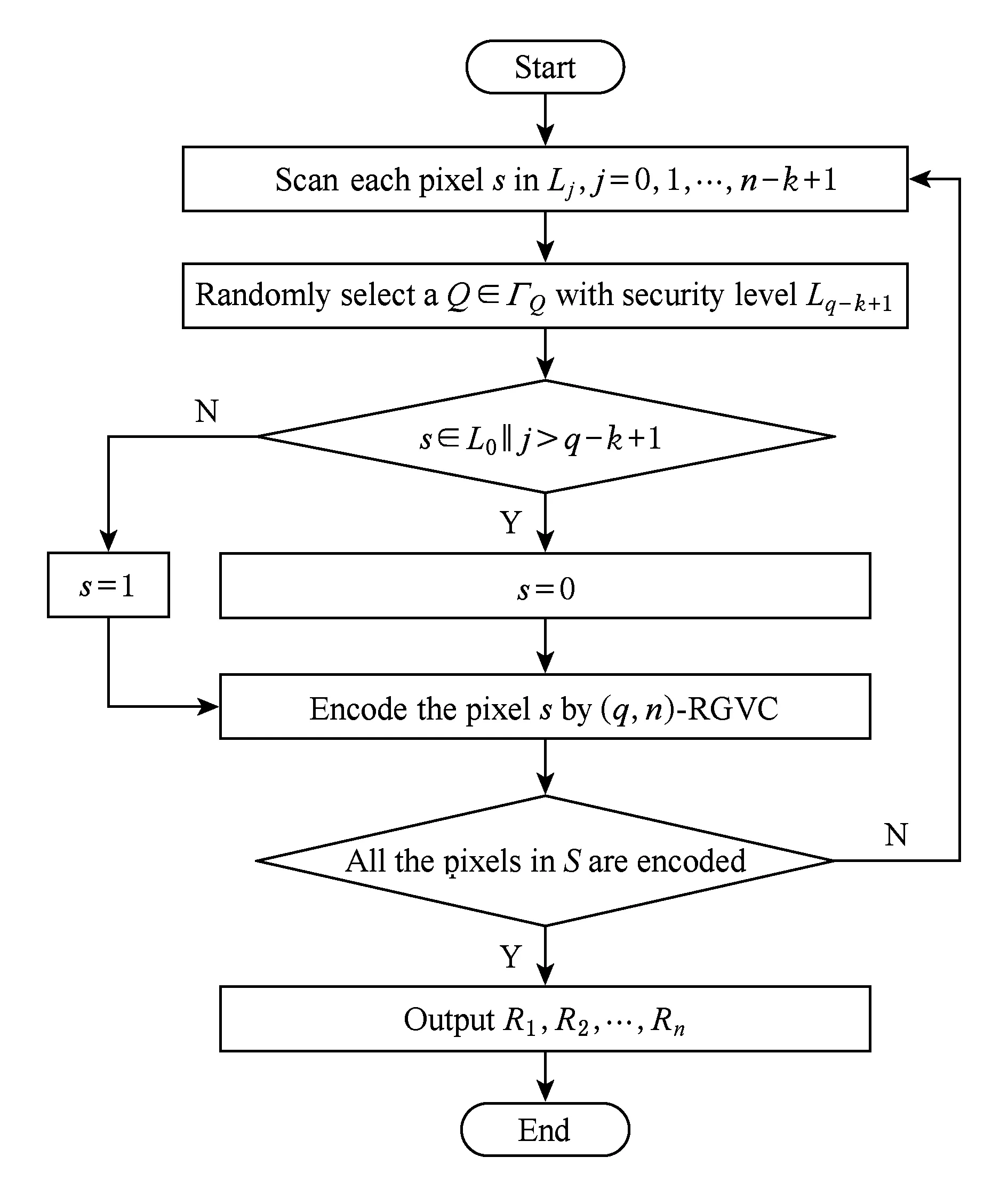
Fig. 2 The secret sharing procedure of RGRIVC.图2 RGRIVC的秘密分享流程
算法2.RGRIVC共享份生成算法.
输入:门限结构(k,n),2≤k≤n,秘密图像S,尺寸大小为X×Y,S=L0,L1,…,Ln-k+1;
输出:共享份Ri,1≤i≤n.
步骤1. 令x=1,x表示正在加密的行号;
步骤2. 令y=1,y表示正在加密的列号;
步骤3. 按行列顺序依次扫描S中区域Lj位置(x,y)的像素s,j=0,1,…,n-k+1,则共享份R1,R2,…,Rn对应位置像素R1(x,y),R2(x,y),…,Rn(x,y)按步骤4~6生成;
步骤4. 随机选取任意授权子集Q={i1,i2,…,iq},Q对应最高密级为Lq-k+1;
步骤6. 利用第2节设计的(q,n)-RGVC对s完成加密;
步骤7. 令y=y+1,若y≤Y,则转至步骤3,否则该步骤结束,令y=1;
步骤8. 令x=x+1,若x≤X,则转至步骤3,否则该步骤结束;
步骤9. 输出共享份R1,R2,…,Rn,算法结束.
3.2秘密恢复流程
当恢复密级为j的区域时,XOR运算任意至少j+k-1个共享份.
4 有效性证明
引理1. 随机选取b位{0,1}随机数,XOR运算后结果是1或0的概率相等,即P(r1⊕2⊕…⊕b=0)=P(r1⊕2⊕…⊕b=1)=12.
证明. 运用数学归纳法,分3步证明:
1) 当b=2时,r1⊕2=r1⊕r2,且P(r1=0)=P(r1=1)=P(r2=0)=P(r2=1)=12.若叠加后恢复像素为白像素,则分为2种情况:①r1=0,r2=0;②r1=1,r2=1,则P(r1⊕2=0)=P(r1=0,r2=0)+P(r1=1,r2=1)=P(r1=0)×P(r2=0)+P(r1=1)×P(r2=1)=12.同理,若叠加后恢复像素为黑像素,同样分2种情况:①r1=0,r2=1;②r1=1,r2=0,则可以得到P(r1⊕2=1)=P(r1=1,r2=0)+P(r1=0,r2=1)=P(r1=1)×P(r2=0)+P(r1=0)×P(r2=1)=12.综上,当b=2时,引理1成立.
2) 假设b=b-1时,引理成立,即P(ri1⊕i2⊕…⊕ib-1=0)=P(ri1⊕i2⊕…⊕ib-1=1)=12,下面证明对于b也成立.
3) 由于rb是随机产生的,故P(rb=0)=P(rb=1)=12.由于r1⊕2⊕…⊕b=r1⊕2⊕…⊕b-1⊕rb,若r1⊕2⊕…⊕b=1,则P(r1⊕2⊕…⊕b=1)=P(r1⊕2⊕…⊕b-1=1)×P(rb=0)+P(r1⊕2⊕…⊕b-1=0)×P(rb=1)=12,若r1⊕2⊕…⊕b=0,则P(r1⊕2⊕…⊕b=0)=P(rb=0)×P(r1⊕2⊕…⊕b-1=0)+P(r1⊕2⊕…⊕b-1=1)×P(rb=1)=12.故假设成立,综上,引理1成立.
证毕.
引理2. 依据算法1(RGVC共享份生成算法)的步骤5~7生成的n个像素r1,r2,…,rn,其中任何一个像素rt不会泄露原像素s的任何信息,t=1,2,…,n,即T(rt[s=0])=T(rt[s=1]).
证明. 分3步证明由算法1中步骤5~7生成的每一位像素都满足此特性:
1) 由算法1的步骤5可知,前k-1位r1,r2,…,rk-1是随机产生的,对于像素r1,P(r1=0)=12,故无论原始像素s是黑或白,满足P(r1=0,s=0)=P(r1=0,s=1)=12.同理可证,对于像素r2,…,rk-1也成立,故r1,r2,…,rk-1不会泄露原像素的任何信息.
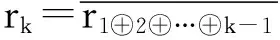
3) 由算法1的步骤7可知,对于rk+1,…,rn,不妨以rk+1为例,不论原始像素是黑或白,满足rk+1=s⊕r1⊕r2⊕…⊕rk-1⊕rk=rk⊕rk=0,故P(r1=0,s=0)=P(r1=0,s=1)=1,同理可知,rk+2,rk+3,…,rn=0,上述结果也成立.
证毕.
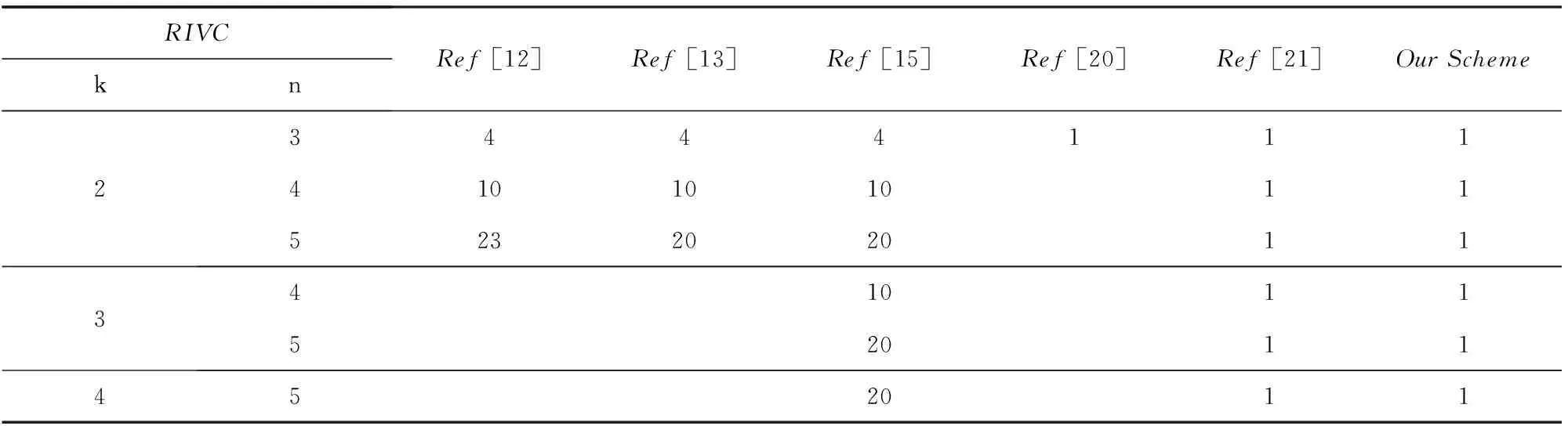
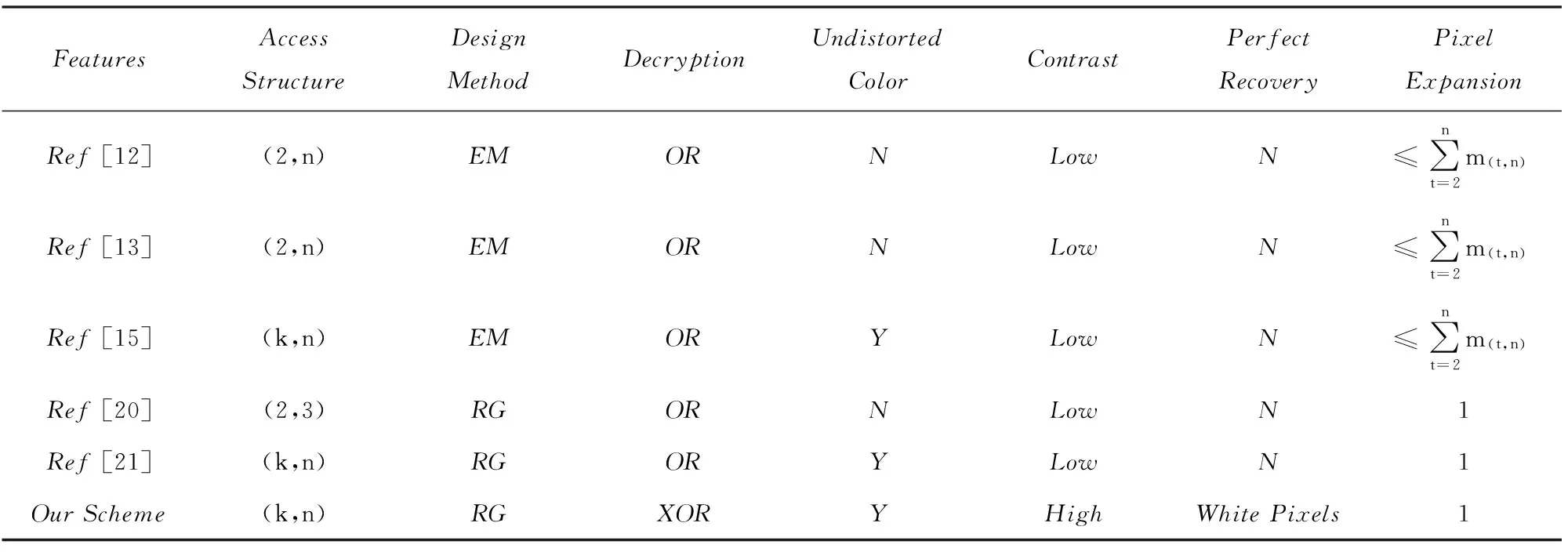
引理3. 依据算法1(RGVC共享份生成算法)的步骤5~7生成的n个像素r1,r2,…,rn,其中任意t 证明. 由于rk+1,rk+2,…,rn都为0,且0与任何元素XOR运算结果不变,故这里仅考虑t个元素ri1,ri2,…,rit⊂{r1,r2,…,rk}的情况,分rk∈{ri1,ri2,…,rit}和rk∉{ri1,ri2,…,rit}两种情况说明: 1) 当rk∈{ri1,ri2,…,rit}时,不妨设rit=rk,{g1,g2,…,gh}={1,2,…,k-1}-{i1,i2,…,i(t-1)},可得: ri1⊕i2⊕…⊕it=ri1⊕ri2⊕…⊕rit= ri1⊕ri2⊕…⊕ri(t-1)⊕rk= ri1⊕…⊕ri(t-1)⊕(s⊕r1⊕…⊕rk-1)= ri1⊕…⊕ri(t-1)⊕(s⊕ri1⊕ri2⊕…⊕ ri(t-1)⊕rg1⊕rg2⊕…⊕rgh)= s⊕rg1⊕…⊕rgh. 由于rg1,rg2,…,rgh是通过算法1的步骤5随机生成的,结合引理1可知,P(rg1⊕rg2⊕…⊕rgh=0)=P(rg1⊕rg2⊕…⊕rgh=1)=12.当s=0时,ri1⊕ri2⊕…⊕rit=rg1⊕rg2⊕…⊕rgh,表明P(rri1⊕ri2⊕…⊕rit=0)=P(rri1⊕rri2⊕…⊕rit=1)=12;当s=1时,ri1⊕ri2⊕…⊕,故P(ri1⊕i2⊕…⊕it=0)=P(rg1⊕rg2⊕…⊕rgh=1)=12,P(ri1⊕i2⊕…⊕it=1)=P(rg1⊕rg2⊕…⊕rgh=0)=12.综上,可得T(ri1⊕i2⊕…⊕it[s=0])=T(ri1⊕i2⊕…⊕it[s=1]). 2) 当rk∉{ri1,ri2,…,rit}时,由步骤5,ri1,ri2,…,rit都是随机产生的,结合引理1可知, T(ri1⊕i2⊕…⊕it[s=0])=T(ri1⊕i2⊕…⊕it[s=1]). 证毕. 引理4. 依据算法1的步骤5~7生成的n个像素r1,r2,…,rn,其中任意t≥k个像素XOR运算,满足T(ri1⊕i2⊕…⊕it[s=0])>T(ri1⊕i2⊕…⊕it[s=1]). 证明. 设t个像素ri1,ri2,…,rit中有u个是从r1,r2,…,rk中取得的,另外v个是从rk+1,rk+2,…,rn中取得的,分2种情况考虑:1)u=k,v=t-k;2)u 综合上述2种情况,任意t个像素XOR运算后原始白像素的光通量为 T(u=k)(ri1⊕i2⊕…⊕it[s=0])+ T(u 黑像素的光通量为 T(u=k)(ri1⊕i2⊕…⊕it[s=1])+ T(u 由于T(u=k)(ri1⊕i2⊕…⊕it[s=0])>T(u=k)(ri1⊕i2⊕…⊕it[s=1]),T(u 证毕. 证毕. 定理1. 依据算法1设计的单秘密(k,n)-RGVC满足3个条件: 1) 单个共享份不泄露秘密图像的任何信息,即T(Rt[S(0)])=T(Rt[S(1)),t=1,2,…,n; 2) 任意t 3) 任意t≥k共享份XOR运算可以恢复秘密图像,即T(Ri1⊕i2⊕…⊕it[S(0)])>T(Ri1⊕i2⊕…⊕it[S(1)]). 证明. 1) 由引理2可知,对于任意共享份Rt中的一个生成像素r,t=1,2,…,n,满足T(r[s=0])=T(r[s=1]). 结合定义2可知,条件1)成立. 2) 由引理3可知,当t 3) 由引理4可知,当t≥k时,任意t个像素XOR运算后,满足T(ri1⊕i2⊕…⊕it[s=0])>T(ri1⊕i2⊕…⊕it[s=1]),由定义1可知,条件3成立. 证毕. 定理2. 依据算法2设计的(k,n)-RGRIVC满足2个条件: 证毕. 推论1. 当R1,R2,…,Rn进行XOR运算后,秘密图像S中白色区域L0能够完美恢复,满足T(R1⊕2⊕…⊕n[S(0)])=1. 证明. 对于区域L0中的任意像素s,依据算法2的步骤5可知,像素s=0,加密后生成的n个子像素r1,r2,…,rn中,前k个像素由算法2的步骤4~6生成,满足r1⊕r2⊕…⊕rk=0,后面n-k个像素rk+1,rk+2,…,rn由算法2的步骤7生成,满足rk+1,rk+2,…,rn=0.因此,像素r1,r2,…,rn满足r1⊕r2⊕…⊕rn=r1⊕r2⊕…⊕rk⊕rk+1⊕…⊕rn=r1⊕r2⊕…⊕rk⊕0=r1⊕r2⊕…⊕rk=0,故T(r1⊕2⊕…⊕n[s=0])=1,结合定义2可知T(R1⊕…⊕n[S(0)])=1,故所有共享份XOR运算后,原始白像素的光通量为1,实现了完美恢复. 证毕. Table 2 The Experiment Results of (2,3)-RIVC表2 (2,3)-RIVC的实验效果 Continued (Table 2) 1) 单个共享份是杂乱无章的,不会泄露秘密图像的任何信息,且不存在像素扩展,任意2个共享份进行XOR运算后,可以恢复区域L1,所有共享份进行XOR运算后,可以同时恢复区域L1和L2,与预期结果相同. 2) 在恢复效果方面,文献[20]恢复图像中白像素的颜色比黑像素的颜色深,说明恢复图像存在色彩反转失真,本方案恢复图像不存在色彩反转失真,可以正确反映秘密图像的颜色信息.依据定义3,通过统计分析可知,2个共享份叠加后,文献[21]中区域L1的对比度为0.146,本方案为0.182; 3个共享份叠加后,文献[21]中区域L1和L2的对比度分别为0.336和0.152,而本方案为1和0.170,显然本方案对比度更高.可以看出文献[21]恢复图像的背景色偏暗,图像模糊,而本方案明显更清晰.特别地,所有共享份XOR运算,原白像素实现了完美恢复,同时区域L1的黑像素也实现了完美恢复. 本方案与其他区域递增式视觉密码方案的比较见表3~5所示. 1) 在存取结构方面,文献[15,21]和本方案适用于任意(k,n)门限结构,因此应用场景更丰富. 2) 在设计方法方面,文献[12-13,15]基于加密矩阵设计,由于构造矩阵的约束条件极其复杂,随着参与者人数的增加,矩阵规模急剧增大,如表4所示,因而需要额外的计算设备来完成矩阵构造.而本方案基于随机栅格设计,秘密分享过程仅利用随机函数,设计方法丰富,避免了生成和保存加密矩阵产生的额外开销. Table 3 Comparison of Contrast among Our Scheme with Ref [20-21]表3 本方案与文献[20-21]对比度的比较 Table 4 Comparison of Pixel Expansion among Our Scheme with Others表4 本方案与其他方案像素扩展度的比较 Table 5 Comparison of Features among Our Scheme with Others表5 本方案与其他方案的特点比较 3) 在解密算法方面,只有本方案适用于XOR运算.XOR运算不违背视觉密码恢复简单性的原则,随着具有简单计算能力的智能终端的日益普及,基于XOR操作的方案使用将更加方便,应用前景更加广阔. 4) 在色彩失真方面,文献[12-13,20]存在颜色反转失真,而本方案可以正确显示原始图像颜色的真实信息. 5) 在区域识别效果方面,表3列出不同门限结构下本方案和同类像素不扩展方案平均对比度的统计分析结果,显然,本方案的对比度高于文献[20-21].以(3,4)方案为例,本方案的最高对比度为1,最低对比度为0.147,现有最优方案分别为0.226和0.035,可见本方案对比度高,因此恢复效果更清晰. 6) 在完美恢复方面,当所有共享份叠加时,本方案能够实现秘密图像中白像素的完美恢复. 7) 在像素扩展度方面,表5中m(t,n)表示(t,n)单秘密VC的像素扩展度,文献[13,15]的像素扩展度为单秘密方案像素扩展度的线性组合(删除其中的冗余列),文献[12]未给出具体构造方法.为进一步说明,表4列出了不同门限结构下本方案与其他方案像素扩展的具体比较结果,可以看出,文献[12-13,15]的像素扩展度随着k和n的增加而迅速增大,相比之下,本方案不存在像素扩展,实现了共享份存储和传输开销最优化. 本文对区域递增式视觉密码进行了研究,结合异或运算,给出了(k,n)-RGRIVC的实现方案,并对方案的有效性进行了理论证明和实验验证.该方案通过迭代(k,k)-RGVC,设计基于异或运算的(k,n)-RGVC,并构造了秘密图像的分享和恢复流程,在像素不扩展的前提下有效提高了恢复图像的对比度. [1]NaorM,ShamirA:Visualcryptography[G] //LNCS950:AdvancesinCryptology-Eurocrypt’94.Berlin:Springer, 1995: 1-12 [2]AtenieseG,BlundoC,SantisAD,etal.Visualcryptographyforgeneralaccessstructures[J].InformationandComputation, 1996, 129(2): 86-106 [3]WangDS,ZhangL,MaN,etal.TwosecretsharingschemesbasedonBooleanoperations[J].PatternRecognition, 2007, 40(10): 2776-2785 [4]LiuF,WuC,LinX.Stepconstructionofvisualcryptographyschemes[J].IEEETransoninformationforensicsandsecurity, 2010, 5(1): 27-38 [5]ShyuSJ,JiangHW.Generalconstructionsforthresholdmultiple-secretvisualcryptographyschemes[J].IEEETransonInformationForensicsSecurity, 2013, 8(5): 733-743 [6]FuZhengxin,YuBin,FangLiguo.Anewmulti-secretsharingvisualcryptography[J].ActaElectronicaSinica, 2011, 39(3): 712-718 (inChinese) (付正欣, 郁滨, 房礼国. 一种新的多秘密分享视觉密码[J]. 电子学报, 2011, 39(3): 712-718) [7]YuB,ShenG.Multi-secretvisualcryptographywithdeterministiccontrast[J].MultimediaToolsandApplications, 2014, 72(2): 1867-1886 [8]ChenYC,TsaiDS,HorngG.AnewauthenticationbasedcheatingpreventionschemeinNaor-Shamir’svisualcryptography[J].JournalofVisualCommunicationandImageRepresentation, 2012, 23(8): 1225-1233 [9]WuX,SunW.Randomgrid-basedvisualsecretsharingwithabilitiesofORandXORdecryptions[J].JournalofVisualCommunicationandImageRepresentation, 2013, 24(1): 48-62 [10]ShenGang,FuZhengxin,YuBin.Onthegeneralityof(k, n)XOR-basedvisualcryptographyscheme[J].JournalofElectronics&InformationTechnology, 2013, 35(10): 2294-2300 (inChinese) (沈刚, 付正欣, 郁滨. (k, n)异或视觉密码的一般性研究[J]. 电子与信息学报, 2013, 35(10): 2294-2300) [11]YangCN,WangDS.PropertyanalysisofXORbasedvisualcryptography[J].IEEETransonCircuitsandSystemsforVideoTechnology, 2014, 24(2): 189-197 [12]WangRZ.Regionincrementingvisualcryptography[J].IEEESignalProcessingLetters, 2009, 16(8): 659-662 [13]ShyuSJ,JiangHW.Efficientconstructionforregionincrementingvisualcryptography[J].IEEETransonCircuitsandSystemsforVideoTechnology, 2012, 22(5): 769-777 [14]YangCN,ShihHW,ChuYY,etal.Newregionincrementingvisualcryptographyscheme[C] //Procofthe18thIntConfonImageProcessing,ComputerVision,andPatternRecognitioninConjunctionwithWORLDCOMP.Piscataway,NJ:IEEE, 2011: 323-329 [15]YangCN,ShihHW,WuCC,etal. koutofnregionincrementingschemeinvisualcryptography[J].IEEETransonCircuitsandSystemsforVideoTechnology, 2012, 22(5): 799-810 [16]YangCN,LinYC,WuCC:Region-in-Regionincrementingvisualcryptographyscheme[G] //LNCS7809:Procofthe12thIntWorkshoponDigital-ForensicsandWatermarking.Berlin:Springer, 2013: 449-463 [17]LiJiliang,LiShundong,WangDaoshun.Constructionofregionincrementingvisualcryptography[C//OL]. [2015-08-27].http://wenku.it168.com//d_001561197.shtml(inChinese) (李吉亮, 李顺东, 王道顺. 区域递增视觉密码的构造 [C//OL]. [2015-08-27].http://wenku.it168.com//d_001561197.shtml) [18]ShyuS.Imageencryptionbyrandomgrids[J].PatternRecognition, 2007, 40(3): 1014-1031 [19]ShyuS.Imageencryptionbymultiplerandomgrids[J].PatternRecognition, 2009, 42(7): 1582-1596 [20]WangRZ,LanYC,LeeYK,etal.Incrementingvisualcryptographyusingrandomgrids[J].OpticsCommunications, 2010, 283(21): 4242-4249 [21]ZhongGS,WangJJ.Regionincrementingvisualsecretsharingschemebasedonrandomgrids[C] //Procof2013IEEEIntSymponCircuitsandSystems.Piscataway,NJ:IEEE, 2013: 2351-2354 HuHao,bornin1989.PhDcandidate.Hismainresearchinterestsincludevisualcryptography,situationalawarenessandcyberspacesecurity. ShenGang,bornin1986.PhDcandidate.Hismainresearchinterestsincludevisualcryptographyandinformationsecurity. YuBin,bornin1964.PhDandprofessor.Hismainresearchinterestsincludethedesignandanalysisofalgorithms,visualcryptographyandnetworksecurity. MahaoJunfu,bornin1989.BScandassistantengineer.Hismainresearchinterestisinformationsecurity. XOR-BasedRegionIncrementingVisualCryptographySchemebyRandomGrids HuHao,ShenGang,YuBin,andMahaoJunfu (College of Cryptography Engineering, Information Engineering University, Zhengzhou 450001) Consideringtheproblemofthewhitepixelsinsecretimagescannotbecorrectlyrecovered,whichisresultedbytheORoperationconfinedinexitingregionincrementingvisualcryptographyschemes,anoveldefinitionofregionincrementingvisualcryptographybasedonXORoperationisproposedforthefirsttime.Byiteratingrandom-grid-based(k,k)single-secretvisualcryptographyschemeandcombingthepropertyof0asthegeneratorofthe{0, 1}group,thesharesgenerationalgorithmof(k,n)single-secret-sharingschemeusingXORoperationisdesigned,andthesecretsharingandrecoveringproceduresforregionincrementingschemeareproposedfurther.Foranyoriginalsecretpixels,accordingtothesecuritylevel, sisreassignedassociatedwitharandomlychosenqualifiedsetQinthesharingprocedure,andthenencodedbytheproposed(k,n)single-secret-sharingscheme.Therecoveringprocedureisthesameasthatofthepreviousschemes.Theeffectivenessistheoreticallyverifiedatlast.Experimentalresultsshowthatthepresentschemenotonlyrealizesnopixelexpansion,butalsocanobtaintheperfectrecoveryofwhitepixelswhenallthesharesarestacked. imagesecretsharing;visualcryptography;securitylevel;regionincrement;randomgrid;XOR 2015-01-19; 2015-09-16 国家自然科学基金项目(61070086);信息保障技术重点实验室开放基金项目(KJ-13-107) TP309 ThisworkwassupportedbytheNationalNaturalScienceFoundationofChina(61070086)andtheFoundationofScienceandTechnologyonInformationAssuranceLaboratoryofChina(KJ-13-107).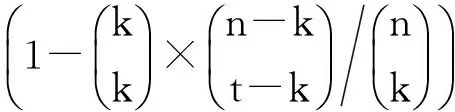
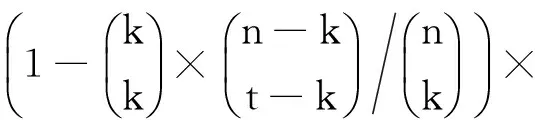
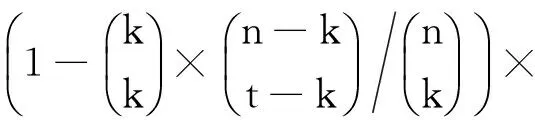
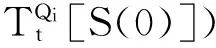
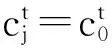
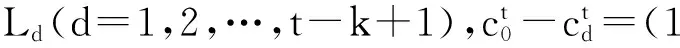
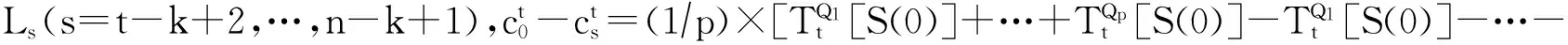
5 实验与分析
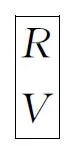


6 结束语





