指数为3和5的费尔马大定理第一情形的一种简单初等证明
梁济明
(贵阳学院 继续教育学院,贵州 贵阳 550005)
指数为3和5的费尔马大定理第一情形的一种简单初等证明
梁济明
(贵阳学院 继续教育学院,贵州 贵阳 550005)
用初等乘法公式给出指数为3和5时费尔马大定理第一情形的一种简单初等证明;类似方法可推广到更高素指数,得到费尔马大定理第一情形的一种“奇妙”解决思路。
简单初等证明;费尔马大定理第一情形;一种解决思路
一、引言
费尔马大定理,更多被叫做费尔马最后定理(Fermat’ Last Therom),就是指:在n为大于2的正整数时,方程xn+yn=zn没有关于x、y、z的正整数解。当n不整除xyz时,被叫作“第一情形”。本文给出方程x3+y3=z3在3不整除xyz时,没有关于x、y、z的正整数解的一种巧妙的简单初等证明,尝试由此特殊证法引申推广到指数为5的情况,找到证明费尔马大定理第一情形的一种解决思路。
二、方程x3+y3=z3当3不整除xyz时,没有正整数解的证明
证明:
(一)方程x3+y3=z3的预备知识讨论
假设存在一组正整数解x、y、z满足方程:
x3+y3=z3
①
若x、y有1以上的正整数公因子d,即:
(x,y)=d>1
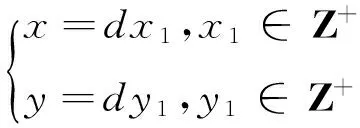
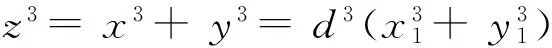
⟹d|z=dz1,z1∈Z+
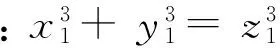
且:(x1,y1)=(x1,y1)=(y1,z1)=1
∴以下仅证明方程 ① 没有x、y、z两两互质的正整数解。
我们定义这样的一组正整数解为:费尔马方程的基本解。
(二)方程x3+y3=z3的特殊性质
从初中学生就掌握的多项式乘法公式出发,有如下恒等式:
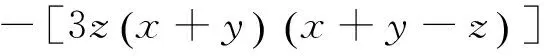
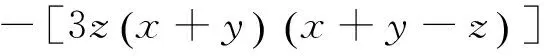
②
∵假设①成立,即 ① 有费尔马方程基本解,满足:x3+y3=z3⟺x3+y3-z3=0
代入② 式右边,得到:
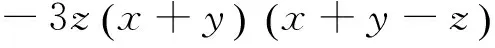
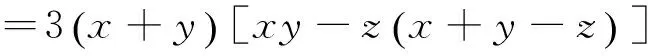
③
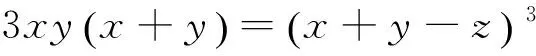
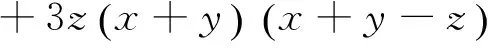
④
奇妙的是,显然有 :
∵3是素数
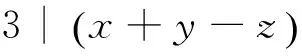
⑤
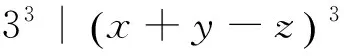
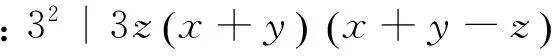
⟹32|④式右边
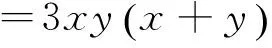
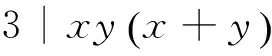
⑥
(三)第一情形:当3不整除xyz时
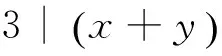
同时由⑤式⟹3|z
∴⟹3|xyz,此与第一情形3不整除xyz矛盾。
由此得证
结论1:不存在没有因数3的一组正整数解x、y、z,
满足方程:x3+y3=z3
三、方程x5+y5=z5当5不整除xyz时,没有正整数解的证明
证明:
类似地,运用同上述证明过程一样的方法,有如下恒等式:
⑦
假设存在一组正整数基本解x、y、z满足方程:
x5+y5=z5⟺x5+y5-z5=0
代入⑦ 式右边,得到:
=5xy(x+y)(x2+xy+y2)
⑧
仍然奇妙的是,显然有:
⟹5|⑧式右边
∵5是素数
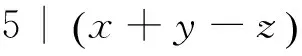
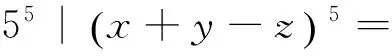
⟹55|⑧式右边
⟹52|⑧式右边
注意到:⑧式右边后一项含有因数5及因子(x+y-z)
⟹52|5xy(x+y)(x2+xy+y2)
⟹5|xy(x+y)(x2+xy+y2)
在第一情形:当5不整除xyz时
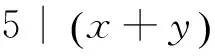
∴⟹5|xyz,此与第一情形5不整除xyz矛盾。

⟹5|(x2+xy+y2)
⟹x2+xy+y2=5k, 这里k是正整数
⟹(x2+y2)2=(5k-xy)2
⟹x4+2x2y2+y4=52k2-2(5k)xy+x2y2
⟹x4+x2y2+y4=5(5k2-2kxy)
⟹5|(x4+x2y2+y4)
⟹5|[(x4-1)+(y4-1)+(x2y2+2)]
⑨
∵5不整除xyz,
由费尔马小定理(其初等证明参见参考文献[2]),
即任意奇素数p若不整除正整数a,则成立:
p|(ap-1-1)
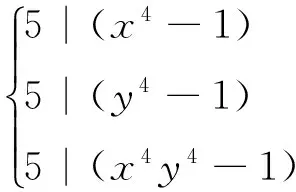
⑩
将 ⑩ 式代入 ⑨式:
⟹5|(x2y2+2)
⟹5|[(x2y2+2)(x2y2-2)]
⟹5|(x4y4-4)
此式与⑩式中第三式相加:
⟹5|[(x4y4-4)+(x4y4-1)]
⟹5|(2x4y4-5)
⟹5|2x4y4
⟹5|xy,此与第一情形5不整除xyz矛盾。
由此得证
结论2:不存在没有因数5的一组正整数解x、y、z,
满足方程:x5+y5=z5
三、结束语
费尔马在大约1637年左右阅读丢番图《算术》拉丁文译本时,曾在第11卷第8命题旁留下一段文字“将一个立方数分成两个立方数之和,或一个四次幂分成两个四次幂之和,或者一般地将一个高于二次的幂分成两个同次幂之和,这是不可能的。关于此,我确信已发现了一种美妙的证法,可惜这里空白的地方太小,写不下。”这不由让人们认为,他当时找到的证明不会太复杂也不会太长。尽管英国数学家怀尔斯1995年用高深复杂且只有少数人能读懂的上百页证明过程解决了这个“费尔马大定理”。
本文证明过程为了便于中学生能阅读,仅用到乘法公式和整除的概念及已有初等证明的费尔马小定理,当然可以作为中学练习题或竞赛题。对于得证结论:“方程x3+y3=z3当3不整除xyz时,没有关于x、y、z的正整数解”,其几何含意是:任意两个边长是不含有因数3的整数的立方体的体积之和,不可能是另一个边长也是不含有因数3的整数的更大立方体的体积。
事实上,对任意素数p为指数的费尔马大定理第一情形,还是用同样方法,仍然成立:
⟹p2|[(x+y)p-zp]
⟹…
…
⟹矛盾。
这是不是费尔马最初的“奇妙”证法呢?
[1]闵嗣鹤,严士健.初等数论(第二版)[M] .北京:高等教育出版社:1982.
[2]梁济明.费尔马小定理的初等证明[J] .贵阳金筑大学学报,2005(2):109.
A simple primary proof of Fermat'Last Therom first situation when the index is 3 and 5
LIANG Ji-ming
(School of Continuing Education, Guiyang University, Guizhou,Guiyang 550005,China)
A simple primary proof of Fermat' Last Therom first situation is given by the primary multiplicationwhen the index is 3 and 5,so the simple way may be used for more advanced prime index to get a wonderful idea solution of Fermat' Last Therom first situation.
The Simple primary certificate;The first situation of Fermat' Last Therom;The idea of a way to deal
2016-09-11
梁济明(1963-),男,广西梧州人,贵阳学院副教授。主要研究方向:数学与计算机教学及研究。
O156
A
1673-6125(2016)04-0001-03

