利用Eξ2≥(Eξ)2证明含n项和的不等式
吴邦昆
(合肥职业技术学院,安徽 巢湖 238000)
利用Eξ2≥(Eξ)2证明含n项和的不等式
吴邦昆
(合肥职业技术学院,安徽 巢湖 238000)
使用常规方法证明含n项和的代数不等式,往往技巧大,过程复杂。如果合理利用概率论中的Eξ2≥(Eξ)2结论证明这类不等式,可以开辟证明方法的新途径,其证法构思新奇,思路清晰,富于规律,易于掌握。
方差;证明;不等式
设ξ是一个只取有限个值a1,a2,a3,…,an的离散型随机变量,其概率分布为p(ξ=ai)=pi﹥0,i=1,2,3,…,n则ξ的方差为

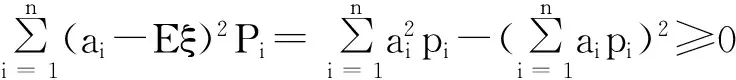

当且仅当a1=a2=a3=…=an=Eξ时等号成立。
证明一类含有n项和的代数不等式时,根据具体不等式的特点,构造相应的随机变量及其概率分布列,利用上述方差性质Eξ2≥(Eξ)2,使得不等式的证明过程构思新奇,思路清晰,具有独特而简洁的功效。现举例如下:
例1:设xi≥0,i=1,2,3,…,n则
当且仅当x1=x2=x3=…=xn时等号成立


两边开方即得所证不等式,当且仅当x1=x2=x3=…=xn时等号成立。
例2:设xi>0,i=1,2,3,…,n,则
当且仅当x1=x2=x3=…=xn时等号成立。









∵Eξ2≥(Eξ)2
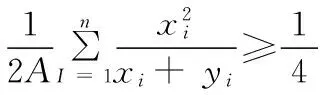
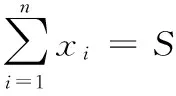

当且仅当x1=x2=x3=…=xn时等号成立。
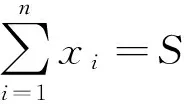


∵Eξ2≥(Eξ)2
至于什么时候聚,怎么聚,周教授已经安排好了,他说时间么就定在中午,地点么就到郊外,他远房侄儿周青才开不久的桃花源农庄。周教授强调说,现在正值春天,桃花源的风景很好,我们正好都做一回陶渊明么。几个电话里都说好,让周教授等着,他们都到周教授住宅小区门口集合,然后再一起去桃花源农庄。
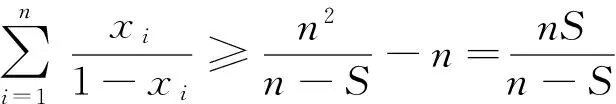
当且仅当x1=x2=x3=…=xn时等号成立,原不等式得证。

证明:设随机变量ξ的概率分布列为:
∵Eξ2≥(Eξ)2



而此式显然成立,原不等式得证。


证明:设随机变量ξ的概率分布列为:

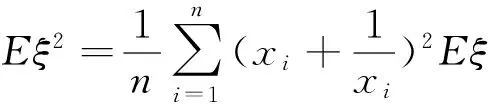
∵Eξ2≥(Eξ)2
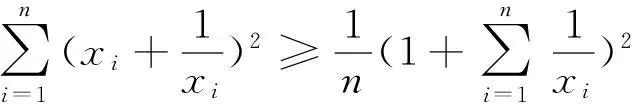

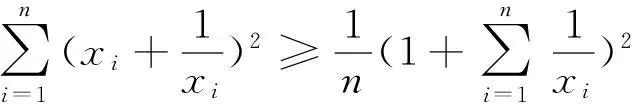
原不等式得证。
[1]朱胜强.浅谈不等式证明的非常规方法[J].中学数学,2004(8):20-21.
[2]李向东.由柯西不等式的证明所想到的[J].中学数学,1997(8).
[3]周松.猜想与构造在对称不等式中的运用[J].中学数学,2005(7).
[4]江勤瑜.探究数学解题思路,培养创造思维能力[J].中学教研(数学),1998(3):7-9.
[5]邓国强.促进思维迁移 提高解题能力[J].中学数学研究,1995(7):28.
[6]谭维奇.高等数学(下册)[M].南京:江苏人民出版社,2008.
[7]夏国斌.高等数学[M].合肥:安徽大学出版社,2006.
Employment ofEξ2≥(Eξ)2to prove inequalities containing n terms
WU Bang-kun
(Hefei Vocational and Technical College, Hefei Anhui 238000,China)
It is intricate to prove algebraic inequalities containing n terms through conventional methods. TheEξ2≥(Eξ)2conclusion of probability theory provides a novel method to prove this kind of inequalities, and the proving process is clear, logical and easy to grasp.
variance; prove; inequality
2016-08-24
安徽省高校省级质量工程项目:“高等数学”精品资源共享课程(项目编号:2013gxk161);合肥职业技术学院质量工程项目“高等数学”精品课程(项目编号:JPKC201302);安徽省高校人文社科重点项目:“大数据背景下高职学生学习力研究”(项目编号:SK2015A734)。
吴邦昆(1964-),男,安徽庐江人,副教授。主要研究方向:高等数学。
O151.25
A
1673-6125(2016)04-0004-02

