几种三角习题变换的推广
金 凤
(贵州轻工职业技术学院,贵州 贵阳 550025)
几种三角习题变换的推广
金 凤
(贵州轻工职业技术学院,贵州 贵阳 550025)
引导学生发现三角函数的许多习题是可以互相转化或延伸的, 对于学习巩固所学知识, 活跃思维, 扩大知识覆盖面, 培养举一反三、触类旁通的能力等方面都是非常有益的。
三角习题;变换;推广
在三角函数教学中特别是上复习题课时,引导学生发现三角函数的许多习题是可以互相转化或延伸的,对于学习巩固所学知识,活跃思维,扩大知识覆盖面,培养举一反三、触类旁通的能力等方面都是非常有益的。笔者就以下几种三角函数习题的变化进行说明:
例1:在△ABC中,如果三边a、b、c 成等差数列,则有:
一、重组命题
(1)sinA、sinB、sinC成等差数列
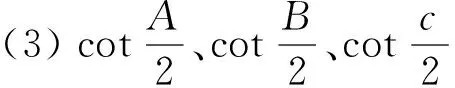
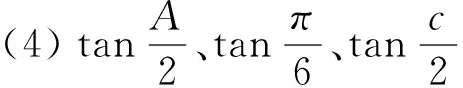
例题包括一个已知条件和7 个结论共8 个命题,每两个命题都互为充要条件,因而可以组成56 个不同的习题。
例1: 在△ ABC 中,如果sinA、sinB、sinC成等差数列,则a、b、c 也成等差数列。
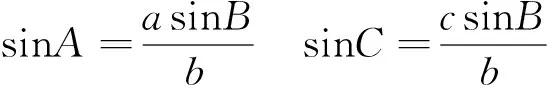
已知2sinB=sinA+sinC
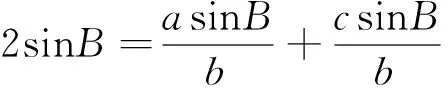
即 2b=a+c
∴ 此命题得证
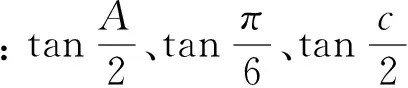
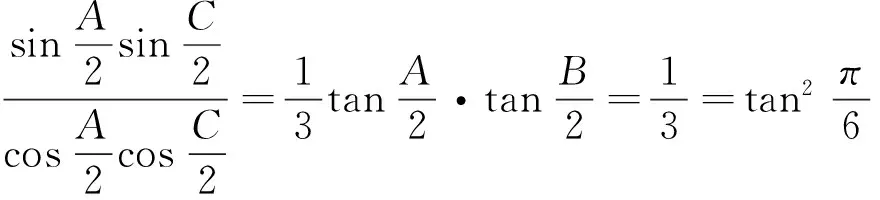
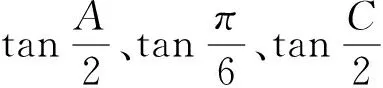
例3:在△ ABC 中,如果tanA、tanB、tanc成等差数,则
(1)tanA·tanC=3
(2)sin2A、sin2B、sin2C成等差数
(3)若O为锐角三角形ABC的外心,则SΔBOC、SΔAOC、SΔBOC成等差数
(4)△ ABC为锐角三角形
本例题包括一个已知条件和四个结论,除命题(4 ) 为其他命题的必要条件外,其余的每两个均可互为充要条件,因而可组成16个不同的习题。
例如1:在△ ABC 中,如果tanA·tanC=3,求证:tanA、tanB、tanc成等差数
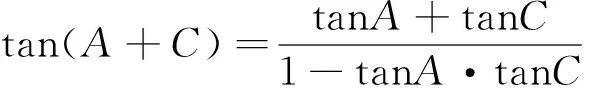
二、延伸结论
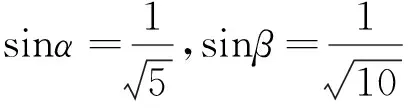
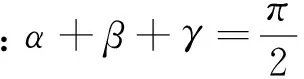
还可以延伸为证明用反三角函数表示的等式
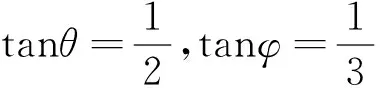
此题可延伸为
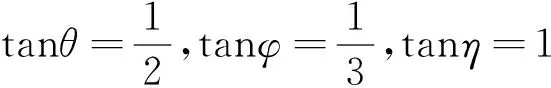
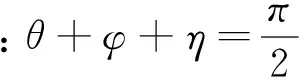
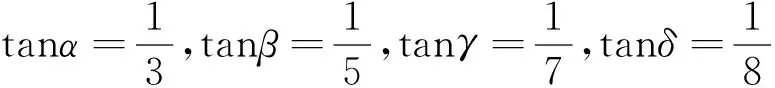
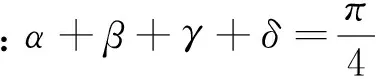
还可以延伸为证明用反三角函数表示的等式
三、利用“1”的多变性求解
“1”的多变性在三角函数中的运用是很突出的。如
1=sin2α+cos2α,1=tanα·cotα,1=sec2α-tan2α,1=2cos2α-cos2α,1=cos0等等。
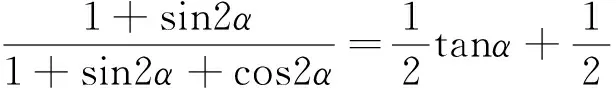
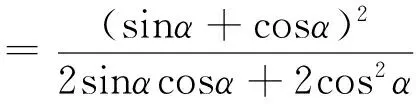
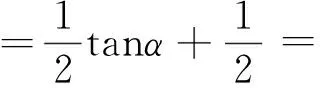
∴此题得证
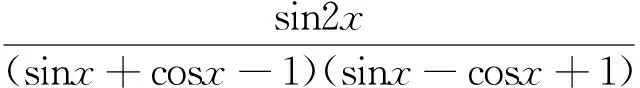
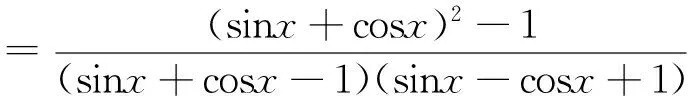
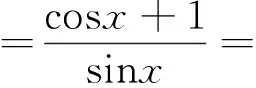
∴此题得证
四、在三角形中的变换
在三角形的计算或证明中,常用到勾股定理、正弦定理、余弦定理、射影定理、诱导公式等引出的各种公式。
在△ ABC 中由射影定理c=acosB+bcosA,b=acosC+ccosA,a=bcosC+ccosB
还可以根据需要变换成各种边与角的关系
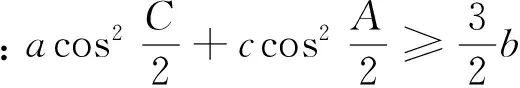
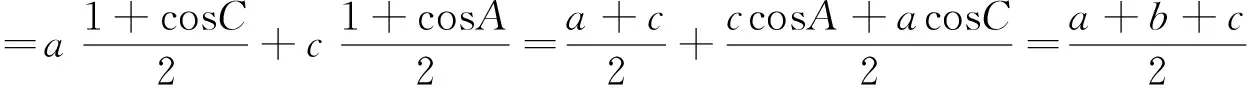
因为a、b、c成等比数列,
∴a+c≥2b
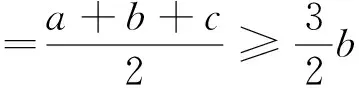
∴结论成立
例9:在 △ ABC中,已知A、B和周长2p,求a、b、c
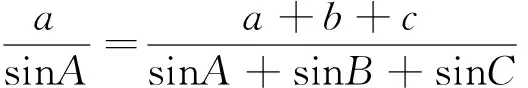
且:a+b+c=2c
sinA+sinB+sinC
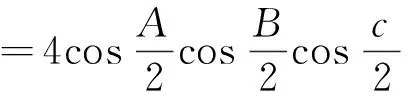
同理可得:
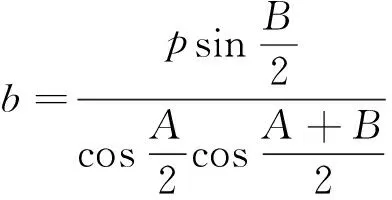
[1]金凤. 几种三角习题的变换[J]. 成都教育学院学报, 2002(12) :67-68.
[2]傅荣强.龙门专题高中数学三角函数[M].北京:龙门书局,2014.
On the promotion of the transformation of several trigonometric exercises golden phoenix
JIN Feng
(Guizhou Institute of Light Industry Guiyang Guizhou 550025,China)
Guide students to discover many exercises trigonometric functions can be transformed into each other or extend, consolidate the knowledge for learning, active thinking, expand knowledge coverage, giving top priority to culture, capacities, etc. are very useful analogy.
Triangle problem sets;integral transform;Promotion
2016-09-09
金 凤(1965-),女,贵州贵阳人,副教授。主要研究方向:高等数学。
O174
A
1673-6125(2016)04-0006-03

