一类时滞SIRS网络病毒传播模型的周期解

张子振，谢伟杰，江 月，李佳倩，赵 涛

(安徽财经大学 管理科学与工程学院，安徽 蚌埠 233030)

一类时滞SIRS网络病毒传播模型的周期解

张子振，谢伟杰，江 月，李佳倩，赵 涛

(安徽财经大学 管理科学与工程学院，安徽 蚌埠 233030)

本文研究了一类时滞SIRS计算机网络病毒传播模型。首先确定了模型产生Hopf分支的时滞临界点。然后利用中心流形定理和规范型理论得到了确定Hopf分支的方向、稳定性和分支周期解周期大小的显性计算公式。最后，利用仿真示例验证了所得结果的正确性。

SIRS模型；网络病毒；周期解

1 引言

近年来，互联网的快速发展为人们的日常工作和日常生活的各个方面都带来了诸多便利。与此同时，随着互联网应用的不断发展，以及计算机网络复杂性的不断增长，计算机网络安全问题日益显著。受传染病学领域研究工作的启发，并考虑到网络病毒在网络中计算机之间的传播与生物病毒在社会中个体之间的传播相似性，不少传染病模型被借助于研究网络病毒的传播规律[1-4]。但是，以上对网络病毒传播模型的研究均未考虑网络病毒在计算机网络传播过程中的延迟时滞因素。因此，研究具有时滞的计算机网络病毒传播模型[5-7]，对于有效控制计算机网络病毒的传播，更加具有现实意义。考虑到清除已感染计算机中的病毒需要一个时间周期，以及处于恢复状态的计算机具有一定的临时免疫期，文献[7]研究了如下具有直接免疫的时滞SIRS计算机网络病毒传播模型的Hopf分支的存在性：

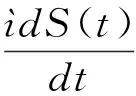
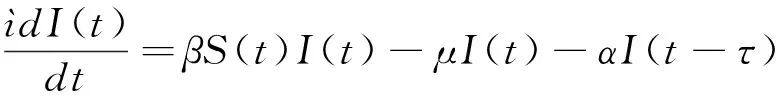
(1)

其中，S(t)表示处于易感染状态的计算机在时刻t的数量,I(t)和R(t)分别表示已感染的计算机和处于恢复状态的计算机在时刻t的数量。A,p,α,β,γ,δ和μ为系统(1)的参数，均具有和文献[5]相同的含义。τ是因清除网络病毒而需要的时间周期以及恢复状态的计算机具有的临时免疫期而存在的时滞。文献[5]讨论了系统(1)Hopf分支的存在性，但是并没有研究Hopf分支的性质。基于此，本文在文献[5]的基础上，进一步讨论系统Hopf分支的稳定性。

2 Hopf分支的存在性

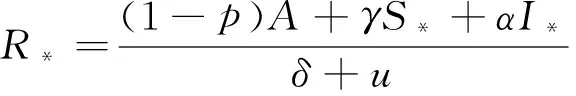
进而，文献[5]得到系统(1)在E(S*,I*,R*)处的特征方程。在此基础上得到系统(1)局部渐近稳定和产生Hopf分支的充分性条件。并确定得到产生Hopf分支的时滞临界点τ0的表达式：

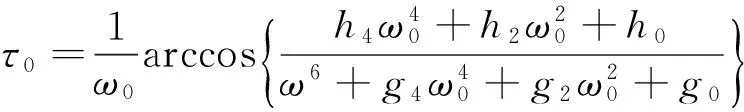
(2)

其中，g0,g2,g4,h0,h2,h4的表达式可由系统(1)中的各参数得到。即，当τ=τ0时，系统(1)在E(S*,I*,R*)处的特征方程具有一对共轭纯虚根±iω0(ω0>0).

3 分支周期解的稳定性

做转换t→(t/τ),u1(t)=S(t)-S*,u2(t)=I(t)-I*,u3(t)=R(t)-R*,τ=τ0+μ,μ∈R. 则μ=0是系统(1)产生Hopf分支的临界点，并且系统(1)可以转化为下列形式

(3)

其中，

ut=(u1(t),u2(t),u3(t))T∈

C=C([-1,0],R3)

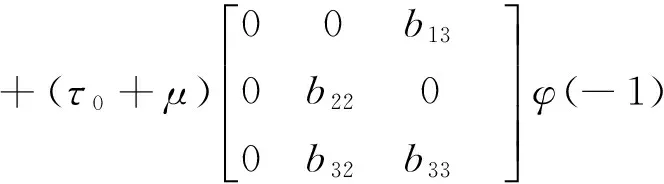
(4)

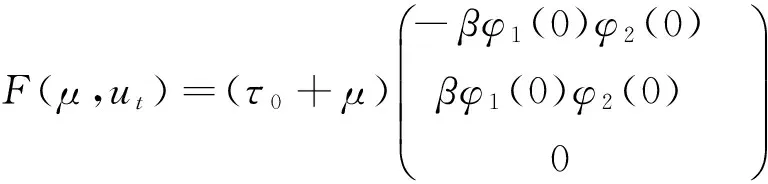
(5)

根据Riesz表示定理可知，存在有界变差函数η(θ,μ),θ∈[-1,0]使得

(6)

可以选取

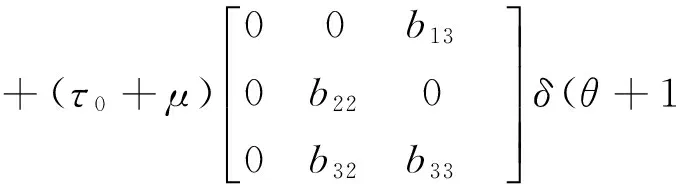
(7)

对于φ∈C([-1,0]),R3)，定义

(8)

和

(9)

则系统(3)可以转化为下列算子方程形式

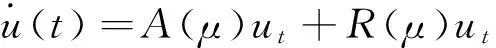
(10)

对于φ∈C1([-1,0]),(R3)*)，定义A(0)的伴随算子A*

(11)

以及双线性内积

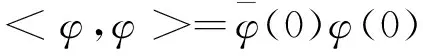
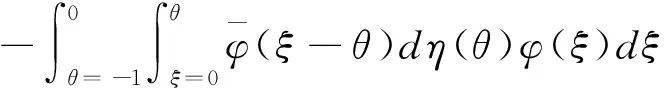
(12)

其中η(θ)=η(θ,0).

根据A(0)和A*的定义，可以计算得到A(0)的对应于+iω0τ0的特征向量ρ(θ)和A*的对应于-iω0τ0的特征向量ρ*(θ),

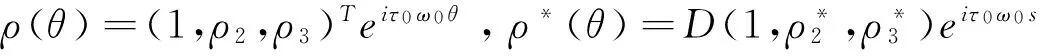
其中，

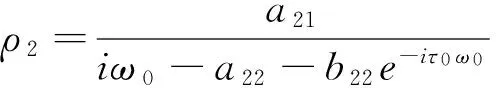
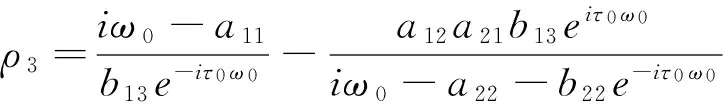
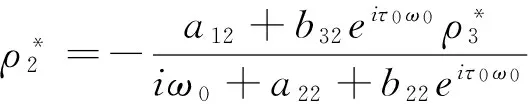
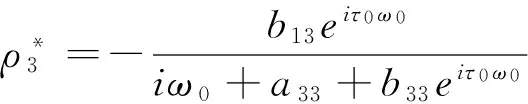
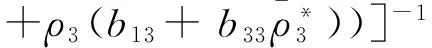
进而，利用文献[8]中的算法可以得到下列参数表达式：

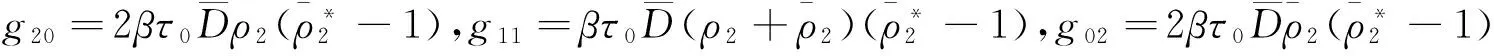
其中，

+E1e2iτ0ω0θ,

(13)

(14)

E1和E2的表达式可以由下列方程得到

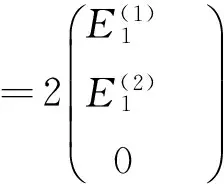
(15)

(16)

其中，

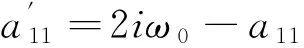
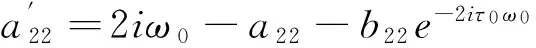
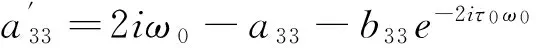
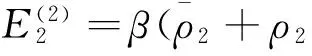
最后，可以得到下列表达式：

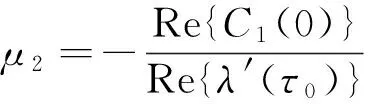
β2=2Re{C1(0)},

(17)

对于系统 (1), 如果μ2>0(μ2<0) , 则Hopf分岔是超临界(次临界)的；如果β2<0(β2>0),则分岔周期解是稳定(不稳定)的；如果T2>0(T2<0), 则分岔周期解的周期是递增(递减)的。

4 数值仿真

取文献[7]中相同的参数，得到如下系统(1)的示例模型：

(18)

经过计算得到系统(18)的正平衡点E(0.75,1.794,0.7885).进而得到ω0=0.6545,τ0=1.8672。当我们取τ=1.25∈[0,τ0)时，系统(18)是渐近稳定的。而当τ=1.965>τ0时，系统(18)失去稳定性，产生Hopf分支。仿真效果如图1-2所示。另外，根据公式(17)经过计算，可得μ2=0.6589>0，β2=-0.7686<0,T2=1.0126>0.因此，可知，系统(18)在τ0=1.8672处产生的Hopf分支是超临界的，分支周期解是稳定的并且周期是递增的。

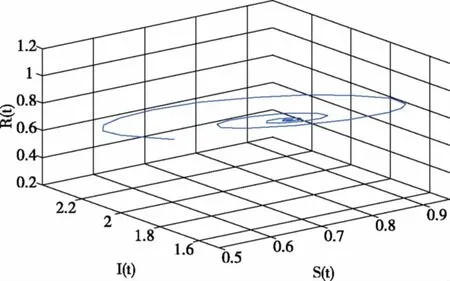
图1 当τ=1.25<τ0时，系统(18)渐近稳定Fig.1 System (18) is asymptotically stability when τ=1.25<τ0

图2 当τ=1.98>τ0时，系统(18)不稳定并 发生Hopf分支Fig.2 System (18) lose stability and a Hopf bifurcation occurs when τ=1.98>τ0

5 结论

本文在文献[7]的基础上，进一步研究了时滞SIRS计算机网络病毒传播模型的动力学性质。主要结果如下：利用中心流形定理和规范型理论，得到了确定Hopf分支的方向、稳定性和分支周期解周期大小的显性计算公式。从仿真结果来看，在一定条件下，模型(1)中三种状态的计算机数量会以周期震荡形式共存。因此，应该尽可能地延迟或控制Hopf分支的产生。本文所得结果是对文献[7]的重要补充。

[1]Yuan H, Chen G, Network virus-epidemic model with the point-to-group information propagation[J]. Applied Mathematics and Computation, 2008, 206(1):357-367.

[2]Gan C, Yang X, Liu W, Zhang X, An epidemicmodel of computer viruses with vaccination and generalized nonlinear incidence rate[J]. Applied Mathematics and Computation, 2013, 222(5): 265 -274.

[3]叶晓梦，杨小帆.基于两阶段免疫接种的SIRS计算机病毒传播模型[J].计算机应用，2013, 33(3): 739-742.

[4]冯丽萍，王鸿斌，冯素琴.基于生物学原理的计算机网络病毒传播模型[J].计算机工程，2011,37(11):155-157.

[5]Dong T, Liao X F, Li H Q, Stability and Hopf bifurcation in a computer virus model with multistate antivirus [J]. Abstract and Applied Analysis,2012,1(1):1-16.

[6]Feng L. P, Liao X F Li H Q, Hopf bifurcation analysis of a delayed viral infection model in computer networks[J]. Mathematical and Computer Modelling, 2012, 56(8):167-179.

[7]易飞.一类计算机网络病毒模型的稳定性[J].广东石油化工学院学报，2015,25(1):37-40.

[8]Hassard B D, Kazarinoff N D, Wan Y H, Theory and Applications of Hopf Bifurcation [M]. Cambridge University Press, Cambridge, 1981.

Periodic solutions of a delayed model for computer virus in network

ZHANG Zi-zhen ,XIE Wei-jie, JIANG Yue, LI Jia-qian, ZHAO Tao

(School of Management Science and Engineering, Anhui University of Finance and Economics, Anhui Bengbu 233030，China)

A delayed model for computer virus in network is investigated in this paper. The critical value when a Hopf bifurcation occurs is determined. Then, explicit formulas for direction and stability of the Hopf bifurcation and period of the periodic solution are obtained by using the center manifold theorem and the normal form theory. Finally, numerical simulations are presented in order to verify the obtained results.

SIRS model; Computer virus in network; Periodic solutions

2016-09-04

2016年度安徽省自然科学基金青年项目：“基于网络层析成像的Ad Hoc网络测量模型与方法研究”(项目编号：1608085QF145)；“具有分级感染率的时滞网络病毒传播模型动力学性质研究”(项目编号 ：1608085QF151)。

张子振(1982-)，男，山东聊城人,讲师、博士。主要研究方向：信息安全。

TP391.4

A

1673-6125(2016)04-0017-04