中考课题学习型试题

文/邓革周

中考课题学习型试题

文/邓革周

课题学习型试题，通常以探索、研究、实验操作等形式呈现在中考数学试题中.它以几何图形为题材，或以数学问题为背景，通过对有关问题的描述或逐步观察、操作、归纳、探究，进而发现问题，解决问题.试题结构通常分三部分，即阅读与理解、归纳与发现、运用与推广.解这类问题要理解范例所介绍的方法，并能够灵活进行迁移.

一、类比探究型

例1（2015年随州卷）问题：如图1，点E、F分别在正方形ABCD的边BC、CD上，∠EAF=45°，试判断BE、EF、FD之间的数量关系.

【发现证明】小聪把△ABE绕点A逆时针旋转90°至△ADG，从而发现EF=BE+FD，请你利用图1证明上述结论.

【类比引申】如图2，四边形ABCD中，∠BAD≠90°，AB=AD，∠B+∠D=180°，点E、F分别在边BC、CD上，则当∠EAF与∠BAD满足_____关系时，仍有EF=BE+FD.

【探究应用】如图3，在某公园的同一水平面上，四条通道围成四边形ABCD，已知AB=AD= 80米，∠B=60°，∠ADC=120°，∠BAD=150°，道路BC、CD上分别有景点E、F，且AE⊥AD，DF= 40（-1）米，现要在E、F之间修一条笔直的道路，求这条道路EF的长（结果取整数，参考数据：=1.41，=1.73）.

解析：【发现证明】如图1，∵△ADG≅△ABE，

∴AG=AE，∠DAG=∠BAE，DG=BE，

又∵∠EAF=45°，∴∠DAF+∠BAE=∠EAF=45°，

图1　

图2

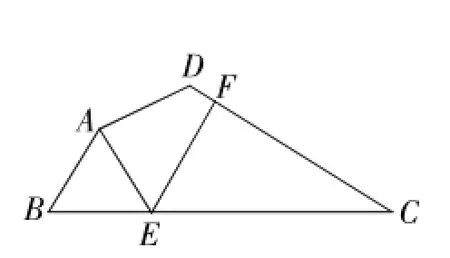
图3

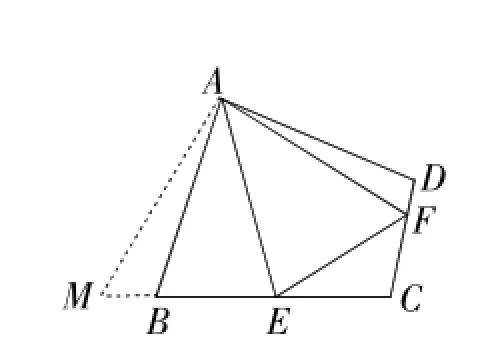
图4

图5

∴∠GAF=∠FAE，

在△GAF和△FAE中，

∴△AFG≌△AFE，

∴GF=EF，

又∵DG=BE，∴GF=BE+DF，

∴BE+DF=EF.

【类比引申】∠BAD=2∠EAF.理由如下：

如图4，延长CB至M，使BM=DF，连接AM，

∵∠ABC+∠D=180°，∠ABC+∠ABM=180°，

∴∠D=∠ABM，

在△ABM和△ADF中，

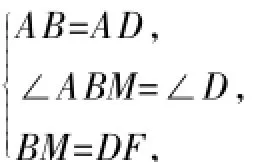
∴△ABM≅△ADF，

∴AF=AM，∠DAF=∠BAM，

∵∠BAD=2∠EAF，

∴∠DAF+∠BAE=∠EAF，

∴∠EAB+∠BAM=∠EAM=∠EAF，

在△FAE和△MAE中，

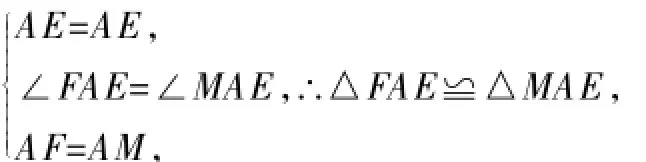
∴EF=EM=BE+BM=BE+DF，即EF=BE+DF.

故答案是：∠BAD=2∠EAF.

【探究应用】如图5，连接AF，延长BA、CD交于点G.

由四边形的内角和为360°，可得∠C=30°，从而∠G=90°.

在Rt△AGD中，∠GDA=60°，∠GAD=30°，AD=80，

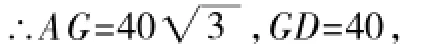
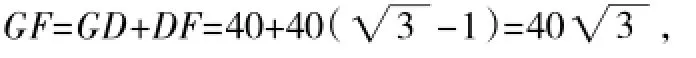
在Rt△GAF中，∵GA=GF，

∴∠GAF=45°，∴∠DAF=45°-30°=15°，

∴∠EAF=90°-15°=75°，∴∠BAD=2∠EAF，

在△BAE中，∠BAE=∠BAD-∠EAD=150°-90°=60°=∠B，

∴BE=AB=80，

由［类比引申］的结论可得

即这条道路EF的长约为109米.

温馨小提示：对于这类问题，发现证明、类比引申所蕴含的数学思想，往往是为拓展应用中的问题解决做铺垫的，我们要灵活运用.另外，对于图形的旋转或平移、折叠类问题，要充分利用变换后图形的形状、大小、对应线段、对应角相等的性质解题.

二、拓展应用型

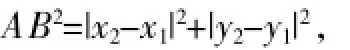
我们知道，圆可以看成到圆心的距离等于半径的点的集合，如图7所示，在平面直角坐标系xoy中，A（x，y）为圆上任意一点，则A到原点的距离的平方为OA2=|x-0|2+|y-0|2，当⊙O的半径为r时，⊙O的方程可写为：x2+y2=r2.

问题拓展：如果圆心坐标为P（a，b），半径为r，那么⊙P的方程可以写为______.

（1）证明AB是⊙P的切线；

（2）是否存在到四点O，P，A，B距离都相等的点Q？若存在，求Q点坐标，并写出以Q为圆心，以OQ为半径的⊙Q的方程；若不存在，说明理由.

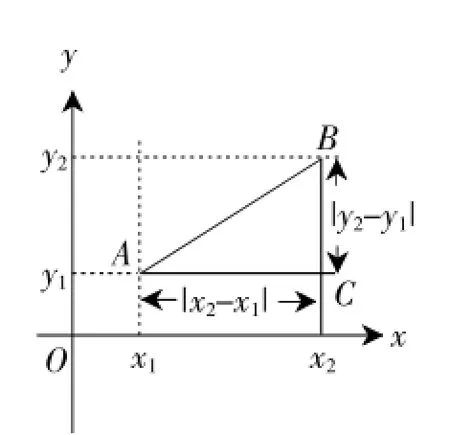
图6

图7

图8

解析：问题拓展：设A（x，y）为⊙P上任意一点，

∵P（a，b），半径为r，

故答案为（x-a）2+（y-b）2=r2.

综合应用：

（1）如图8，∵PO=PA，PD⊥OA，

∴∠OPD=∠APD，

在△POB和△PAB中，

∴△POB≅△PAB，∴∠POB=∠PAB，

∵⊙P与x轴相切于原点O，∴∠POB=90°，

∴∠PAB=90°，

∴AB是⊙P的切线.

（2）存在到四点O，P，A，B距离都相等的点Q.如图9，当点Q是线段BP的中点时，

∵∠POB=∠PAB=90°，

∴QO=QP=BQ=AQ.

此时点Q到四点O，P，A，B的距离都相等.

∵∠POB=90°，OA⊥PB，

∴∠OBP=90°-∠DOB=∠POA，

图9

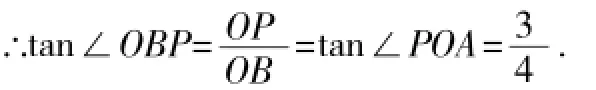
∵P点坐标为（0，6），

过点Q作QH⊥OB于H，

则有QH∥PO，∴△BHQ～△BOP，

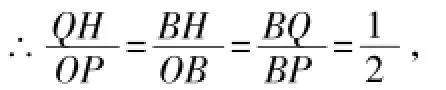
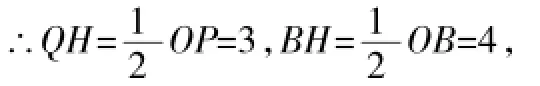
∴OH=8-4=4，

∴点Q的坐标为（4，3）.

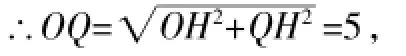
∴以Q为圆心，以OQ为半径的⊙Q的方程为（x-4）2+（y-3）2=25.

温馨小提示：对于这类问题，不要被材料中的“陌生面孔”所吓倒，要将新知识、新方法进行迁移，解决题目中提出的问题.