量体裁衣求概率
文/房延华
量体裁衣求概率
文/房延华

求概率需要分析不确定事件可能出现或发生的结果.若能根据题目的特点合理选择计算概率的方法,可使解题过程简捷明快,还能提高准确率.
1.一次操作问题,直接用公式P(A)=求概率

图1
例1(2015年烟台卷)如图1,有四张不透明卡片,除正面的函数关系式不同外,其余相同,将它们背面朝上洗匀后,从中抽取一张卡片,则抽到函数图像不经过第四象限的卡片的概率为_____.
∵4张卡片中只有y=x-1的图像经过第四象限,
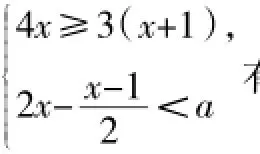
∴满足条件a的值为6,7,8,9,
温馨小提示:为了体现数学知识之间的相互联系,中考试题往往将多个知识点进行叠加,从而使问题具有较强的综合性.
2.事件涉及两个因素,并且抽取后不放回或一次抽取两个,用树状图法求概率

图2
例3(2015年徐州卷)小明参加某网店的“翻牌抽奖”活动,如图2,4张牌分别对应价值5,10,15,20(单位:元)的4件奖品.
(1)如果随机翻1张牌,那么抽中20元奖品的概率为_____;
(2)如果随机翻2张牌,且第一次翻过的牌不再参加下次翻牌,则所获奖品总值不低于30元的概率为多少?
(2)树状图如图3所示,
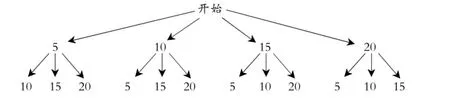
图3
∵所获奖品总值不低于30元有4种情况:30元、35元、30元、35元,
温馨小提示:对于一个事件,采用画树状图把所有可能的结果一一列出,既直观又条理分明,还可以避免重复和遗漏.
3.当事件涉及两个因素,并且出现的结果数目较多时,用列表法求概率
例4(2015年陕西卷)某中学要在全校学生中举办“中国梦·我的梦”主题演讲比赛,要求每班选一名代表参赛.九年级(1)班经过投票初选,小亮和小丽票数并列班级第一,现在他们都想代表本班参赛.经班长与他们协商决定,用他们学过的掷骰子游戏来确定谁去参赛(胜者参赛).
规则如下:两人同时随机各掷一枚完全相同且质地均匀的骰子一次,向上一面的点数都是奇数,则小亮胜;向上一面的点数都是偶数,则小丽胜;否则,视为平局,若为平局,继续上述游戏,直至分出胜负为止.
如果小亮和小丽按上述规则各掷一次骰子,那么请你解答下列问题:
(1)小亮掷得向上一面的点数为奇数的概率是多少?
(2)该游戏是否公平?请用列表或树状图等方法说明理由.(骰子:六个面上分别刻有1,2,3,4,5,6个小圆点的小正方体)
解:(1)∵向上一面的点数为奇数有3种情况,
(2)利用列表法得出所有可能的结果如下:
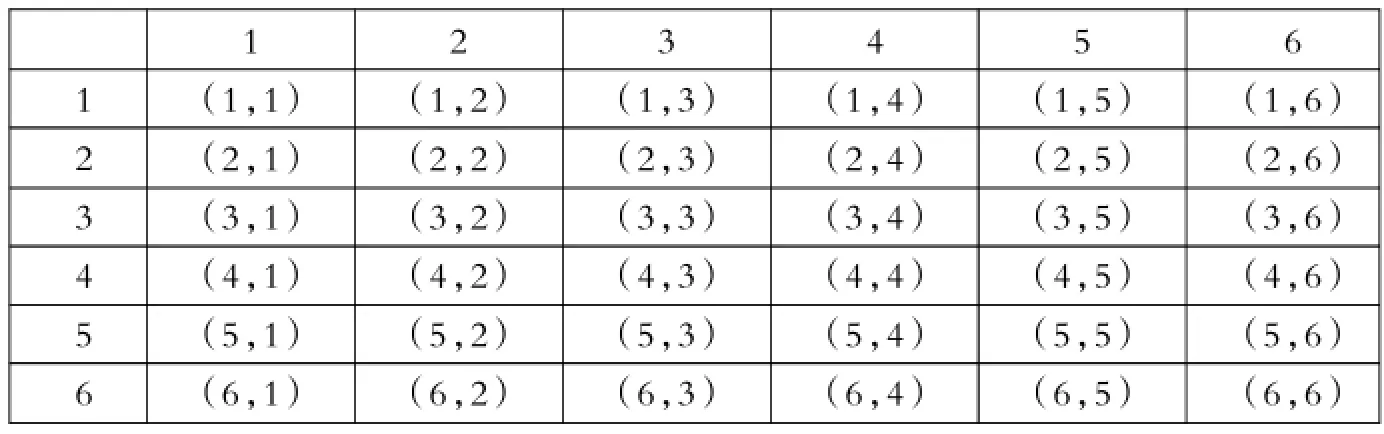
1 2 3 4 5 6 ___1 ___2 3 4 5 6 (1,1)(2,1)(3,1)(4,1)(5,1)(6,1)(1,2)(2,2)(3,2)(4,2)(5,2)(6,2)(1,3)(2,3)(3,3)(4,3)(5,3)(6,3)(1,4)(2,4)(3,4)(4,4)(5,4)(6,4)(1,5)__ __ (2,5)__ __ (3,5)(4,5)(5,5)(6,5)(1,6)(2,6)(3,6)(4,6)(5,6)(6,6)
由表可知,所有可能的结果共36种,其中小亮、小丽获胜各有9种结果,
∴游戏是公平的.
温馨小提示:判断游戏的公平性就要计算每个事件的概率,概率相等就公平,否则就不公平.
4.当事件涉及3个或更多的因素时,用树状图法求概率
例5(2015年聊城卷)在阳光体育活动时间,小亮、小莹、小芳和大刚到学校乒乓球室打乒乓球,当时只有一副空球桌,他们只能选两人打第一场.
(1)如果确定小亮打第一场,再从其余三人中随机选取一人打第一场,求恰好选中大刚的概率;
(2)如果确定小亮做裁判,用“手心、手背”的方法决定其余三人哪两人打第一场.游戏规则是:三人同时伸“手心、手背”中的一种手势,如果恰好有两人伸出的手势相同,那么这两人上场,否则重新开始,这三人伸出“手心”或“手背”都是随机的,请用画树状图的方法求小莹和小芳打第一场的概率.
解:(1)∵小亮打第一场,再从小莹、小芳和大刚中随机选取一人打第一场有三种情况,
(2)画树状图,如图4所示.

图4
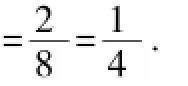
温馨小提示:本题有三次操作,对于两步以上随机事件问题,应选用树状图法求概率.
5.枚举法——求二次事件概率问题的利器
例6(2015年德州卷)经过某十字路口的汽车,可能直行,也可能左转或者右转.如果这三种可能性大小相同,则经过这个十字路口的两辆汽车一辆左转,一辆右转的概率是().
解:两辆汽车走的方向共有9种可能性:(直,直),(直,左),(直,右),(左,直),(左,左),(左,右),(右,直),(右,左),(右,右),其中一左一右的可能性有两种,
温馨小提示:枚举法是确定概率的常用方法,是解决二次事件概率的利器.
6.利用面积比求几何型概率
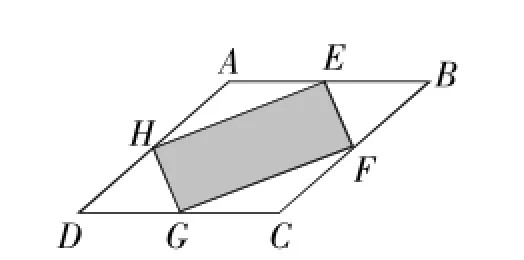
图5
例7(2015年呼和浩特卷)如图5,四边形ABCD是菱形,E、F、G、H分别是各边的中点,随机地向菱形ABCD内掷一粒米,则米粒落到阴影区域内的概率是______.
解:∵四边形ABCD是菱形,E、F、G、H分别是各边的中点,
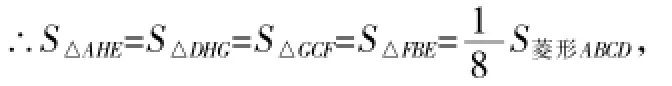
温馨小提示:解题的关键是确定有效面积与整体面积,并求出它们的比值.这是求几何型概率的常用方法.

