尺规作图题新走向
文/朱广科
尺规作图题新走向
文/朱广科
近几年中考作图题,已不局限于对基本作图技能的考查,一些设计新颖、富有创意的作图题越来越受到命题者青睐.情景型、设计型、阅读理解型、开放型等题型层出不穷.这些作图题大都联系生活实际,需要进行多方位、多角度、多层次探索,以检验我们思维的灵活性、发散性、创新性.现以2015年的中考试题为例,就各种作图题分类说明,供你复习时参考.
一、基本作图型
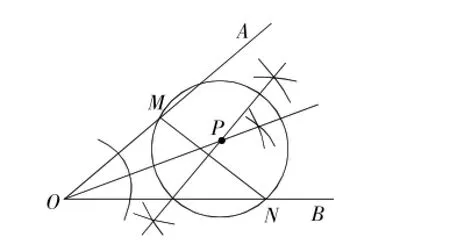
图1
例1(2015年兰州卷)如图1,在图中求作⊙P,使⊙P满足以线段MN为弦且圆心P到∠AOB两边的距离相等.(要求:尺规作图,不写作法,保留作图痕迹,并把作图痕迹用黑色签字笔加黑)
解:点P是∠AOB的平分线与线段MN的垂直平分线的交点,以P为圆心,PM为半径的圆为所求,如图1,⊙P就是所求作的圆.
点评:尺规作图是指用无刻度的直尺和圆规来作图,最基本、最常用的尺规作图,通常称为基本作图.解尺规作图题时,要明确直尺和圆规的功能,理解图形的本质特征,确定正确的作图顺序,一般需要保留作图痕迹.
二、图形剪拼型
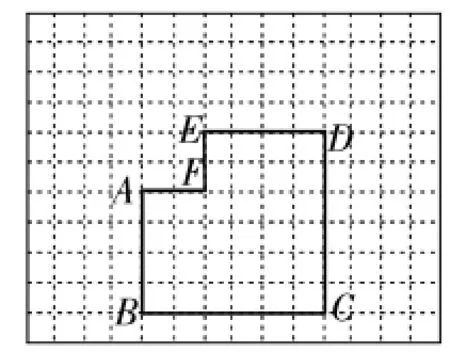
图2

图3

图4
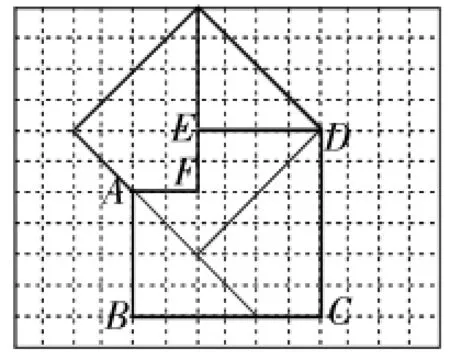
图5
例2(2015年龙岩卷)下列网格中的六边形ABCDEF是由边长为6的正方形左上角剪去边长为2的正方形所得,该六边形按一定的方法可剪拼成一个正方形.
(1)根据剪拼前后图形的面积关系求出拼成正方形的边长;
(2)如图3,把六边形ABCDEF沿EH,BG剪成①于③三部分,请在图4中画出将于③与①拼成的正方形,然后标出于③变动后的位置,并指出于③属于旋转、平移和轴对称中的哪一种变换;
(3)在图5中画出一种与图4不同位置的两条裁剪线,并在图5中画出将此六边形剪拼成的正方形.
解:(1)根据剪拼前后图形的面积相等,得出拼成的正方形的边长为
(2)如图4所示,于③都属于平移.
(3)如图5所示.
点评:有趣的剪拼问题常蕴含着理性的数学思考.本题以图形的剪拼为背景,考查了正方形、勾股定理等有关知识.理解旋转、平移和轴对称变换的特点,合理计算发现拼接前后图形中边、角、面积之间的关系,从而确定剪拼方案.
三、图形变换型
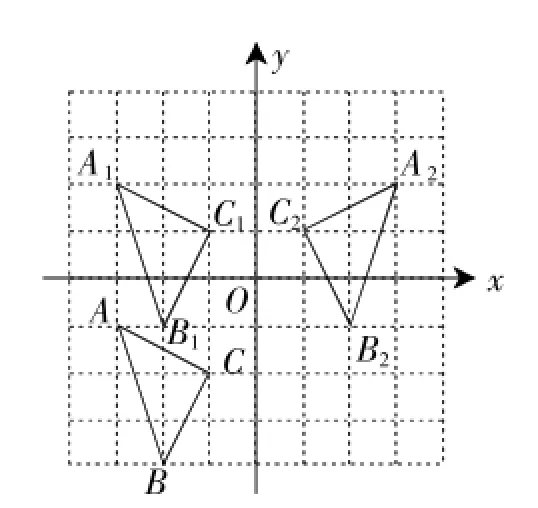
图6
例3(2015年聊城卷)在如图6所示的直角坐标系中,每个小方格都是边长为1的正方形,△ABC的顶点均在格点上,点A的坐标是(-3,-1).
(1)将△ABC沿y轴正方向平移3个单位得到△A1B1C1,画出△A1B1C1,并写出点B1坐标;
(2)画出△A1B1C1关于y轴对称的△A2B2C2,并写出点C2的坐标.
解:(1)如图6所示,△A1B1C1为所求;点B1坐标为(-2,-1).
(2)如图6所示,△A2B2C2为所求,点C2的坐标为(1,1).
点评:图形变换主要包括图形的平移、翻折、旋转等几种情况.解决本题的关键是学会观察并挖掘其中的变换条件,根据变换规律得出对应点位置.
四、开放探究型
例4(2015年南京卷)如图7,在边长为4的正方形ABCD中,请画出以A为一个顶点,另外两个顶点在正方形ABCD的边上,且含边长为3的所有大小不同的等腰三角形.(要求:只要画出示意图,并在所画等腰三角形长为3的边上标注数字3)
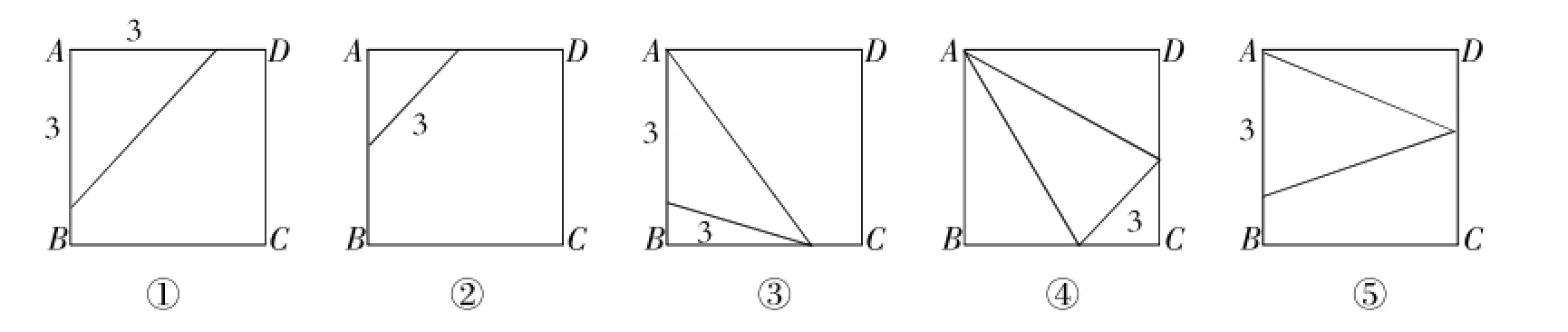
图7
解:满足条件的所有图形如图7所示.
点评:解此类问题需要分类讨论.对于结论不确定的问题,因解题思路不同及理解程度不同,将得到不同的结论,均可作为问题的答案.此题主要考查等腰三角形的判定,合理利用图形分类是解题的关键.分类讨论时,要慎密思考,做到不重不漏.
五、阅读理解型
例5(2014年宁波卷)在边长为1的小正方形组成的方格纸中,若多边形各顶点都在方格纸的格点(横竖格子线的交点)上,这样的多边形称为格点多边形.记格点多边形内的格点数为a,边界上的格点数为b,则格点多边形的面积可表示为S=ma+nb-1,其中m,n为常数.
(1)在下面的方格纸中各画一个面积为6的格点多边形,依次为三角形、平行四边形(非菱形)和菱形;
(2)利用(1)中的格点多边形确定m,n的值.
解:(1)如图8所示.
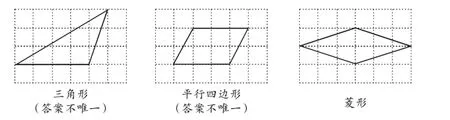
图8
(2)在图8的三角形中,a=4,b=6,S=6,
在平行四边形(非菱形)中,a=3,b=8,S=6,在菱形中,a=5,b=4,S=6,
任选两组代入S=ma+nb-1,
点评:依照材料给出的定义,对新问题进行类似的信息迁移,考查应用新知识的能力.要求我们在阅读的基础上,寻找规律并应用于解决新问题,理解格点多边形的面积公式S=ma+ nb-1,根据已知画出各多边形是解题的关键.
六、问题情景型
例6(2015年北京卷)在数学课上,老师提出如下问题:

小芸的作法如下:
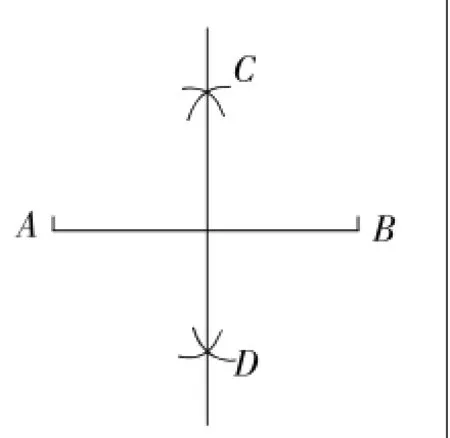
图8
如图8所示,
(2)作直线CD.
老师说:“小芸的作法正确.”
请回答:小芸的作图依据是____________________________________
解:∵CA=CB,DA=DB,
∴CD垂直平分AB(到线段两个端点的距离相等的点在线段的垂直平分线上).
故答案为:到线段两个端点的距离相等的点在线段的垂直平分线上.
点评:本题是通过师生对话的形式给出的一类作图题,试题活泼生动、趣味十足,激发学生解题的激情,在呈现方式上,不是直接尺规作图,而是给出作图的方法和过程,让学生找出作图的依据,其目的是考查学生搜索信息、整理信息和应用信息的能力,要求学生不仅要知其然,还要知其所以然.

