开放性问题专题分析

文/王锋

开放性问题专题分析

文/王锋

开放性问题是中考常见题型，侧重于考查考生的合情推理与演绎推理、发散思维能力.在中考中有以下常见题型.

一、条件开放型

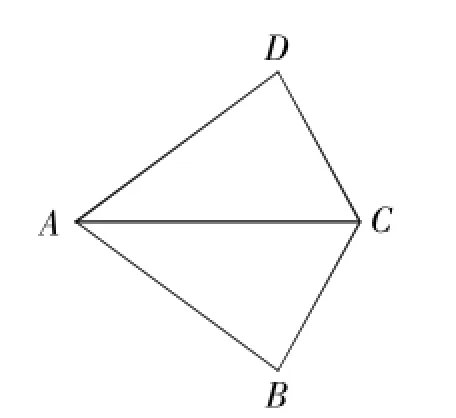
图1

例1（2015年盐城卷）如图1，在△ABC与△ADC中，已知AD= AB，在不添加任何辅助线的前提下，要使△ABC≅△ADC，只需要再添加一个条件可以是_____.

解析：由题设可知AD=AB，AC是△ABC与△ADC的公共边，要使△ABC≅△ADC，

①若根据“SAS”，需添加条件∠DAC=∠BAC；

于若根据“SSS”，需添加条件CD=CB；

③若根据“HL”，需添加条件∠ABC=∠ADC=90°等等.

∴填∠CAD=∠CAB或DC=BC或∠B=∠D=90°.

评点：添加条件使得两个三角形全等（或相似），或使四边形为某种特殊的四边形是条件开放型中最常见的问题之一，既要注意已知条件，更要挖掘题目或图形中隐含的条件，切忌添加一些重复的或无效的条件.

二、添加运算过程型

例2（2014年滨州卷）写出一个运算结果是a6的算式______.

解：答案不唯一.可填a2·a4或a·a5或（a3）2.

评点：熟悉运算法则，即可正解求解.

三、结论开放型

评点：满足题设条件的结论可能有无数多个，按要求选择一个或几个即可.

四、作图开放型

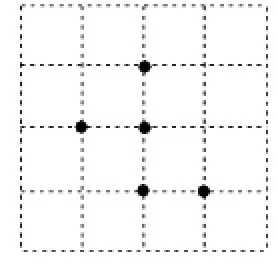
图2

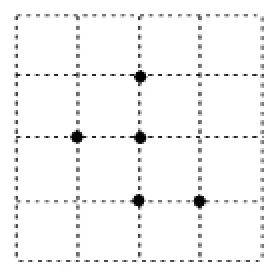
图3

例5图2、图3都是4×4的正方形网格，每个小正方形的顶点称为格点，每个小正方形的边长均为1.在每个网格中标注了5个格点.按下列要求画图：

（1）画一个以格点为顶点的等腰三角形，使其内部只有3个已标注的格点；

（2）以格点为顶点，画一个正方形，使其内部只有3个已标注的格点，且边长为无理数.

解析：本题属于开放性作图问题（有部分限制条件），答案不唯一，可任选一个.

（1）根据标注的5个点的位置，通过简单计算（利用勾股定理求边长）可得4种作图方案，如图4所示.

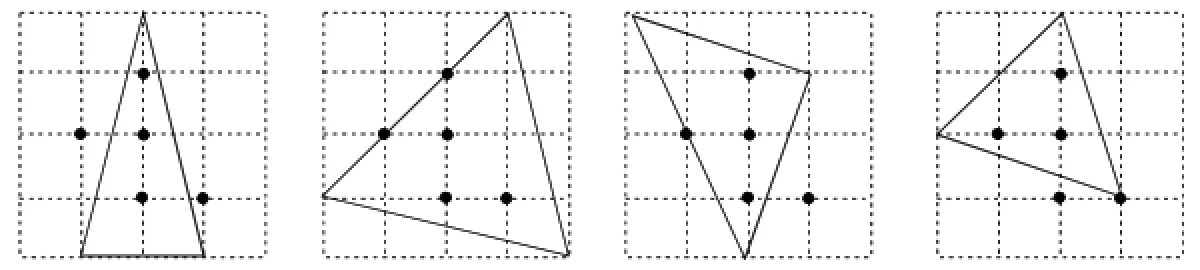
图4

（2）根据标注的5个点的位置，通过简单计算（利用勾股定理求边长）可得4种作图方案，如图5所示.

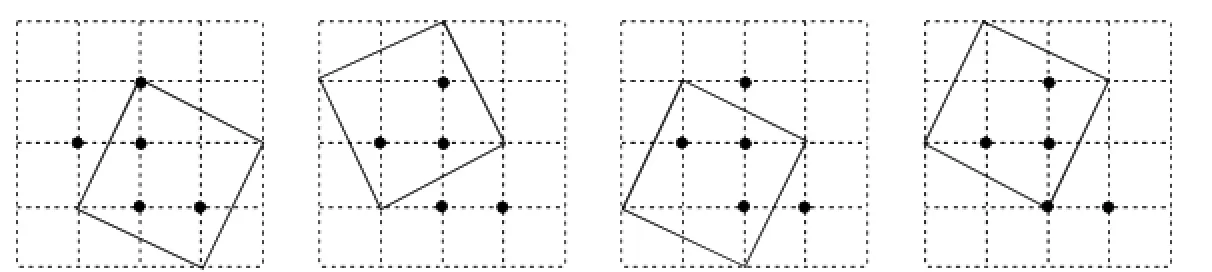
图5

评点：利用正方形网格设计几何图形是中考的热点问题，解答此类问题需利用网格的结构特征——每个网格的边长可以看作一个单位长度；水平网格线互相平行，竖直网格线互相平行；水平网格线与竖直网格线互相垂直；利用正方形网格的对角线可以得到45°、90°、135°的特殊角等.另外，要充分发挥勾股定理的作用，发现一些特殊的三角形、四边形及全等（或相似）三角形，从而为解决有关问题提供条件.

五、评价开放型

例6（2014年荆门卷）我市某中学七、八年级各选派10名选手参加学校举办的“爱我荆门”知识竞赛，计分采用10分制，选手得分均为整数，成绩达到6分或6分以上为合格，达到9分或10分为优秀.这次竞赛后，七、八年级两支代表队选手成绩分布的条形统计图和成绩统计分析表如图6所示，其中七年级代表队得6分、10分的选手人数分别为a，b.

（1）请依据图表中的数据，求a，b的值；

（2）直接写出表中m，n的值；

（3）有人说七年级队的合格率、优秀率均高于八年级队，所以七年级队的成绩比八年级队好，但也有人说八年级队的成绩比七年级队好.请你给出两条支持八年级队成绩好的理由.

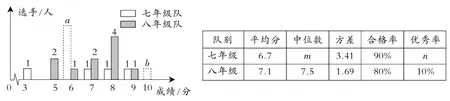
图6

解析：（1）由七年级参赛人数10人，得1+a+1+1+1+b=10，即a+b=6；由平均分为6.7，得（3×1+6a+7×1+8×1+9×1+10b）=6.7，即6a+10b=40，联立a+b=6，解得a=5，b=1.

（3）八年级队的成绩比七年级队好的理由有三条，可以从中任意选两条.

从平均分看，八年级队的平均分：1_（5×2+6×1+7×2+8×4+9×1）=7.1分，七年级队的10平均分：1_（3+6×5+7+8+9+10）=6.7分，八年级队的成绩比七年级队的高. 10

从中位数看，七年级队的中位数是6.5，八年级队的是7.5，八年级队成绩的中位数比七年级队的高.

评点：运用“三数”“两差”对某个对象进行评价是统计中常考的问题之一，对于同个对象，从某个角度去评价时可能是“较差的”，从另一个角度去评价时，也许变成是“较好的”.

六、取值开放型

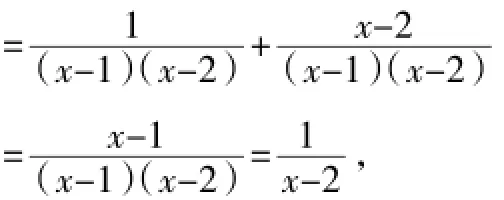
另外，也可选x=-2代入求值.

评点：在分式（或根式）的化简求值中，字母取值经常是开放性的，选取的数既要保证化简后的结果有意义，又要保证原分式（或根式）有意义.