中考函数应用题
文/肖新平
中考函数应用题
文/肖新平

函数是初中数学的核心内容,它包括一次函数、反比例函数、二次函数.在中考命题中,函数应用题一直是命题的重点,其中利用函数的性质进行决策和最优化处理实际问题是中考命题的热点.
一、一次函数应用题

命题角度命题形式1.利用函数图像和性质,如增减性解决决策类问题,它常与不等式(组)一起考查;2.建立一次函数模型,利用一次函数图像特征来解决实际问题,它常与方程(组)一起考查.______________ 1.方案决策类问题;2.图像信息类问题.
1.方案决策类问题
例1(2015年广安卷)为了贯彻落实市委市政府提出的“精准扶贫”精神,某校特制定了一系列关于帮扶A,B两贫困村的计划.现决定从某地运送152箱鱼苗到A,B两村养殖,若用大、小货车共15辆,则恰好能一次性运完这批鱼苗,已知这两种大、小货车的载货能力分别为12箱/辆和8箱/辆,其运往A,B两村的运费如下表:

目的地车型大货车小货车A村(元/辆)800 400 B村(元/辆)900 600
(1)这15辆车中大、小货车各有多少辆?
(2)现安排其中10辆货车前往A村,其余货车前往B村,设前往A村的大货车为x辆,前往A,B两村总费用为y元,试求出y与x的函数解析式;
(3)在(2)的条件下,若运往A村的鱼苗不少于100箱,请你写出使总费用最少的货车调配方案,并求出最少费用.
解析:(1)设大货车有x辆,小货车有y辆,
∴大货车有8辆,小货车有7辆.
(2)y=800x+900(8-x)+400(10-x)+600[7-(10-x)]=100x+9400(3≤x≤8,且x为整数).
(3)由题意得12x+8(10-x)≥100,解得x≥5,
又∵3≤x≤8,
∴5≤x≤8且x为整数,
∵y=100x+9400,k=100>0,y随x的增大而增大,
∴当x=5时,y最小,
y的最小值为=100×5+9400=9900.
答:总运费最少的调配方案是5辆大货车、5辆小货车前往A村,3辆大货车、2辆小货车前往B村.最少运费为9900元.
温馨小提示:解这类题需建立一次函数并求出自变量的取值范围,根据一次函数的性质及自变量的范围或整数解来求最值,从而确定方案.

图1
2.图像信息类问题
例2(2015年徐州卷)为加强公民的节水意识,合理利用水资源,某市对居民用水实行阶梯水价,居民家庭每月用水量划分为三个阶梯,一、二、三级阶梯用水的单价之比等于1∶1.5∶2.如图1折线表示实行阶梯水价后每月水费y(元)与用水量xm3之间的函数关系.其中线段AB表示第二级阶梯时y与x之间的函数关系.
(1)写出点B的实际意义;
(2)求线段AB所在直线的表达式;
(3)某户5月份按照阶梯水价应缴水费102元,其用水量为多少立方米?
解析:(1)B点的实际意义:用水25m3,需缴水费90元.
(2)设第一阶梯用水的单价为x元/m3,则第二阶梯用水单价为1.5x元/m3,A(a,45),
∴A(15,45),B(25,90).
设线段AB所在直线的表达式为y=kx+b,
(3)设该户5月份用水量为xm3(x>90),由(2)知第二阶梯用水的单价为4.5元/m3,第三阶梯用水的单价为6元/m3.
根据题意得90+6(x-25)=102,解得x=27.
答:该用户5月份用水量为27m3.
温馨小提示:分段函数一般应从如下几方面入手:(1)寻找分段函数的分段点;(2)针对每一段函数关系,求出相应的函数解析式;(3)利用分段函数解答问题.
二、反比例函数应用题

命题角度 以反比例函数图像为背景,综合考查反比例函数的解析式的求法和反比例函数的性质.在同一坐标系中与一次函数(正比例函数)综合考查.命题形式
例3(2015年长沙卷)在直角坐标系中,我们不妨将横坐标、纵坐标均为整数的点称之为“中国结”.
(3)若二次函数y=(k2-3k+2)x2+(2k2-4k+1)x+k2-k(k为常数)图像与x轴相交得到两个不同的“中国结”,试问该函数图像与x轴所围成的图形中(含边界),一共包含多少个“中国结”?
解:(1)当x=0时,y=2,故点(0,2)是“中国结”.
∴当k=1时,“中国结”的坐标为(1,1)、(-1,-1);当k=-1时,“中国结”的坐标为(1,-1)、(-1,1).
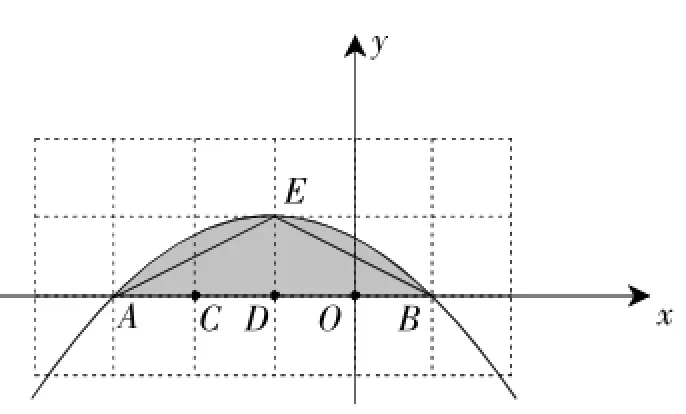
图2
(3)令y=0,得(k2-3k+2)x2+(2k2-4k+1)x+k2-k=0,
∵x1、x2都是整数,∴k=,此时,x1=-3,x2=1,
该函数图像如图2,符合条件的一共有6个“中国结”:(-3,0)、(-2,0)、(-1,0)、(0,0)、(1,0)、(-1,1)(即点A、B、C、D、E、O共6个点).
温馨小提示:弄懂有理数与无理数的概念是解题的关键.
三、二次函数应用题

命题角度命题形式1.利用二次函数表示实际问题中变量之间的关系,如桥洞等问题;2.利用二次函数解决实际问题中的最优化问题(如面积最值,线段最值,商品利润最值等),其实质求函数的最大值或最小值._________________________________________________________ 1.以实际生活中的抛物线模型为背景进行考查;2.以最值问题进行考查._______________________________________________
例4(2015年青岛卷)如图3,隧道的截面由抛物线和长方形构成,长方形的长是12m,宽是4m.按照图中所示的直角坐标系,抛物线可以用y=-x2+bx+c表示,且抛物线上的点C到墙面OB的水平距离为3m,到地面OA的距离为m.

图3
(1)求该抛物线的函数关系式,并计算出拱顶D到地面OA的距离;
(2)一辆货运汽车载一长方体集装箱后高为6m,宽为4m,如果隧道内设双向行车道,那么这辆货车能否安全通过?
(3)在抛物线型拱壁上需要安装两排灯,使它们离地面的高度相等.如果灯离地面的高度不超过8m,那么两排灯的水平距离最小是多少米?

∴拱顶D到地面OA的距离为10m.
(2)抛物线的顶点是(6,10),当x=6+4=10时,
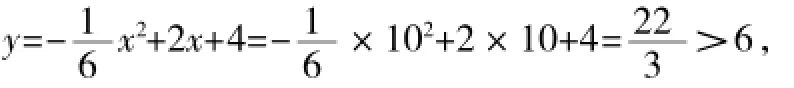
∴这辆货车能安全通过.
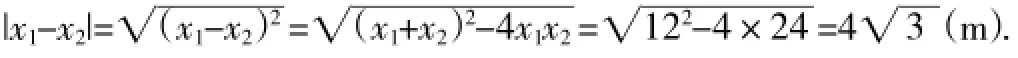
例5(2015年铁岭卷)某蔬菜经销商去蔬菜生产基地批发某种蔬菜,已知批发量在20千克~60千克之间(含20千克和60千克)时,每千克批发价是5元;若超过60千克时,批发的这种蔬菜全部打八折,但批发总金额不得少于300元.
(1)根据题意,填写下表:
∴两排灯水平距离的最小值是

蔬菜的批发量(千克)所付金额(元)……25 125 60 90 ……75 300

图4
(2)经调查,该蔬菜经销商销售该种蔬菜的日销售量y(千克)与零售价x(元/千克)是一次函数关系,其图像如图4,求出y与x之间的函数关系式;
(3)若该蔬菜经销商每日销售此种蔬菜不低于75千克,且当日零售价不变,那么零售价定为多少时,该经销商销售此种蔬菜的当日利润最大?最大利润为多少元?
解析:(1)当蔬菜批发量为60千克时,60× 5=300(元),
当蔬菜批发量为90千克时,90×5×0.8=360(元).故分别填300,360.

∴y=-30x+240.
(3)设当日可获利润w(元),当日零售价为x元,由(2)知,
w=(-30x+240)(x-5×0.8)=-30(x-6)2+120,
当x=6时,当日可获得利润最大,最大利润为120元.
温馨小提示:利用二次函数解决最优化问题,实际上就是求函数的最大值或最小值.建立二次函数关系式时,通常需要用到下列的等量关系:①每件利润=销售单价-销售成本;②总利润=总销售额-总成本=每件利润×销售量;③销售额=销售单价×销售量.

