规律探究题的求解策略

刘顿

规律探究题的求解策略

刘顿

规律探究型问题是指在一定条件下，探索数学对象所具有的规律性，它往往给出一组数、式子、图形或条件，要求考生通过阅读、观察、分析、猜想来探索规律.它体现了从特殊到一般的数学思想.

题型一　探究数的变化规律

例1（2015年孝感卷）观察下列等式：

1=12，1+3=22，1+3+5=32，1+3+5+7=42，…，则1+3+5+7+…+2015=_____.

解：∵1=12，1+3=22，1+3+5=32，1+3+5+7=42，…，

∴1+3+5+…+（2n-1）=n2，

由2n-1=2015，解得n=1008，

∴1+3+5+7+…+2015=10082=1 016 064.

填1 016 064.

说明：给出前面几个数据，要求这一组数据前n个数的和，考查考生对数据规律的探究能力，需要根据前面几个数的变化情况，发现一般规律，从而解决问题.

题型二　探究恒等式的变化规律

例3（2015年内江卷）（1）填空：（a-b）（a+b）=______；（a-b）（a2+ab+b2）=______；（a-b）（a3+a2b+ab2+b3）=______.

（2）猜想：（a-b）（an-1+an-2b+…+abn-2+bn-1）=_____（其中n为正整数，且n≥2）.

（3）利用（2）猜想的结论计算：29-28+27-…+23-22+2.

解：（1）∵（a-b）（a+b）=a2-b2，

（a-b）（a2+ab+b2）=a3+a2b+ab2-a2b-ab2-b3=a3-b3，

（a-b）（a3+a2b+ab2+b3）=a4+a3b+a2b2+ab3-a3b-a2b2-ab3-b4=a4-b4，

∴分别填上a2-b2，a3-b3，a4-b4.

（2）由（1）的规律得，原式=an-bn.

（3）29-28+27-…+23-22+2=（2-1）（28+26+24+22+2）=342.

说明：本题考查了多项式的乘法规律，发现规律是解题的关键.

题型三　探究图形的变化规律

图1

例4（2015年益阳卷）图1是用长度相等的小棒按一定规律摆成的一组图案，第1个图案中有6根小棒，第2个图案中有11根小棒……则第n个图案中有______根小棒.

解：第（1）个图案有6根小棒，第（2）个图案比第（1）个图案多5根小棒，在接下来的图案中，都依次增加5根小棒.因此有：

第（1）个图案有6根小棒，第（2）个图案有（6+5）根小棒，第（3）个图案有（6+5+5）根小棒，第（4）个图案有（6+5+5+5）根小棒……第（n）个图案中有6+5（n-1）=5n+1根小棒.

答案为5n+1.

说明：观察简单、特殊图形，发现数量规律，再推广到一般情况，从而得到答案.

题型四　探究周期性变化规律

图2

例5（2015年邵阳券）如图2，在矩形ABCD中，已知AB=4，BC=3，矩形在直线l上绕其右下角的顶点B向右旋转90°至图①位置，再绕右下角的顶点继续向右旋转90°至图于位置，依次类推，这样连续旋转2015次后，顶点A在整个旋转过程中所经过的路程之和是（）.

A.2015πB.3019.5πC.3018πD.3024π

图3

说明：探索图形周期性变化，通常需要观察图形变化的特点，发现这些变化的内在联系，从而解决问题.

题型五　探究坐标的变化规律

例6（2015年济南卷）在平面直角坐标系中有三个点A（1，-1）、B（-1、-1）、C（0，1），点P （0，2）关于A的对称点为P1，P1关于B的对称点为P2，P2关于C的对称点为P3，按此规律继续以A、B、C为对称中心重复前面的操作，从而得到P4、P5、P6……则点P2015的坐标是（）.

A.（0，0）B.（0，2）

C.（2，-4）D.（-4，2）

解：如图4，P（0，2），第1次变换后P1（2，-4），第2次变换后P2（-4，2），第3次变换后P3（4，0），第4次变换后P4（-2，-2），第5次变换后P5（0，0），第6次变换后P6（0，2），从而可知每6次一循环，而2015÷6= 335……5，

图4

∴点P2015的坐标是（0，0）.选A.

说明：解坐标规律探索题，要发挥数形结合的作用，从特例出发，经历实验操作、观察分析、归纳猜想得出一般性的结论，从而得到问题的答案.

题型六　探究长度的变化规律

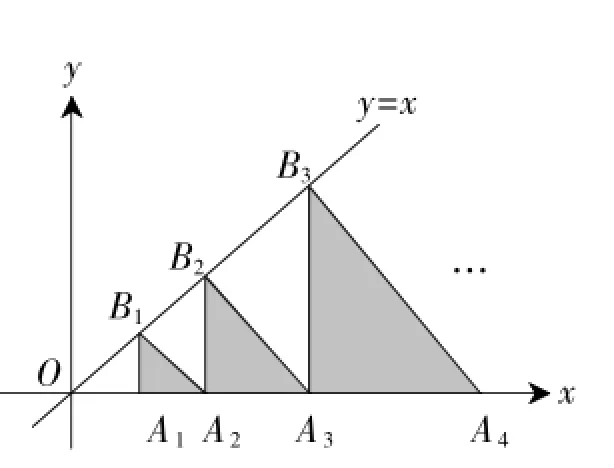
图5

例 7（2015年衡阳卷）如图5，△A1B1A2，△A2B2A3，△A3B3A4，…，△AnBnAn+1都是等腰直角三角形，其中点A1，A2，…，An在x轴上，点B1，B2，…，Bn在直线y=x上.已知OA1=1，则OA2015的长为_____.

解：∵OA1=1，∴点A1坐标为（1，0），

又∵△A1B1A2为等腰直角三角形，

∴B1A1⊥x轴，

∵点B1在直线y=x上，

∴点B1的坐标为（1，1），且B1A1=A1A2=1，

∴A2的坐标为（2，0），即OA2=2=21，

同理可得，点A3的坐标为（4，0），即OA3=4=22，

如此类推，可得到OA4=8=23，OA5=16=24，…，

∴OA2015=22014.填22014.

说明：从简单图形出发，通过归纳，猜想，得出一般性结论.

题型七　探究面积的变化规律

例8（2015年盐城卷）设△ABC的面积为1，如图6将边BC、AC分别2等份，BE1、AD1相交于点O，△AOB的面积记为S1；如图7将边BC、AC分别3等份，BE1、AD1相交于点O，△AOB的面积记为S2……以此类推，则Sn可表示为______.（用含n的代数式表示，其中n为正整数）

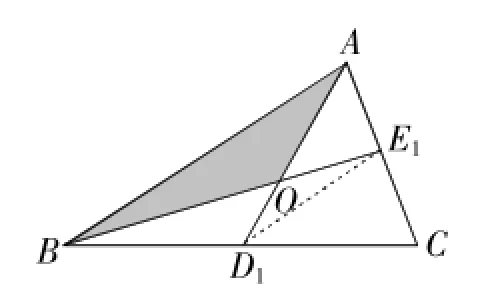
图6

图7

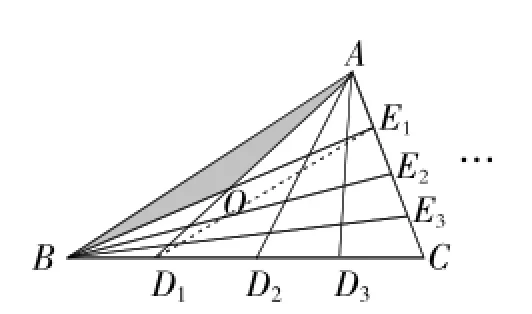
图8

解：如图6，连接D1E1，由三角形中位线定理，得AB=2D1E1，D1E1∥AB，

∴△OD1E1～△OAB，

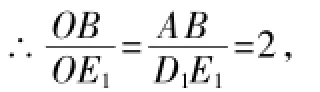
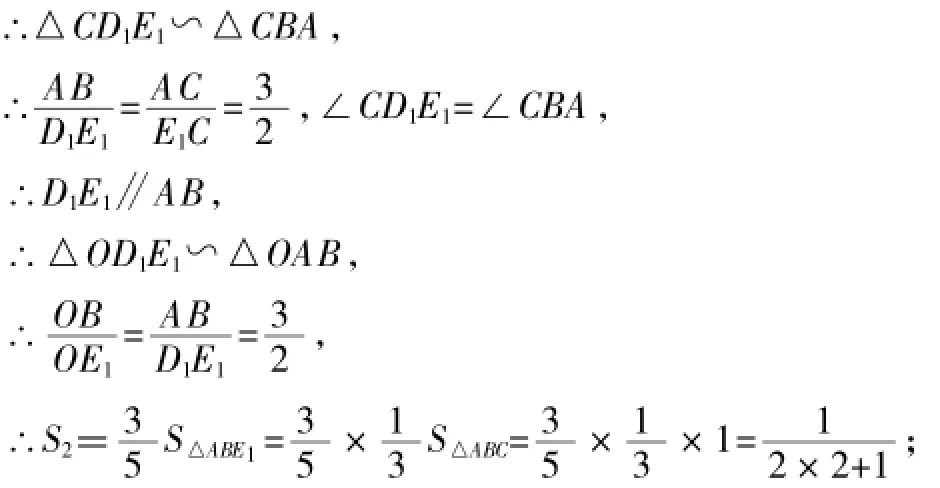
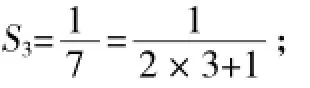
说明：求出简单图形的面积，观察各图形之间的联系，找出面积的变化规律，从而求出第n个图形的面积.

题型八　探究操作问题的变化规律

例9（2015年铁岭卷）如图9，将一条长度为1的线段三等分，然后取走其中的一份，称为第一次操作；再将余下的每一条线段三等分，然后取走其中的一份，称为第二次操作……如此重复操作，当第n次操作结束时，被取走的所有线段长度之和为_____.

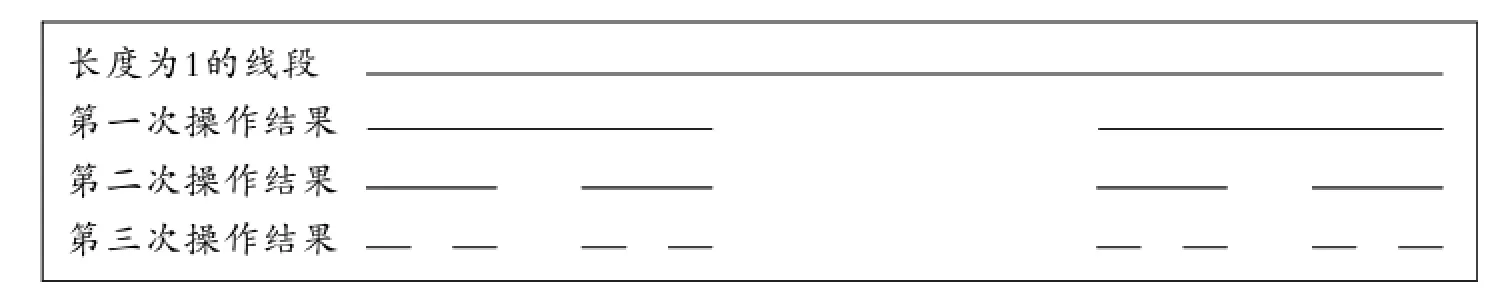
图9

说明：若不理解题意，操作就无法进行，从而找不到被取走线段长度和的规律而难以求解.