琴生不等式的类别与运用
浙江省宁波市北仑明港中学 (315806)
甘大旺
琴生不等式的类别与运用
浙江省宁波市北仑明港中学(315806)
甘大旺
琴生(Jensen,1859 ~ 1925)在丹麦的纳克斯考出生,跟随做地产经理的父亲在瑞典度过大部分童年时光,17岁考进瑞典的哥本哈根科技学院,没有拿到大学文凭就跟随父母返回了丹麦,随后自学数学,22岁至65岁在电话公司从事技术工作,是一位成功的电讯工程师.琴生利用业余时间钻研数学,其中流传至今的研究成果是以凹凸函数为基础的“琴生不等式”.
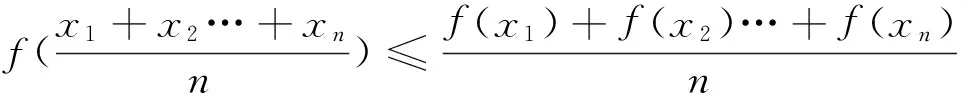
若f(x)在D内下凹上凸(即对于任意x∈D都有二阶导数f″(x)<0)且连续,则就把上面的“≤”替换成“≥”.
琴生不等式的加权形式:若f(x)在区间D内是上凹下凸的连续函数,则对任意的n(≥2)个实数x1、x2、…、xn∈D,及μ1、μ2、…、μn∈R+(其中μ1+μ2+…+μn=1),则恒有不等式f(μ1x1+μ2x2+…+μnxn) ≤μ1f(x1)+μ2f(x2)+…+μnf(xn)(其中“≤”当且仅当x1=x2=…=xn时取“=”);
若f(x)在D内是下凹上凸的连续函数,则就把上面的“≤”替换成“≥”.
下面例谈琴生不等式的简洁运用,并说明琴生不等式的几何意义,使读者能够乐于选用并且还善于运用琴生不等式.

(A)q=r
(C)p=r

图1
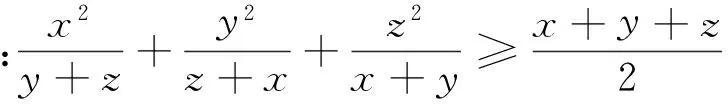
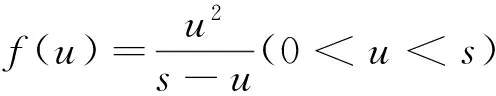
于是,函数f(x)区间(0,s)内是上凹下凸的函数,则运用琴生不等式得
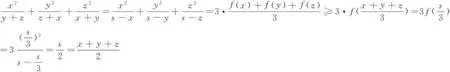
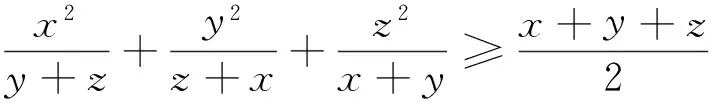
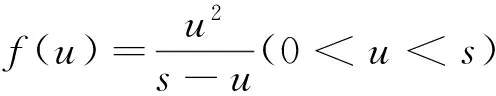
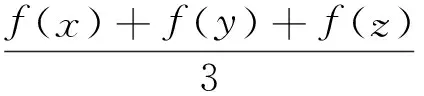
例3(2011年湖北高考压轴题)设bk(k=1,2,…,n)均为正数,若b1+b2+…+bn=1,证明:
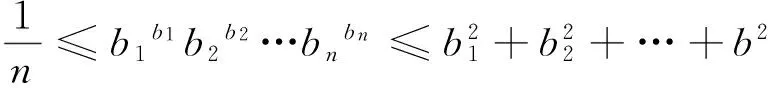
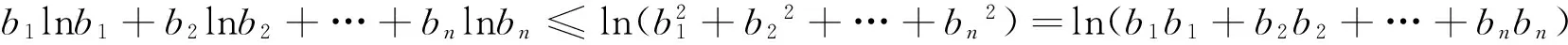



综合(1)、(2)得,原连接不等式正确.
补注:①此题是2005年全国高考压轴题的改编题;②这里两次构造的函数,都是用分析法所牵引出来的,这优于命题组提供的引理铺垫式的证法;③这里两次运用到琴生不等式,其第一次几何意义涉及凹凸函数图像的内接凸边形的加权重心,第二次几何意义类似于例2,请读者画出两个示意图.
为了既尽量节省篇幅又要展现琴生不等式的实用价值,下面列举用琴生不等式所能简洁解决的4道题目及提示,把解答过程留给读者完成.

提示:由琴生不等式和淘汰法,推测二阶导数f″(x)=0,构造f(x)=2x-1,填2047.
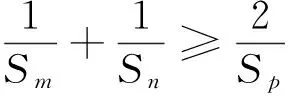

3.(2012年湖北高考末尾题改编题)给出一个命题:“设a1≥0,a2≥0,b1,b2为正有理数,若b1+b2=1,则a1b1a2b2≤a1b1+a2b2”.将上述命题推广到一般形式,并加以证明.
提示:推广命题为——“若a1、a2、…、an(其中n≥2)为非负实数,b1、b2、…、bn为正有理数,且b1+b2+…+bn=1,n≥2,则a1b1anbn…anbn≤a1b1+a2b2+…+anbn”.证法类似于例3.
4.(1)在△ABC中,求证:
cos2A+cos2B+cos2C+2cosAcosBcosC=1;
(2) (第20届伊朗奥数题)已知正数x、y、z满足x2+y2+z2+xyz=4,证明:x+y+z≤3.
[1]何先俊,罗伟.曲线凹凸性在高考选择题中的应用[J].中学数学月刊,2014(9):61-63.
[2]甘大旺.高考数学150专题[M].湖北教育出版社,2015:297-298.

