高中数学适性作业设计探究

浙江省台州市黄岩第二高级中学　(318000)

李　巧



高中数学适性作业设计探究

浙江省台州市黄岩第二高级中学(318000)

李巧

2004年，国内教育界开始提出“追求适合学生发展的教育”的理念.《国家中长期教育改革和发展规划纲要(2010―2020年)》明确指出，关心每个学生，促进每个学生主动的、生动活泼的发展，尊重教育规律和学生身心发展规律，为每个学生提供适合的教育.此后，“适性教育”的探索在全国多个学校展开.

“适性教育”是个性化教育，是人本教育，其思想核心主要体现为：根据学习者自身的差异性来实施与之相适应的最优质的教育或学习行为，这些行为贯穿教育实施的各个阶段.适性教育是根据学习者的差异有选择的进行教育，也是根据学习者的个性、人格、兴趣和能力的差异，进行灵活的选择教育.适性教育的提出首先是基于以学生为本这个出发点，适性教育最终是为了促进每个学生的健康成长.适性教育需要关注教学的全过程，在教学全过程中“尊重每一个、发现每一个、发展每一个”.

作业作为高中数学教学全过程中巩固环节的重要一环，也要讲究适性.目前的数学作业在设计上存在着难度过大，作业量过多等不适性现象，在深化课程改革的大背景下，文理科试卷又合二为一，对偏重文科的学生其要求在提高，在平时设计时如何做到“尊重每一个、发现每一个、发展每一个”，为每个学生提供适合的数学作业成为一个非常重要的课题.

基于适性教育的理念，适性教育下的高中数学适性作业设计应坚持如下原则.

1、计划性原则

作业是学生学习知识，开发智力，培养能力的系统学习过程.学生学习是一个循序渐进的过程，作为学习重要环节的作业，是与之同步的循序渐进的过程.如何执行作业行为，以达到形成技能之目的；什么阶段训练什么内容，采用什么方法，形成哪些技能，达到适性的目的等，都必须周密计划，才能保证作业有的放矢，有条不紊进行，保证作业质量，完成作业任务，达到适性作业的设计目标.

为提高作业安排的计划性，教师需根据阶段教学应达成的形成性教学目标，系统设计每天的作业，用可操作性的行为动词来表述作业的具体要求，并可以表格的形式提前一段时间告知学生.如此不仅教师自身能通盘安排教学资源，科学设计作业之间的衔接性，而且也能使学生清楚地把握阶段教学的轨迹，以便根据实际调整自己的学习行为.

时间作业类型形成性教学目标作业量新授阶段普适作业提升作业复习阶段章节复习普适作业提升作业专题复习普适作业提升作业

学考阶段作业的设计应在学业水平考试标准的指导下结合本校学生的实际有计划的按照标准来设计作业，建立作业题库. 在设计上应突出普适作业的设计，面向全体，根据基本要求，基础题的比例应在70%左右.高考复习阶段，应根据高中数学课程标准与普通高中学科教学指导意见，根据发展要求与学生实际来有计划设计作业，建立作业题库，拓展题与提高题的比例应加以提高.

2、层次性原则

学生的个体差异表现为认知方式与思维策略的不同，以及认知水平和学习能力的差异，教师要尊重学生的个体差异，满足多样化的学习需要.作业设计要考虑不同学习层次的学生不同的接受能力，提供多样性的作业选择，保证每一位学生得到主动发展.要难易适合，符合学生的身心特点和认知规律.

2.1普适作业——基础题

基础题要求人人去做，人人会做，是普适作业.重基础、重过程、重能力是近年来高考试题的特点.基础题在高考试题中占有很大的比重，因此重视基础题、提高基础题的解题正确率是取得好成绩的保证.基础题更加简洁地展示数学原理、方法与规律,是训练学生观察力和对问题的敏感度的重要素材,能起到“以简驭繁”的作用. 基础题有利于学生更好地掌握基础知识.对基础知识中存在的疑难问题，易混淆的概念等做好标记，对知识的重点、难点、疑点做到心中有数.要控制基础与提高的关系.如果过度做高难度题目，只会适得其反.正如笛卡儿所说:“从最简单、最易懂的对象开始,依照先后次序,一步步达到更为复杂的对象”,这也是学生必须明白的学习之道.

基础题作业要符合素质教育要求，布置学生完成的教师必须先做，以把握作业的难度与完成时间.每课时一页，半小时完成，全批全改.基础题作业库要做到及时更新.

如“圆锥曲线的综合问题”基础题：

3．过抛物线y2=4x的焦点作直线交抛物线于点A(x1，y1)，B(x2，y2)，若|AB|=7，则AB的中点M到抛物线准线的距离为()．

2.2提升作业——拓展题

教师应拓展学生的思维空间，不能让学生只停留对课本的理解和掌握上，要努力扩大学生的视野，设计要达到对知识的巩固和提高.要有利于培养学生的综合应用能力.教师应着力于提高学生解决问题的能力这一目标，拓展题的设计要突出综合性、应用性、灵活性、思想性、开放性.培养学生运用知识的能力，从而提高学生的数学综合素养.

拓展题可让学有余力的学生吃得饱，但如果设计得不恰当，不适度，学生跳一跳也摘不到果子，这样的设计适得其反，弄巧成拙.教师应根据学生的学习愿望及其发展的可能性，因材设题.拓展延伸题的安排，必须在教师认真钻研教材，明确教学目标的基础上来设计.

如“圆锥曲线的综合问题”拓展题：

1.圆锥曲线中的范围、最值问题

(1)若点P关于x轴的对称点为M，求证：直线MQ经过抛物线C的焦点F；

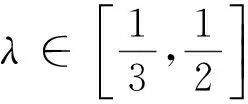
2.圆锥曲线中的定点、定值问题

(1)求椭圆C的方程；

(2)E、F是椭圆C上的两个动点，如果直线AE的斜率与AF的斜率互为相反数，证明直线EF的斜率为定值，并求出这个定值．

3.圆锥曲线中的探索性问题

已知中心在坐标原点O的椭圆C经过点A(2,3)，且点F(2,0)为其右焦点．

(1)求椭圆C的方程；

(2)是否存在平行于OA的直线l，使得直线l与椭圆C有公共点，且直线OA与l的距离等于4？若存在，求出直线l的方程；若不存在，说明理由．

数学源于生活，应用于生活.教师要善于联系生活实际进行基础题与拓展题的设计，充分展现数学的应用价值，让每一位学生在生活情境中体会“处处有数学”.教师在设计分层作业时，要善于主动地从数学的角度，运用数学的思维方法，多选择学生感兴趣的社会生活主题.

图1

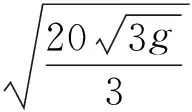
此题针对我国大量造舰，保卫海洋国土，引入相关习题，可有效激发学生的作业兴趣.

3、典型性原则

设计所学内容中的一些典型题目，从中去落实题中问题的基本方法、基本策略、基本思想．使学生对知识有一个再认知的过程，并且对一些常用的数学思想方法、基本策略有更多的实践体验.

3.1普适作业——样板题

样板题是指经过精选或精心设计的有代表性的例题. 要求教师对主干知识重点加以研究，进行纵向和横向的联想.“伤其十指，不如断其一指”，在每一章每一节的学习中，必须积累一些典型题目并经常对其进行研究和加以改编，形成样板题目.目的是通过课堂解题指导学生学会审题，形成解题思路，总结规律和技巧，在掌握重要知识的同时重在培养方法.样板题要求不同层次的学生都掌握好，是普适作业.

样板题在挑选与设计时要注意激发人人参与的机会，激励人人参与的能力，体会人人参与的成功，内化人人参与的意识；要强化学法指导.通过样板题变“授人以鱼”为“授人以渔”，同时注意学法指导的基础性与发展性.在引导学生形成基础性学习方法的同时，重视学生的发展性学习，让学生能够用已学方法，去解决新情况、新问题.

如“圆锥曲线的综合问题”样板题.

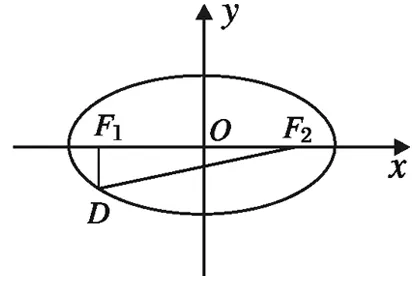
图2

(1)求该椭圆的标准方程；

(2)是否存在圆心在y轴上的圆，使圆在x轴的上方与椭圆有两个交点，且圆在这两个交点处的两条切线相互垂直并分别过不同的焦点？若存在，求出圆的方程；若不存在，请说明理由．

规律方法总结：求解椭圆的标准方程时，要根据已知条件利用椭圆的几何性质或椭圆的定义求解椭圆的基本量，得到椭圆的标准方程．对于直线与圆、直线与椭圆、圆与椭圆的位置关系，由于关系的错综复杂很难理清头绪，此时可以借助图形的特点，作出图形辅助求解，利用直线与圆锥曲线的位置关系解答，对于未知量可以利用先设后求或设而不求的方法来处理．

3.2提升作业——变式题

变式题是指变更概念中的非本质特征,变换问题中的形式、条件或结论,而概念或问题的本质不变的题目.教师改变原来题目中的某些条件或结论，使之成为一个新题.这种新题是由原来的比较典型的题目改编而来的，称之为变式题.改编原题是一项十分严谨、细致而周密的工作，要反复推敲，字斟句酌.每年的高考试题中都有一些似曾相识题，这种似曾相识题实际上就是变式题.

为了训练和培养学生运用知识解决问题的能力，进行变式训练是十分必要和有效的，变式作业训练让学生有机会从多角度、多侧面、多层次、多结论等方面去认识知识，学生的创造性思维得到了发展，思维活动的质量得到提高.

如“圆锥曲线的综合问题”变式题：

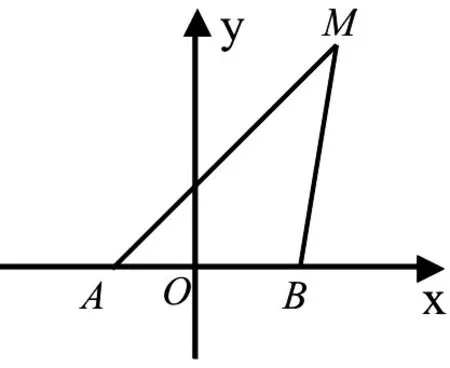
图3

1．如图3，动点M与两定点A(-1,0)、B(1,0)构成△MAB，且直线MA、MB的斜率之积为4.设动点M的轨迹为C.

(1)求轨迹C的方程；

(1)求椭圆C的标准方程；

(2)若直线l：y=kx+m与椭圆C相交于A，B两点(A，B不是左，右顶点)，且以AB为直径的圆过椭圆C的右顶点，求证：直线l过定点，并求出该定点的坐标．

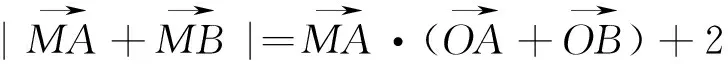
(1)求曲线C的方程；

(2)动点Q(x0，y0)(-2

变式题在新颖性要求上较高，以充分提高学生的应变能力.新形式新情境能更真实地考查出学生的实际能力.为提高试题的效度，高考命题注重材料新、视角新、观念新、表述新、形式新，避免重复特别是简单重复，以测评考生的真实水准.作业设计时要编选让学生耳目一新的真题、模拟题，提升学生的兴趣，激发做题的欲望，培养应变的能力.

样板题与变式题，突出的是万变不离其宗，以更好地掌握核心主干知识，促使学生思维活动得到质的提高，有效形成和掌握数学思想方法. 数学思想方法从接受的难易程度可分为三个层次： 一是基本具体的数学方法，如配方法、换元法、待定系数法、归纳法与演绎法等；二是科学的逻辑方法，如观察、归纳、类比、抽象概括等方法，以及分析法、综合法与反证法等逻辑方法；三是数学思想，如数形结合的思想、函数与方程的思想、分类讨论的思想及化归与转化的思想.高中数学教学的根本目的在于通过数学知识和观念的培养，通过数学思想的培育，让学生形成一种“数学头脑”，使他们在观察问题和提出问题、解决问题的每一个过程中，带有“数学色彩”，这样的数学一定会有真正的实效和长效，真正提高每位学生的数学素养.

[1]钱伟. 适性教育 渐行渐近的教育理想[J].基础教育参考，2012(10)：24-25.