简化函数结构 破解复杂问题

内蒙古师范大学附属中学(010020)

王洪军



简化函数结构破解复杂问题

内蒙古师范大学附属中学(010020)

王洪军

函数内容贯穿整个高中数学，尤其借助导数工具来研究函数问题，使得设计题目更加灵活，难度也更大，每当学生遇到此类问题，往往盲目进行尝试，徒劳无功. 其实好多函数问题在处理时都需要仔细观察其结构的，不妨将函数中复杂的部分记为f(x)×g(x)，按处理问题的难易程度依次分为如下几种：①f(x)为指数型且g(x)为对数型；②f(x)为指数型(或对数型)且g(x)为分式型；③f(x)为指数型(或对数型)且g(x)为多项式型；④f(x)和g(x)均为分式型；⑤f(x)和g(x)均为多项式型. 对于复杂的函数问题，好多情况都是因为函数的结构复杂，有时我们只需将结构简化，问题便会迎刃而解.下面我们通过具体实例来体会其中意义.

例1(2014年新课标全国Ⅰ卷理科21题)

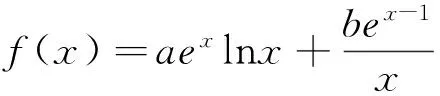
(1)求a，b； (2)证明：f(x)>1.

评注：通过将待证式转化为上述(*)式，使得复杂的函数结构变得相对简单，再通过常用的一个不等式(当x>0时，有ex>x+1)进一步简化函数的结构，问题便迎刃而解了.

下面再给出两种利用常用不等式简化函数结构的证法.

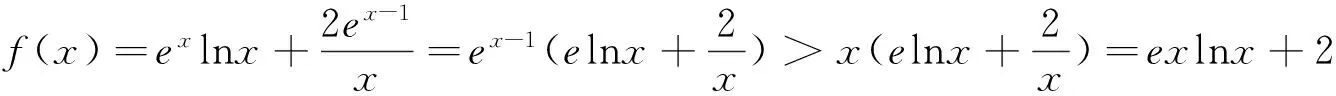
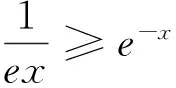
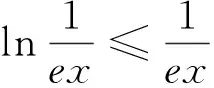
例2(2011年新课标全国卷文科21题)

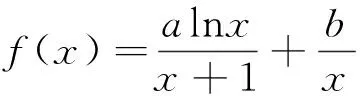
(1)求a，b的值；

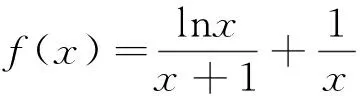
通过前面论述，我们能看到简化函数结构对解题的帮助，数学解题本身是一门实践性技术，经历实践、认识、再实践、再认识的过程，高考卷中的典型问题是值得反复推敲的.本文从这些函数实例中通过简化函数结构寻求处理问题的一般方法. 对于复杂的问题，智者见智，希望能对读者有所启发.