“特殊化”策略在课标卷数学试题中的应用赏析

福建省莆田第六中学　(351111)

陈瑞清

福建省漳州一中　　　(363000)

林新建



“特殊化”策略在课标卷数学试题中的应用赏析

福建省莆田第六中学(351111)

陈瑞清

福建省漳州一中(363000)

林新建

“特殊化”是重要的数学解题策略之一，是“特殊与一般思想”在数学解题中的应用.

它是通过选取特殊元素，依据问题在一般情况下真则在特殊情况下亦真，反之，在特殊情况下不真则在一般情况下亦不真的原理——肯定某一结论或否定其余结论的过程.

特殊化策略在解决某些数学选择题与填空题上有重要的作用，可以帮助我们快捷地得到问题的答案.

以下就它在课标卷试题中的应用举例赏析，以飨读者.

例1(2014年高考课标全国卷Ⅰ第8题)

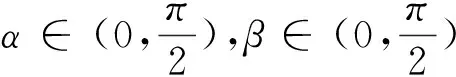
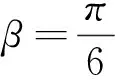
例2(2010年高考新课标卷Ⅰ理科11题)

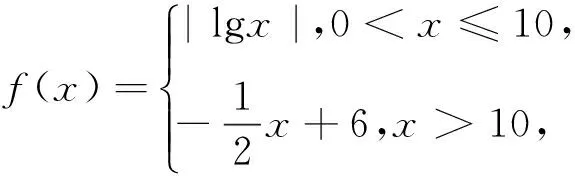
A．(1,10)B．(5,6)

C．(10,12)D．(20,24)

例3(2009年高考全国卷Ⅰ理科11题)

函数f(x)的定义域为R，若f(x+1)与f(x-1)都是奇函数，则().

A.f(x)是偶函数B.f(x)是奇函数

C.f(x)=f(x+2)D.f(x+3)是奇函数

解析：本题涉及抽象函数，直接求解难度较大，需由f(x+1)是奇函数得到f(-x+1)=-f(x+1)，由f(x-1)是奇函数得到f(-x-1)=-f(x-1)，进而得到f(-x+1)=f(-x-3)，故f(x)是以4为周期的周期函数，从而由f(x-1)是奇函数知f(x+3)也是奇函数，所以正确答案为D.

其实，本题是一个一般性问题，若运用特殊化策略予以求解轻松异常.

例4(2012年高考全国新课标卷理科16题)

数列{an}满足an+1+(-1)nan=2n-1，则{an}的前60项和为_________.

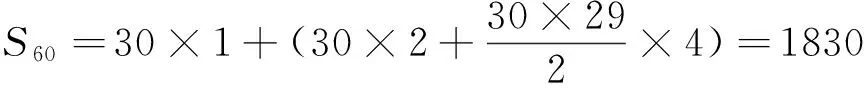
例5(2013年高考新课标卷Ⅰ理科11题)

A．(-∞,0]B．(-∞,1]

C．[-2,1] D．[-2,0]

解析：本题按常规方法求解较为繁琐，若能结合选择题的特征运用特殊化策略予以求解，简直不费吹灰之力.取x=-1，得a≥-3，可排除选项A、B；取x=1，则a≤ln2<1，可排除选项C，故正确选项为D.

例6(2015年高考新课标卷Ⅰ理科12题)

设函数f(x)=ex(2x-1)-ax+a，其中a<1，若存在唯一的整数x0使得f(x0)<0，则a的取值范围是().

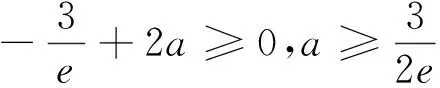
例7(2013年高考新课标卷Ⅰ理科16题)

若函数f(x)=(1-x2)(x2+ax+b)的图像关于直线x=-2对称，则f(x)的最大值是_________.

解析：本题也是个难题，求解的难点在于如何求出a、b的值.其实，若运用特殊化策略取特值可轻松求出a、b的值.由f(-4)=f(0)，f(-3)=f(-1)得-15(16-4a+b)=b，-8(9-3a+b)=0，联立解得a=8，b=15，从而f(x)=(1-x2)(x2+8x+15)=-(x+1)(x-1)(x+3)(x+5)=-(x2+4x+3)(x2+4x-5).令x2+4x=t，则t≥-4，y=-(t+3)(t-5)=-(t2-2t-15)=-(t-1)2+16≤16，当且仅当t=1时“=”成立，所以f(x)的最大值为16.