好题如好酒，越品味越浓——以2014年浙江理科数学第21题为例

浙江省德清县第三中学　(313201)

尹　文　施刚良



好题如好酒，越品味越浓
——以2014年浙江理科数学第21题为例

浙江省德清县第三中学(313201)

尹文施刚良

2014年浙江理科数学第21题是一道非常不错的试题，给人耳目一新的感觉.好的试题就像一坛陈年佳酿，打开盖子酒香马上扑面而来，光靠闻一下就知道肯定是好酒.如果再加以细细地品尝的话，那就“别有一番风味”了.

一、试题及解答呈现

2014年浙江理科数学第21题：

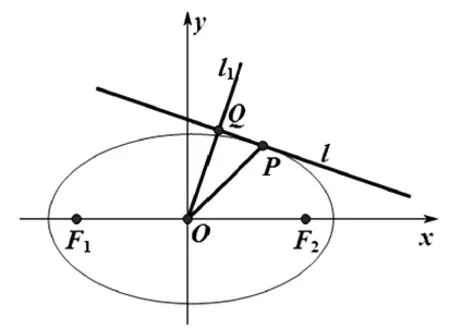
图1

(1)已知直线l的斜率为k，用a,b,k表示点P的坐标；

(2)若过原点O的直线l1与l垂直，证明：点P到直线l1的距离的最大值为a-b.

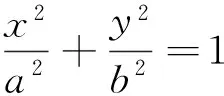
评注：标准答案通过设直线l的斜率k，然后联立直线与椭圆方程，令Δ=0得到点P的坐标；再利用点到直线的距离公式结合基本不等式求得点P到直线l1距离的最大值为a-b.这种思路比较自然、流畅，但计算量相对偏大，而且处理的都是字母之间的运算，可以说“击中”了学生的“软肋”，学生往往半途而废.分析上面的解题过程，试题设定了直线l的斜率k，通过层层设问，给学生作铺垫，让学生按照试题的要求去做，当然可以降低学生的解题难度，体现命题者对考生的“人文关怀”，但不利于学生创造性思维的发挥.瑕不掩疵，这道试题还是非常好的，让人觉得耳目一新，拍手称好!

二、试题的另解

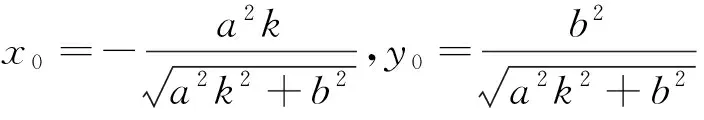
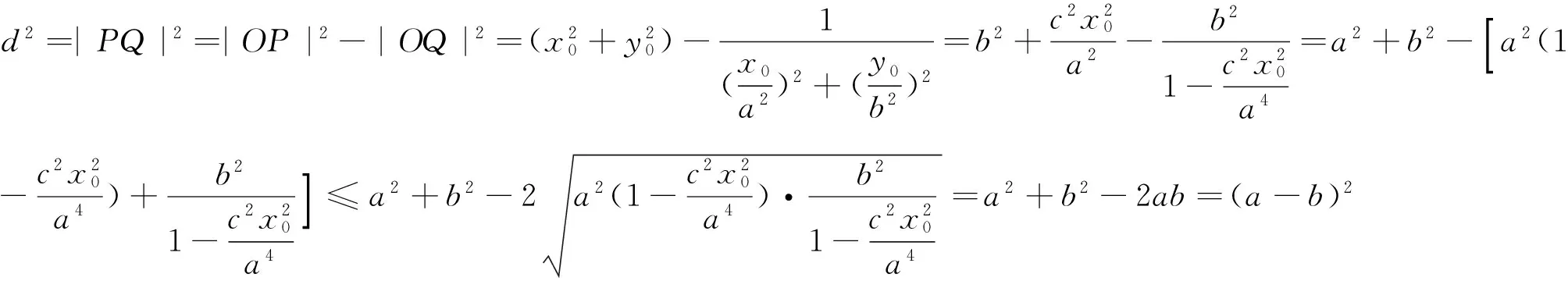
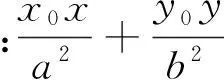
三、类比探究

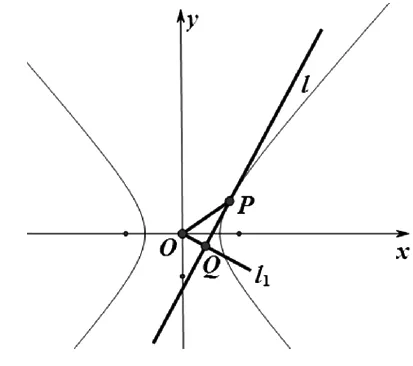
图2

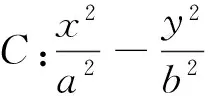
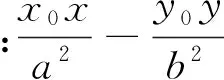
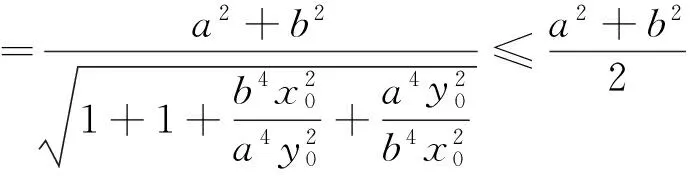
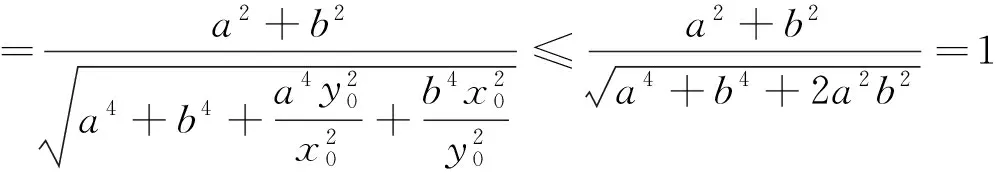
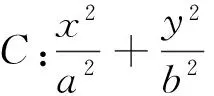
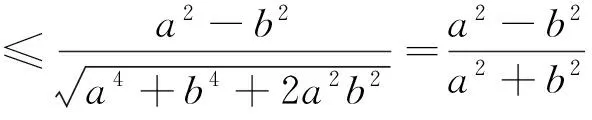
下面将上述探究的结论叙述如下：

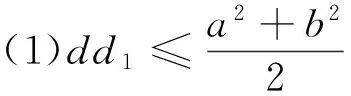
上面笔者通过深入挖掘和探究，得到了有心圆锥曲线的两个性质，于是很自然地就会提出问题：

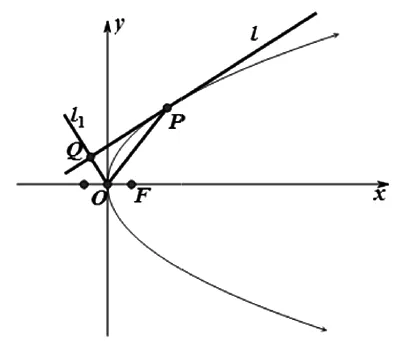
图3

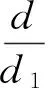
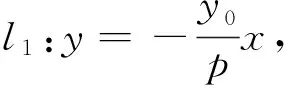
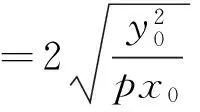
四、结束语

2014年浙江省的理科圆锥曲线试题较往年有所不同，以往都是第1问求圆锥曲线的标准方程，第2问求相关的最值或取值范围问题.而2014年的这道试题的结论具有一般性，让人耳目一新，能有效地考察学生的运算能力和数学思维能力，是一道很好的试题.同时，这道试题为我们一线教师进一步探究提供了绝佳的机会，上面笔者的探究历程就是很好的印证，当然也说明这道试题所蕴含的价值.好的试题犹如一坛美酒，随着时间的推移会越发地散发出迷人的酒香，正所谓“酒香不怕巷子深，题好不怕没人探”，我们一线教师期待命题者能多出这样的好题.

[1]邢友宝.莫为浮云遮望眼——例谈“简中求道”思想指导下的问题解决[J].数学通讯，2014(4)(下半月).