例谈平面向量数量积问题的求解策略

江西省信丰中学　(341600)

杜菊森



例谈平面向量数量积问题的求解策略

江西省信丰中学(341600)

杜菊森

平面向量知识是高中数学重要内容，也是高考的重要考点，尤其是平面向量的数量积问题，经常出现在选择填空的压轴题中，近几年高考命题的频率比较高，考生在处理这类问题时，经常感到无助，不知从何处入手．作为教育一线的教师，笔者对近几年各个省份有关平面向量数量积问题的高考题和模考题进行了系统的整理，归纳出了求解平面向量数量积问题的几种策略，以供大家参考与学习．

策略一、直角坐标法

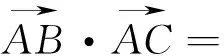
解：以点M为原点，MC所在直线为x轴的正方

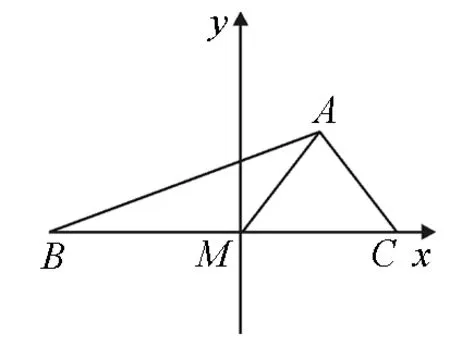
图1

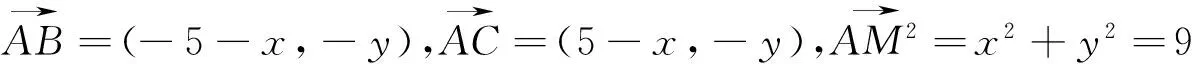
策略二、向量基底法

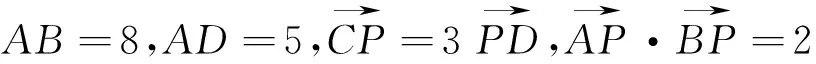
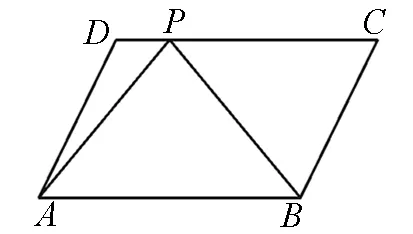
图2

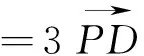
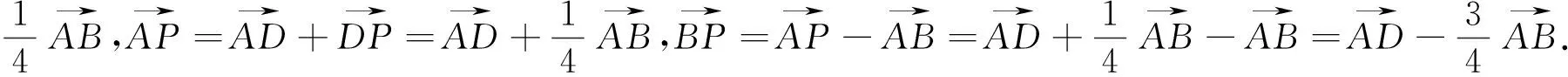
策略三、几何意义法(投影法)

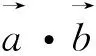
虽然深圳港驳船业务起步早，已具一定规模，但珠三角港口群的不断发展，使得深圳港早期高效、全面的服务优势逐渐下降.从深圳港水上“巴士”的班期稳定性、运价公开性、覆盖范围及对港口的贡献4个方面具体分析其存在的问题.

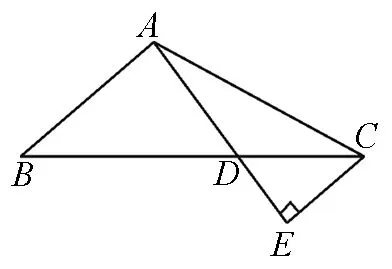
图3

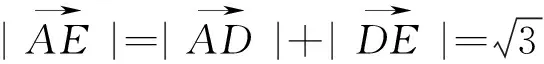
注:此题用坐标法解决也比较简单．

策略四、三角代换法

当平面向量语言所表述的几何元素为点时，且这样的点具有明显的圆的几何特征，那么我们就可以根据圆的参数方程，利用三角代换法解决平面向量数量积的问题．

图4

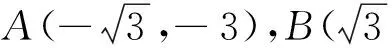
注:此题也可以用向量基底法来解，但要用到向量夹角余弦值的有界性．

策略五、构造函数法

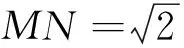
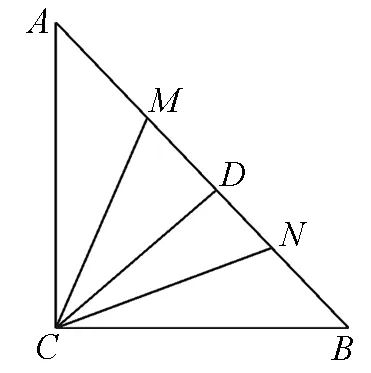
图5

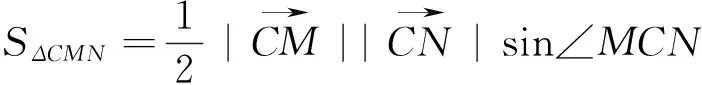
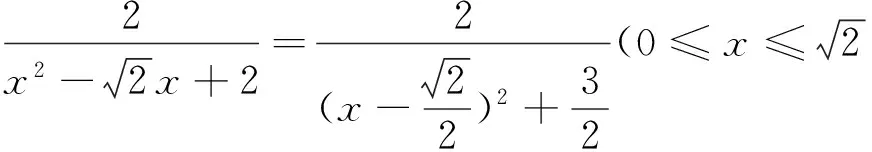
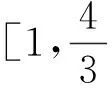
注:此题也可用坐标法来求解，但要设两个变量才能解决．

[1]彭晨辉．高中数学向量问题处理方法例析[J]．数理化解题研究(上旬)，2015(3)：32．

[2]肖浩春．一道平面向量数量积问题的多角度研究[J]．中学数学研究(上半月)，2015(6)：33-34．