一个欧拉不等式加强猜想的证明
广东省广雅中学 (510160)
杨志明
一个欧拉不等式加强猜想的证明
广东省广雅中学(510160)
杨志明
文[1]证明了文[2]提出的两个问题:
设 ΔABC 的三边为 a,b,c ,面积为 Δ ,外接圆和内切圆半径分别为 R,r ,则有
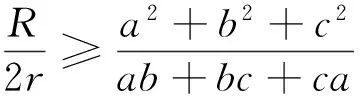
最后提出如下
猜想1设 ΔABC 的三边为 a,b,c ,面积为 Δ ,外接圆和内切圆半径分别为 R,r ,则有
经探讨发现,(3)式成立.
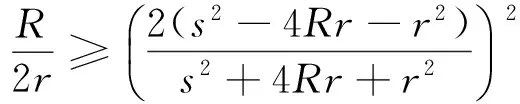
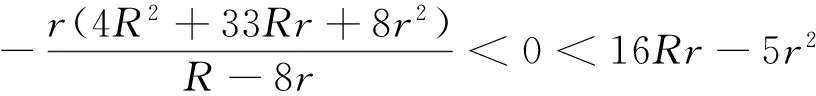
f(16Rr-5r2)=400R3r2-1312R2r3+1168Rr4-288r5=16r2(R-2r)(25R2-32Rr+9r2)=16r2(R-2r)[(9(R2+r2)+16R(R-2r)]≥0.当R=8r 时,R-8r=0,f(s2)=1056r2s2>0.当2r≤R<8r 时,R-8r<0,此时 f(s2) 是关于 s2的一元二次函数,且开口向下.
由Gerretsen不等式知, 16Rr-5r2≤s2≤4R2+4Rr+3r2.要证明 f(s2)≥0 ,只需证明 f(16Rr-5r2)≥0 且 f(4R2+4Rr+3r2)≥0 即可.f(16Rr-5r2)=400R3r2-1312R2r3+1168Rr4-288r5=16r2(R-2r)(25R2-32Rr+9r2)=16r2(R-2r)[(9(R2+r2)+16R(R-2r)]≥0.f(4R2+4Rr+3r2)=16R5-64R4r+96R3r2-64R2r3+16Rr4-32r5=16(R-2r)(R4-2R3r+2R2r2+r4)=16(R-2r)[R2(R-r)2+r2(R2+r2)]≥0.
综上可知,f(s2)≥0.
由(1)和(3)式不难提出如下猜想:
猜想2设ΔABC的三边为a,b,c,面积为 Δ ,外接圆和内切圆半径分别为 R,r ,则有
猜想3设ΔABC的三边为 a,b,c,面积为 Δ ,外接圆和内切圆半径分别为 R,r ,则有
猜想4设ΔABC的三边为 a,b,c,面积为 Δ ,外接圆和内切圆半径分别为 R,r ,则有

[1]马占山,何慧敏.一个与欧拉不等式相关的表达式问题的证明[J].中学数学研究(江西).2016,2.
[2]安振平.外森比克不等式的再探究[J].中学数学教学.2015,2.
[3]陈胜利.关于R,r与s的锐角三角形不等式.见:几何不等式在中国[M].江苏教育出版社,1996,6:72-78.

