一道调研试题的解题分析

浙江省宁波市第四中学　(315016)

张延斌



一道调研试题的解题分析

浙江省宁波市第四中学(315016)

张延斌

一、问题的提出

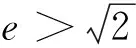
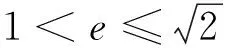
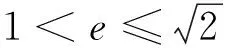
本题是浙江省新一轮课改高考前的调研试题，是其中选择题的最后一题.本文将全方位剖析这个问题.

二、选择题解法

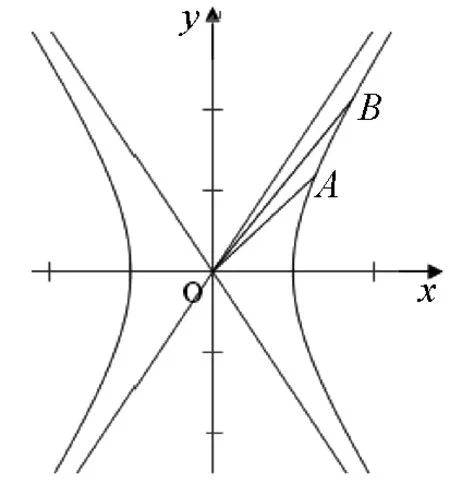
图1

作为选择题，无论是教师还是学生，首先关心的是答案的确定.

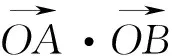
图2

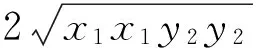
在对学生的测试调查中，发现大多数学生感觉无法直接下手，都是采用选择题的特殊化解法，但由于解决问题的思维力度不够，大多出错，另外一些学生属于“对而不会”.事实上，对于此题的分析，与一般的选择题解法一样，通过直觉思维直接进入解题环节.虽然运用了双曲线方程与最大(小)值的概念，这其中渗透了极限的思想，还需要有合乎逻辑的推理和解题的智慧性.

三、“错解”的启发

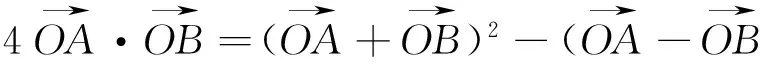
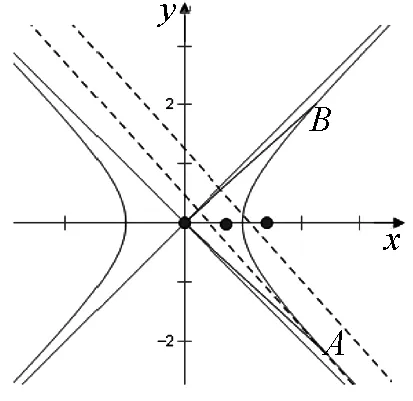
图3

显然这个解法是错误的，但给我们提供了一条解题思路，即先固定A(x1,y1)，令z=x1x+y1y，问题转化为直线z=x1x+y1y与双曲线C右支有公共点时z的最小值z(x,y)，然后再求z(x,y)的最小值.

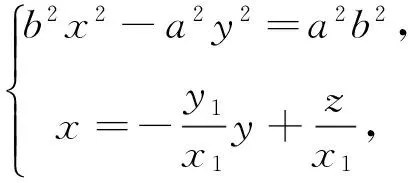
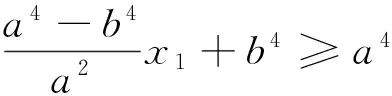
由于是个多变量的条件最值问题，从最小值的概念出发，可将y1,y2调控为y1y2≤0.据此，还可得如下的简捷解法：

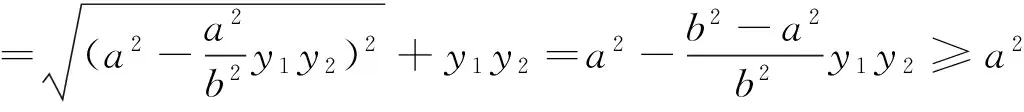
四、解法的完善

1 对参数方程的调控

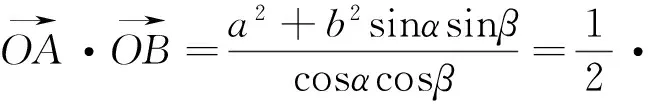
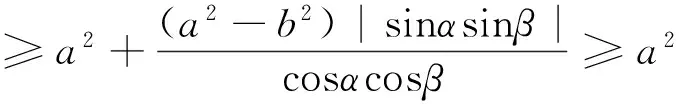
2　对联立方程的调控

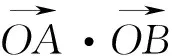
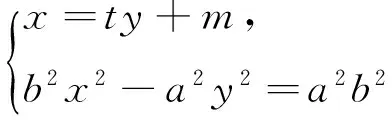
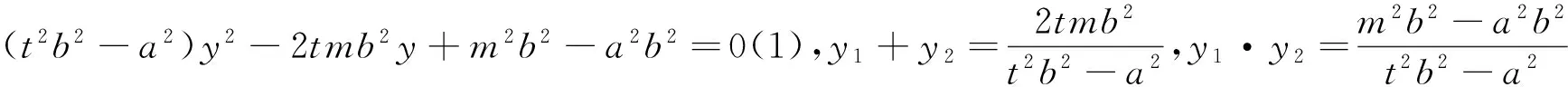
五、解题分析的反思

解题研究无禁区，课堂教学有范围，上述各个解法，书写长度与思维深度都会有所差异，哪些适于全体学生，哪些适于部分学生，作为课堂教学的试卷讲评分析，我们不能只让学生被这些解题技巧所吸引、震撼，而是要让各个层次的学生都得收益.为此，笔者以此题为素材开设了一堂探究性的解题教学课，取得较好的效果.其教学程序如下：

1．选项确定

作为一个选择题，确定它的答案是每个学生首先关心的.学生运用解答选择题的方法，通过特殊定位，一般核对，达到问题的“粗略”解答.

2．演绎推理

此时，学生兴奋点上来了，迫切希望问题严谨的解答.在这里选择二种学生上手后不能解决的方法进行分析.

3． 挖掘运用

由于本节课的核心问题是圆锥曲线与向量的数量积问题，如果把问题延伸到椭圆上，觉得意义不大.于是，在学生的学习激情不减的情况下，再燃一把火，推出三个习题加以操练.

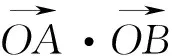
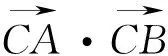
(A)CM⊥AB (B)CM⊥CB

(C)CM⊥CA(D)CM⊥l

(A)-15(B)-9(C)-7(D)-6

[1]罗增儒，数学解题引论[M].西安,陕西师范大学出版社.2007(7)：40-41.