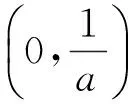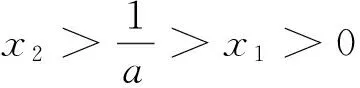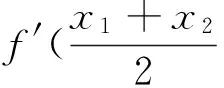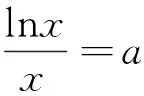对一道自主招生试题的探究

安徽省砀山中学　(235300)

胡云浩



对一道自主招生试题的探究

安徽省砀山中学(235300)

胡云浩

一、试题呈现

(2015年中国科学技术大学自主招生试题)

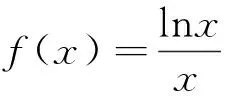
(Ⅰ)求函数f(x)的单调区间和最大值；

(Ⅱ)设02e.

本题主要考查函数的单调区间、极值、最值及函数两零点的和与极值点之间的大小关系等知识，题干简约，但内涵丰富、内蕴厚重，试题难度较大，很好地考查了学生分析问题、解决问题的能力.本文试图揭示此类问题的背景，探寻解题思路，明晰解题方法，优化解题过程，提高解题效率.

二、背景揭示

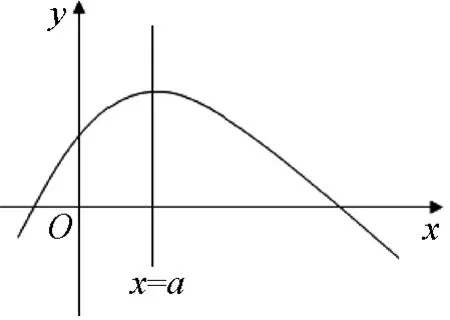
图1

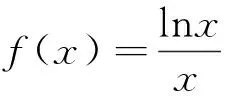
三、思路探寻

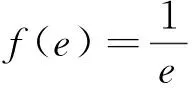
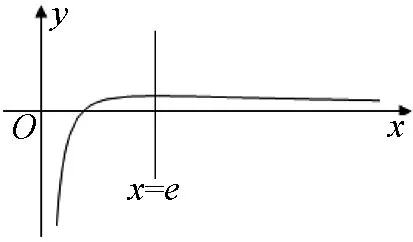
图2

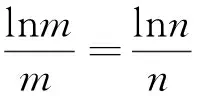
以上思路可概括为：已知函数f(x)是关于直线x=a的“类对称”函数，若f(x1)=f(x2)，要比较x1+x2与2a的大小关系，只要比较x1与2a-x2的大小即可.∵ f(x1)=f(x2),x1≠x2,a是函数f(x)的唯一极值点，∴x1,x2必在直线x=a的两侧，即x1与2a-x2必在f(x)的同一单调区间内，∴只要比较f(x1)与f(2a-x2)的大小即可，又f(x1)=f(x2)，故只需比较f(x2)与f(2a-x2)的大小即可.此思路简洁、自然，易于操作，具有程序化.

四、牛刀小试

(Ⅰ)求f(x)的单调区间；

(Ⅱ)证明：当f(x1)=f(x2)(x1≠x2) 时，x1+x2<0.

解析：(Ⅰ)f(x)在(-∞,0)上单调递增，在(0,+∞)上单调递减.

(Ⅱ)不妨设x1<0

∴当x>0时,F′(x)<0，∴F(x)在(0,+∞)上单调递减，∴F(x)

例2(2011年辽宁理科第21题)已知函数f(x)=lnx-ax2+(2-a)x.

(Ⅰ)讨论f(x)的单调性；

(Ⅲ)若函数y=f(x)的图像与x轴交于A,B两点，线段AB中点的横坐标为x0，证明f′(x0)<0.

例3(2015年安徽省江南十校联考第20题)已知函数f(x)=lnx-ax(a为常数).

(Ⅰ)若函数f(x)在x=1处的切线与x轴平行，求a的值；

(Ⅱ)若函数f(x)有两个不同零点m,n，证明m·n>e2.

解析：(Ⅰ)略；