基于SIMULINK的光伏电池模型及

景会成，徐来立，李静，玄兆燕，赵欣

(1.华北理工大学 电气工程学院，河北 唐山 063009；2.华北理工大学 机械工程学院，河北 唐山063009；3.唐山市拓又达科技有限公司，河北 唐山 063020)



基于SIMULINK的光伏电池模型及

模糊算法MPPT系统仿真

景会成1，徐来立1，李静1，玄兆燕2，赵欣3

(1.华北理工大学 电气工程学院，河北 唐山 063009；2.华北理工大学 机械工程学院，河北 唐山063009；3.唐山市拓又达科技有限公司，河北 唐山 063020)

光伏电池；仿真模型；simulink；MPPT；模糊算法；控制规则

以光伏电池等效电路图为基础，推导其等效数学模型，并进行简化改进，在此基础上建立光伏电池在simulink环境下的仿真模型。由其输入输出曲线可以看出，此模型能够很好地表现出光伏电池的输入输出特性。研究将模糊算法应用于该光伏电池仿真模型，并对控制规则加以改进，建立光伏电池MPPT系统仿真模型。仿真结果表明，该MPPT系统不仅能够较快地追踪到当前环境条件下的MPP,而且能够在环境突变后再次迅速追踪到系统的MPP，同时系统稳定后没有波动，为制作高效MPPT光伏控制器提供了依据。

0 引言

随着化石燃料的日益枯竭，人们越来越关注以太阳能为代表的可再生资源，各国政府也纷纷出台各种政策支持太阳能发电产业的发展。光伏电池是太阳能发电的重要部件，但是其在发电的过程中输出极易受负荷状态、日照强度、环境温度等外界因素的干扰，使输出功率变得很不稳定[1]，这导致其光能利用率大大降低。因此，掌握好光伏电池的输入输出特性，并对其施加合理的控制，对于更加高效地利用太阳能十分关键。研究以光伏电池的等效电路图为基础，推导出其数学模型，然后对其进行简化改进。在simulink中建立其仿真模型，得出其输入输出特性曲线，并以此为基础，应用模糊算法，建立基于模糊算法的光伏电池MPPT仿真系统。

1 光伏电池的仿真模型

光伏电池已经被各个行业广泛利用。其发电原理是当半导体的材料界面在阳光照射下会生成电压，从而将太阳能直接转变为电能。其输入输出特性能够用如图1所示的等效电路来描述[3]。

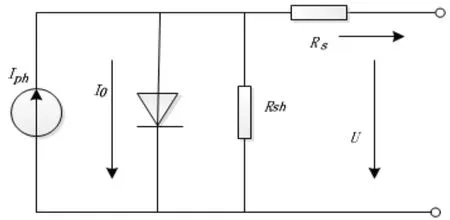
图1　光伏电池的等效电路

其中电流表达式为：

(1)

式中，Iph为光生电流；I0为光电池反向饱和电流；n为二极管的参数；k为玻尔兹曼常数；q为电子电量；Rs为光电池的串联电阻；Rsh为光电池的并联电阻。

实际上，在工程应用中确定(1)中的参数十分不便，很不实用。而且有时候生产厂家提供的参数也不能适合所有环境条件。文献[2]提出了一种比较实用的简化数学模型：

I=Isc(1-C1{exp[U/(C2Uoc)]-1})

(2)

C1=(1-Im/Isc)exp[-Um/(C2Uoc)]

(3)

C2=(Um/Uoc-1)/[ln(1-Im/Isc)]

(4)

在(2)、(3)、(4)式中，U、I分别为输出电压和电流，C1、C2为改进系数。Isc、Uoc、Im、Um等参数由光伏电池厂商提供。

但是，前面推导的光伏电池的等效数学模型还跟实际情况有一定的偏差。因此需要对U、I、C1、C24个参数进行改进。改进系数如下所示：

(5)

(6)

(7)

(8)

其中，参数a=0.002 5 ℃，b=0.5，c=0.002 88 ℃。S,T分别为光照强度和环境温度。在simulink环境中搭建光伏电池仿真模型，该模型输入量有光照强度S、环境温度T、输入电压U3个。2个输出量，分别为输出电流I和输出功率P。Simulink仿真模型如下图2所示：

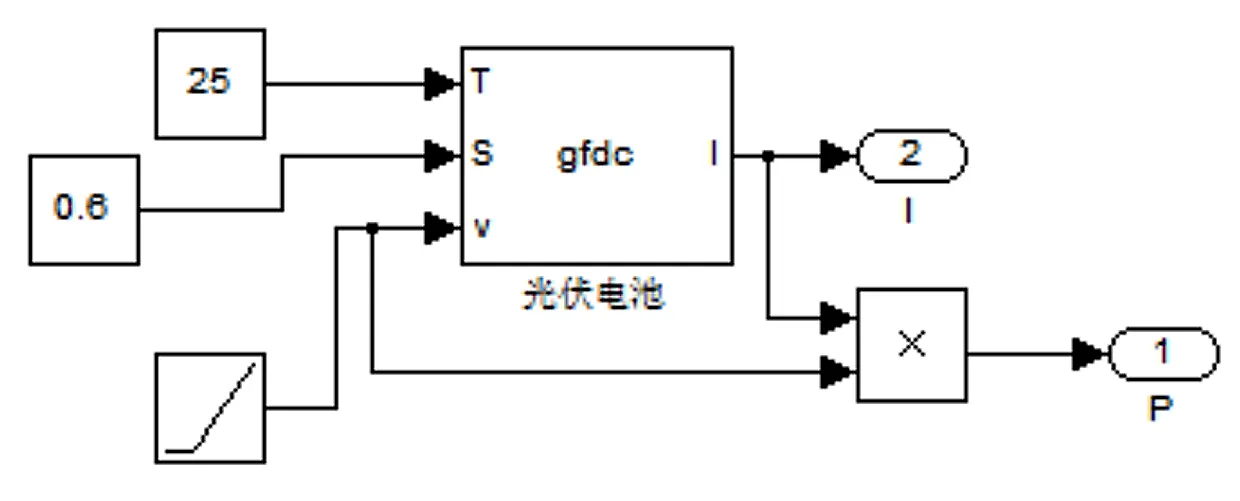
图2　光伏电池仿真模型

其中，“guangfu”模块为依据上述公式建立的光伏电池仿真模型的封装形式。图3中所示3条曲线，为该仿真模型在3种不同光照强度下的输出功率随输出电压变化曲线。由图3仿真曲线知，该模型能够很好地反映光伏电池输出功率-输出电压的变化情况。

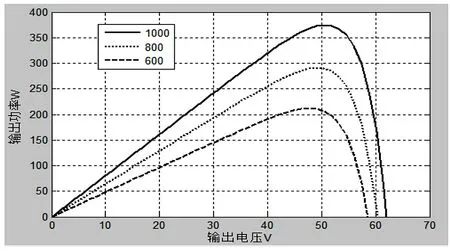
图3　光伏模型仿真曲线

2 光伏电池MPPT原理

由图3仿真曲线可以看出，在特定的光照强度和环境温度下，输出电压取不一样的值，输出功率相差很大。但是只有输出电压在某一个特定的值时，其输出功率达到该环境条件下的最大值，这时光伏电池工作在最大功率点(MPP)。但是，在实际应用中，外界的光照条件通常不能保持在相同的光照强度。由图3还可看出，当光照强度增大或减小时，其最大功率点也会变化。要提高系统的光能利用率，最有效的方法就是能够根据环境变化实时改变光伏电池的输出电压，使它总是等于当前环境下最大功率点处所对应的电压，这种实时调整过程就是MPPT。

为了能够实时改变其输出电压的大小，还需要加入DC/DC电压转换电路。通过改变电压转换电路mos开关管的输入占空比，不断改变光伏电池输出电压。这样当外界条件发生变化时，由控制算法对占空比进行调整，调节输出电压，这样就能追踪当前时刻的光伏电池的最大发电功率点，实现系统MPPT的控制。

3 最大功率点跟踪算法

对于实现MPPT的方法，目前在很多文献中都提出了各种各样的算法。其中比较常用的有扰动观察法、功率检测反馈法、增量电导法等等，各有优点。其中扰动观察法结构相对简单，并且需要测量的参数较少，但是在到达最大功率点之后，系统还会不停地添加扰动信号，这使得系统会在MPP左右震荡，系统不能稳定，造成能量的浪费。增量电导法，虽然可减小系统在最大功率点附近的左右震荡，使其能适应瞬息万变的环境条件，但是当系统使用的传感器无法达到非常精确时，其误差也是不可忽视的。

研究采用模糊算法跟踪系统的MPP，利用模糊规则智能地改变电压变换电路的输入占空比，不断改变电压值，从而找到系统的MPP。本方法结构简单，只需测量系统的输出功率，无论外界环境如何变化，都能使系统快速地跟踪到当前的MPP，且通过对模糊规则进行改进，使得系统在搜索到MPP后不存在震荡，从而效率更高。

4 模糊控制器的设计

4.1模糊控制器的设计流程

控制器设计流程如图4所示。在系统仿真过程中，若控制器的性能达不到要求，则需要重新确定隶属度函数，或者重新确定系统的输入输出量。

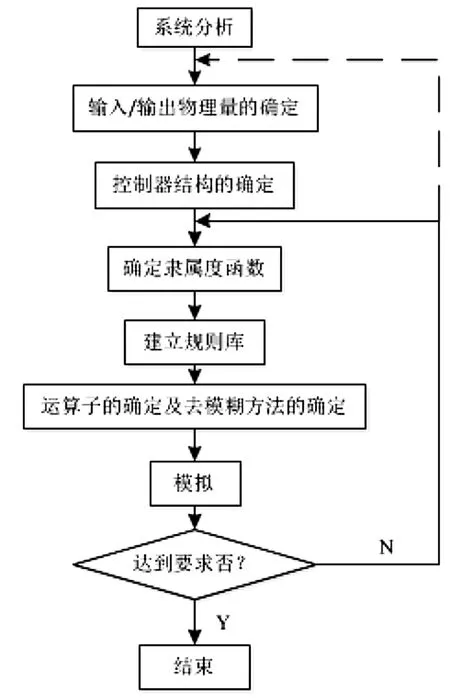
图4　模糊控制器设计流程

4.2MPPT的模糊算法

MPPT本质上是一个寻优过程[1]。通过测量光伏电池输出的功率变化，比较上一时刻控制器输出的占空比的调整值，判断当前状态与峰值功率点的位置关系，通过调整占空比输出调整值，使功率向增大的方向变化[4]，直到达到最大功率。但当环境变化时会使最大功率点产生漂移，这时，模糊控制器也可以检测到这种变化，并对输出的占空比调整值进行调整，使系统重新工作到最大功率点。

选取模糊控制器输入量为前后2次采样功率变化量和上一次采样占空比调整值，输出量为当前采样占空比需要的调整值。如上图5所示，控制器第n次采样的输入量为第n次采样功率值相对于第n-1次采样功率值得变化量e(n)和第n-1次采样的模糊控制器输出占空比需要调整值a(n-1)，分别乘以各自的量化因子后输入到控制器。输出量为控制器第n次采样占空比需要调整值A(n)乘以量化因子。图中，e(n)和a(n)分别表示实际值；E(n)和A(n)分别表示模糊论域中的值。D(n)和D(n-1)分别为第n次和n-1次采样后输入到变换器的PWM占空比的值,Ke，Ka分别为量化因子。

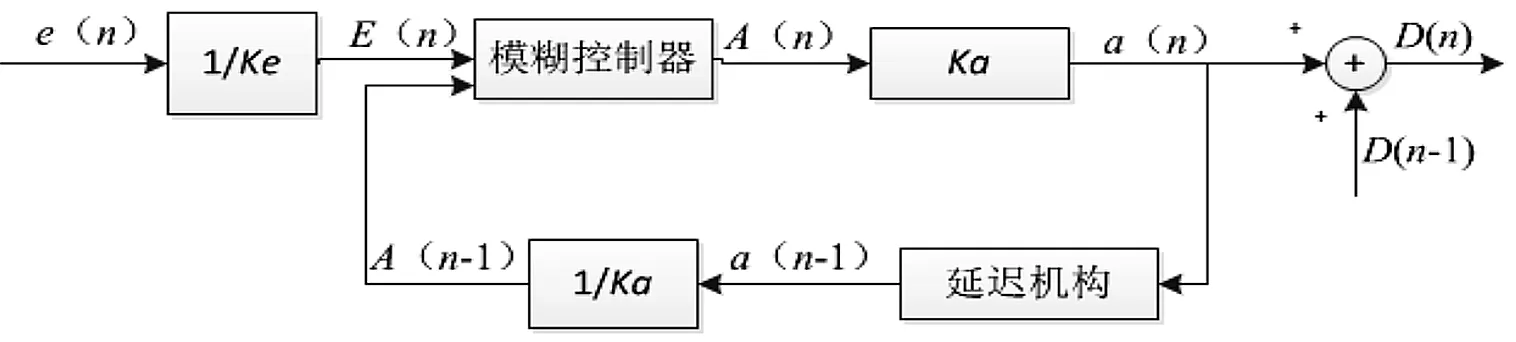
图5　模糊控制系统框图

控制器根据系统前后2次采样输出功率值的变化量和前一次采样占空比需要调整值的大小，决定当前采样占空比需要输出的调整值。若系统在发电过程中的输出功率增加，则控制器输出正的调整值，否则输出负的调整值；当光伏电池工作在离MPP较远处时，模糊控制器输出较大的调整值，以加快跟踪速度；当工作在MPP附近时，输出较小的调整值，从而减小功率损失。

根据上述原理，并在实际仿真进行中反复进行调整制定出控制规则表，如表1所示。

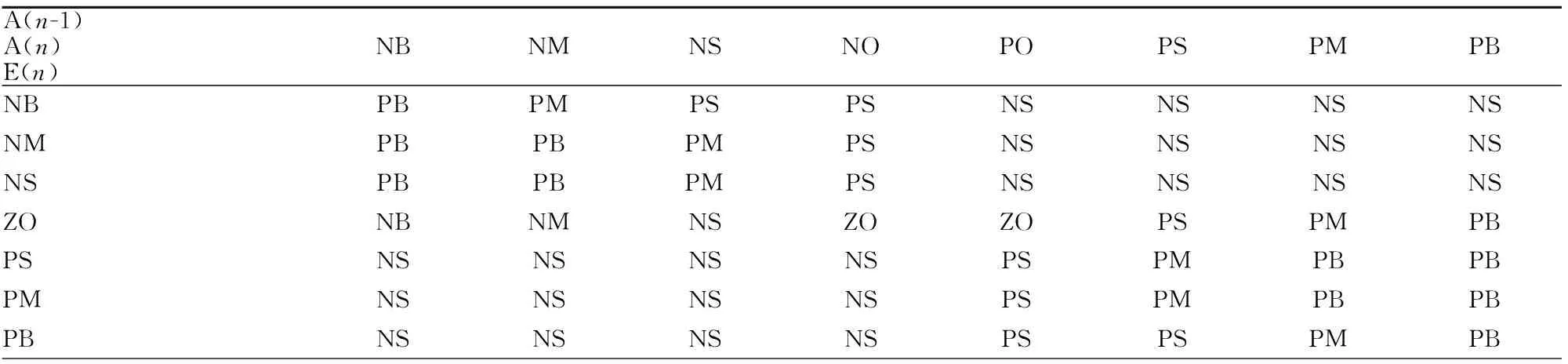
表1　模糊控制规则表

4.3MPPT模糊控制系统SIMULINK仿真

利用matlab软件中的模糊逻辑工具箱，建立基于模糊算法的MPPT系统的仿真模型[5]。

4.3.1确定输入/输出变量以及控制器结构的选取

将输入变量E和A的语言取值分别定义为8个和7个模糊子集，即

E={NB,NM,MS,NO,PO,PS,PM,PB}

A={NB,NM,NS,ZO,PS,PM,PB}

并将它们的论域规定为14个和12个等级，即

E={-6,-5,-4,-3,-2,-1,-0,+0,+1,+2,+3,+4,+5,+6}

A={-6,-5,-4,-3,-2,-1,0,+1,+2,+3,+4,+5,+6}

选择如图6所示的控制器结构。

4.3.2确定隶属度函数

输入输出变量都选择三角形隶属度函数，其中功率差值E和占空比需要调整值A的隶属度函数如图6所示。

(a)功率差值E的隶属度函数

(b)占空比需要调整值A的隶属度函数

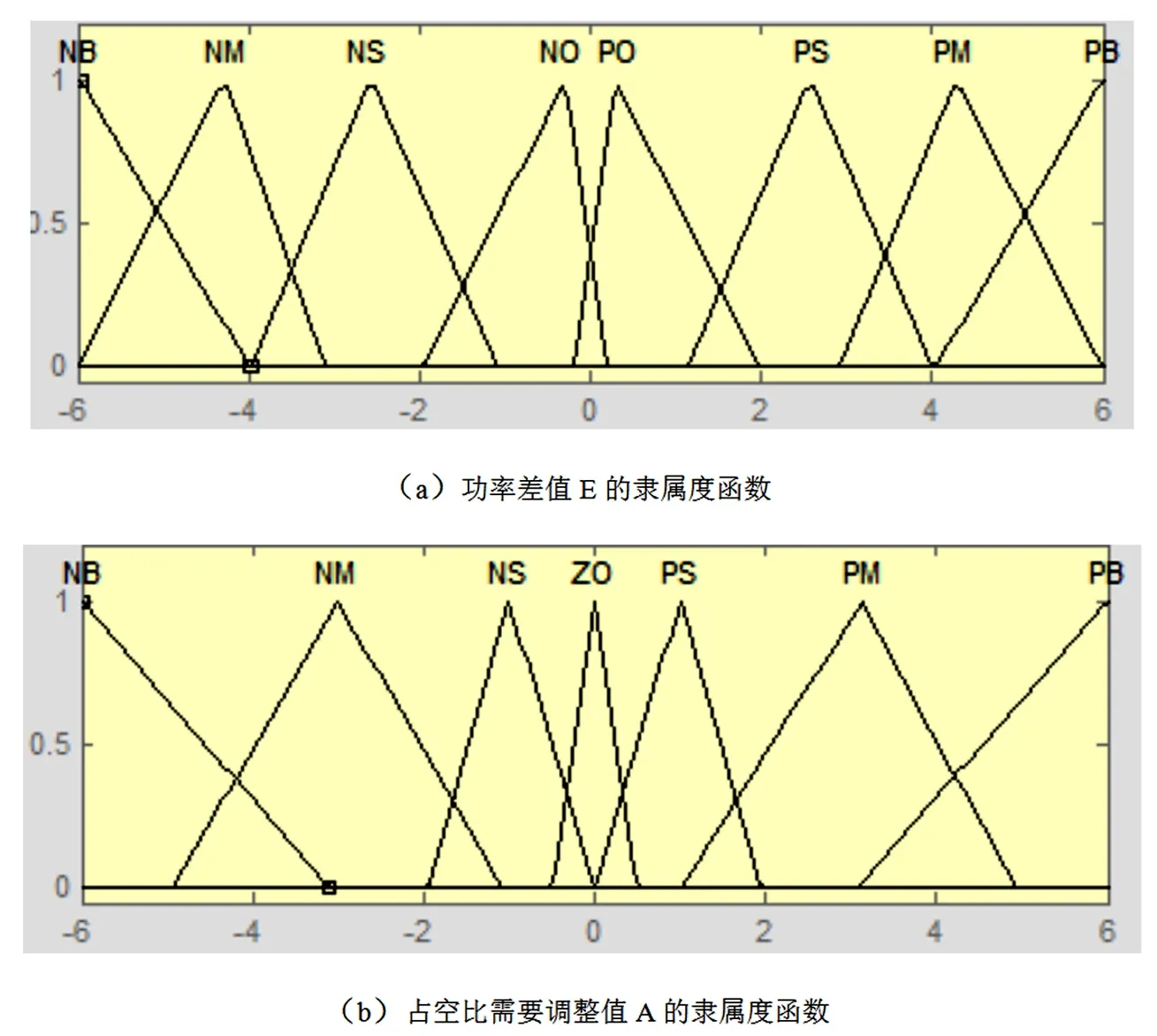
图6　隶属度函数

4.3.3 确定模糊规则

打开模糊规则编辑页面，将表1中的56条规则逐条添加进去。

4.3.4 解模糊

在matlab的属性编辑页面，将参数设置完毕。

5 仿真结果

搭建好的系统仿真模型如图7所示；其中系统经过反复的试验，量化因子Ka取0.003，Ke取10/3。

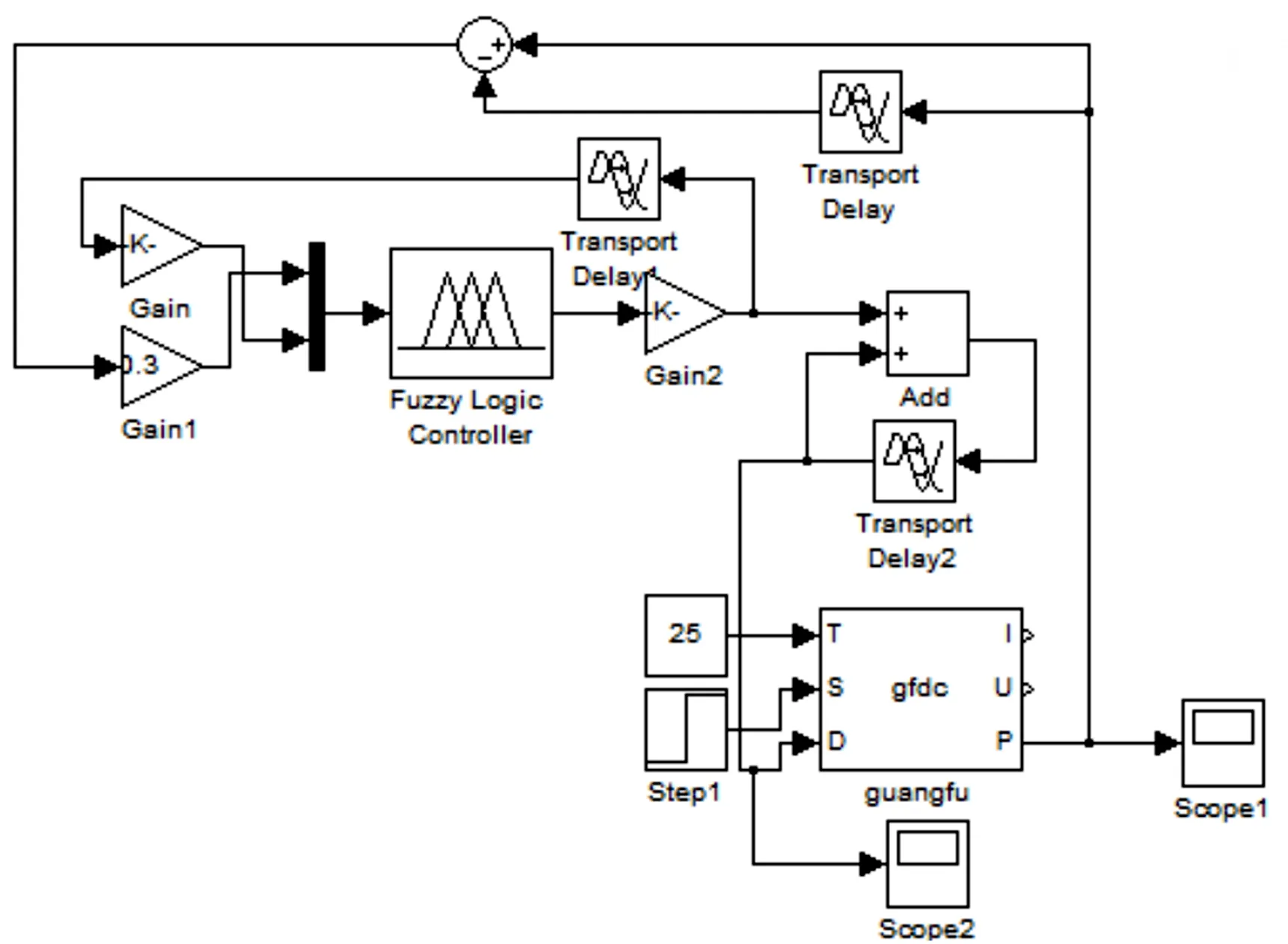
图7　SIMULINK环境下MPPT系统仿真模型

将环境温度设置为25 ℃，分别模拟日照强度从800 W/m2突然增大到1 000 W/m2和模拟日照强度从800 W/m2突然减小到600 W/m2的情况。将系统仿真最大步长设定为0.02 s，运行时间设定为6 s，延迟时间为0.025 s。分别得到系统输入占空比和输出功率在2种情况下的波形变化图如图8和图9所示。

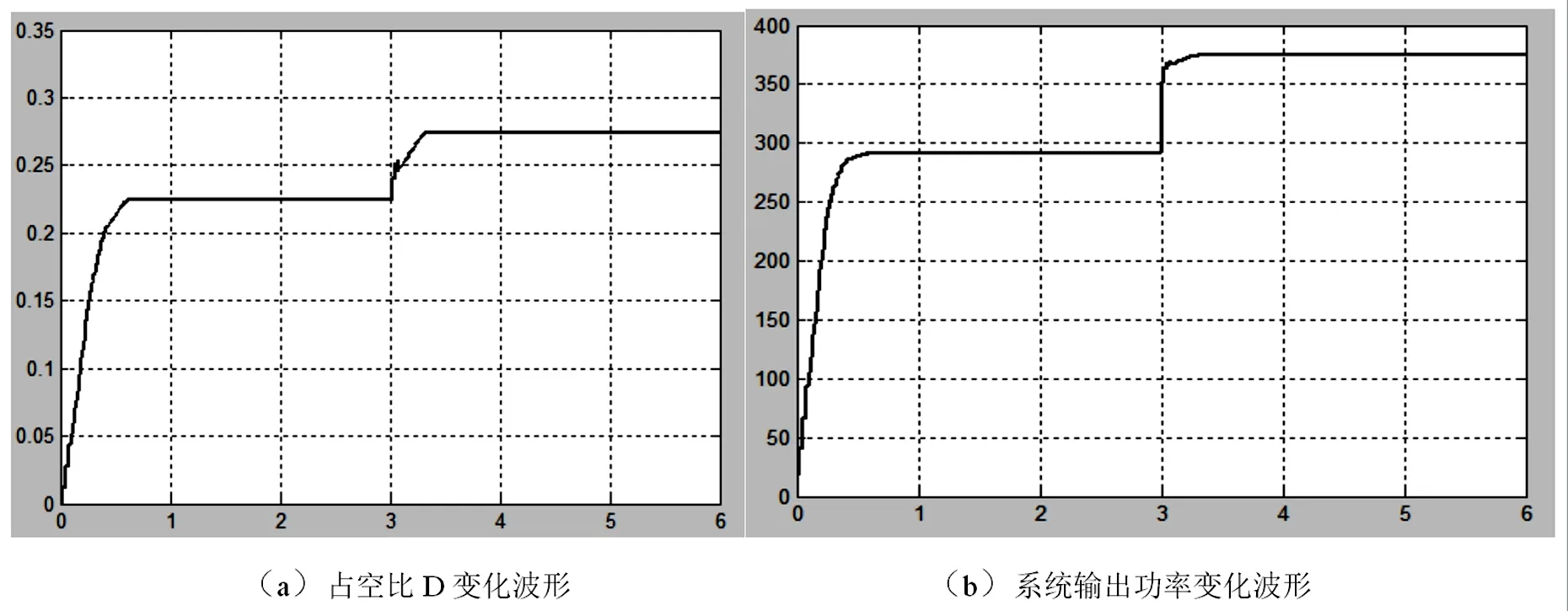
图8　系统光照从800 W/m2突然增大到1 000 W/m2系统仿真波形

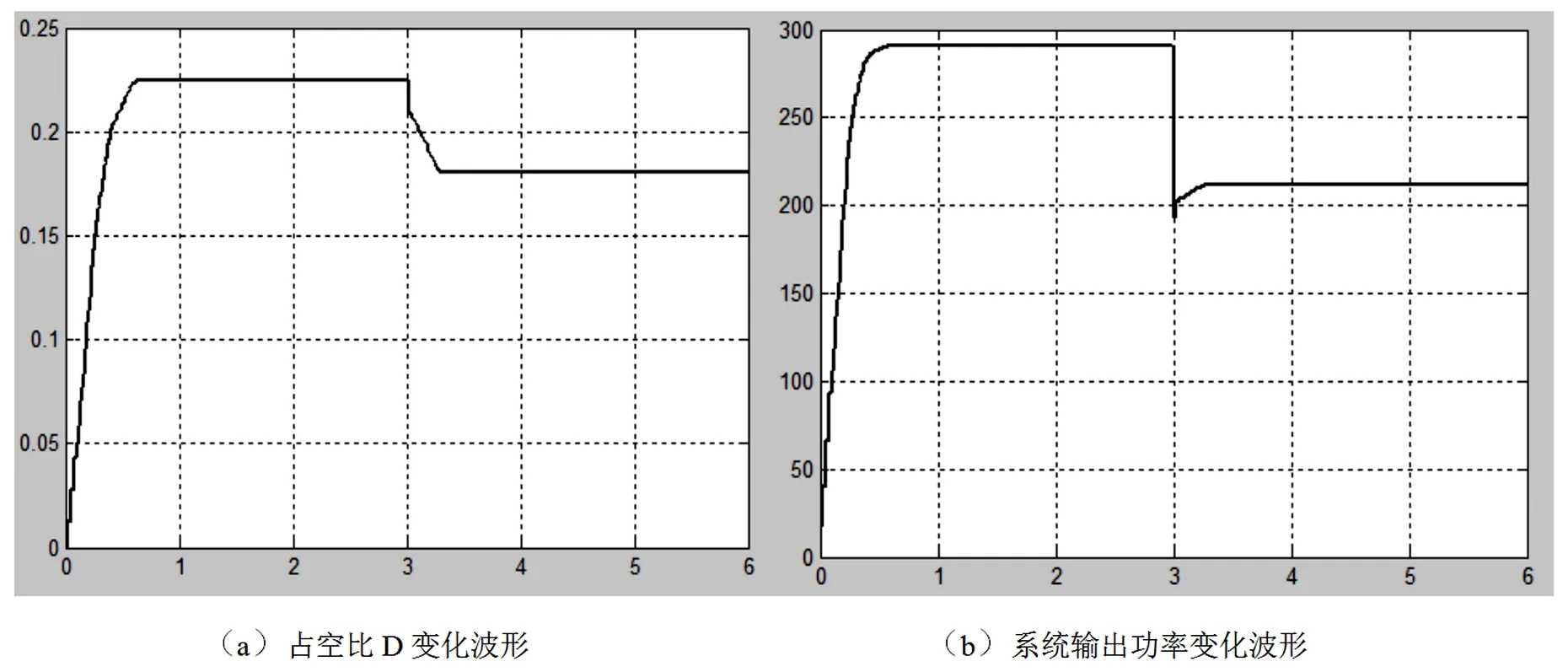
图9　系统光照从800 W/m2突然减小到600 W/m2系统仿真波形

6 结论

(1)研究以光伏系统的等效电路图推导出其等效数学模型，然后加以简化改进。建立了其在SIMULINK中的仿真模型，并利用此模型构造出基于模糊算法的光伏系统MPPT控制系统。

(2)设计改进的模糊控制器能够迅速地捕捉到光伏电池的最大功率点，并且在MPP处没有波动。

(3)无论是在光照突然增强还是光照突然减弱的情况，系统都能够快速稳定地再次捕捉到系统的最大功率点,且捕捉的最大功率点基本没有误差。

[1]赵庚申,王庆章,许盛之.最大功率点跟踪原理及实现方法的研究[J].太阳能学报,2006,27(10):997-1001.

[2]符江升,肖大帅,杨钦超.基于Matlab/Simulink的光伏电池仿真模型研究[J].光电子器件应用,2012,14(2):44-46.

[3]杨金孝,朱琳.基于Matlab/Simulink光伏电池模型的研究[J].现代电子技术,2011,34(24):192-198.

[4]郑建立,叶秋香.光伏电池最大功率跟踪器的模糊控制及其应用研究[D].上海：东华大学,2006.

[5]薛定宇.控制系统计算机辅助设计-MATLAB语言与应用 第二版[M].北京:清华大学出版社,2006:372-379.

Photovoltaic Cell Model and MPPT System Simulation with Fuzzy Algorithm Based on SIMULINK

JING Hui-cheng1, XU Laili1, LI Jing1, XUAN Zhao-yan2, ZHAO Xin3

(1. College of Electrical Engineering, North China University of Science and Technology,Tangshan Hebei 063009,China;2. College of Mechanical Engineering, North China University of Science and Technology, Tangshan Hebei 063009,China;3. Tangshan Toyoda Science and Technology Co., Ltd Tangshan Heibei 063009, China)

photovoltaic cell; simulation model; simulink; fuzzy algorithm; control rule

Based on the equivalent circuit diagram of photovoltaic battery, the equivalent mathematical model was derived, and carry on the improvement of simplified, and the simulation model of photovoltaic cells in simulink environment was established, the simulation results show that the input and output characteristics of photovoltaic cells could be shown by the model .Fuzzy algorithm was applied to the simulation model of photovoltaic battery and the control rule was improved, MPPT photovoltaic battery system simulation model was set up. Simulation results show that the MPPT system can rapidly MPP at the current conditions, and can quickly track MPP of the system again after environment mutation, and no fluctuation after the system is stable, it provides evidence for making effective MPPT photovoltaic controller.

TP273+.4

A