椭圆弧柔性铰链刚度简化计算及优化设计

付锦江，颜昌翔，刘　伟，袁　婷，2

(1.中国科学院 长春光学精密机械与物理研究所，吉林 长春 130033;2.中国科学院大学，北京 100039)



椭圆弧柔性铰链刚度简化计算及优化设计

付锦江1，2*，颜昌翔1，刘伟1，袁婷1，2

(1.中国科学院 长春光学精密机械与物理研究所，吉林 长春 130033;2.中国科学院大学，北京 100039)

本文主要研究了椭圆弧柔性铰链刚度的优化设计方法。首无，针对椭圆弧柔性铰链刚度计算公式过于复杂的问题，采用幂函数非线性曲线拟合的方法，推导了椭圆弧柔性铰链刚度的近似理论计算公式。然后，基于近似理论计算公式，分析了柔性铰链的精度特性及工作时的最大应力；采用GlobalSearch全域优化指令和Fmincon局域优化指令对椭圆弧柔性铰链工作方向的最大刚度进行了优化设计。最后，采用有限元仿真和实验验证的方法证实近似理论计算公式的适用性和优化结果的可靠性。验证显示：实验结果与近似理论计算结果的相对误差小于5%，表明提出的方法不仅省去了繁杂的有限元模型建立以及计算和修改的过程，大大提高了设计效率；而且通过优化计算可以得到椭圆弧柔性铰链的最大刚度。

椭圆弧柔性铰链；转动刚度；刚度计算；非线性曲线拟合；优化设计；有限元分析

1　引　言

柔性铰链在实际使用时集成在两个刚体之间，通过材料的弹性变形，作为旋转运动副而实现刚体运动的传递。因其具有加工简单、无机械摩擦、无间隙、高精度和免组装等优点而受到光学结构研究人员的重视，被广泛应用于精密机器人，装配及高精度位移平台，如柔性关节爬行机器人[1]，柔性探头微夹持器[2]，高精度、高速率的XY位移平台[3]和压电驱动位移平台[4]等领域。

影响柔性铰链工作性能的因素主要包括3个方面：刚度，运动行程和工作时的最大应力。国内外众多学者对柔性铰链准静态性能的研究较多，1965年，Paros和Weisbord[5]最早根据欧拉-伯努利梁理论推导出圆弧型柔性铰链柔度计算的精确和近似理论计算公式；Tseytlin[6]通过对圆弧型轮廓采用逆保角映射推导出了圆弧形柔性铰链刚度计算公式，与Paros和Weisbord推导的理论公式相比，其结果与实验结果的误差更小；Wu[7]在2004年推导出了相对简单又准确的圆弧型柔性铰链的刚度计算公式;LOBONTIU[8]等推导了抛物线和双曲线的柔度，精度及应力特性；RYU[9]等人分析了机械加工误差对柔性铰链性能的影响;Chen[10]等人在2014年通过有限元的方法得到了切口型柔性铰链的应力集中系数的经验计算公式。根据凹口曲线类型不同，柔性铰链又分为圆弧型，椭圆弧型，抛物线型，双曲线型，V型及其各种混合型等。SMITH[11]等人研究了椭圆弧柔性铰链的刚度计算式;Tian[12]等人研究了V型倒角柔性铰链等；近些年混合型柔性铰链的研究也比较多如：LOBONTIU等人研究了圆角抛物线混合型[13]，倒圆角直梁型[14];Lin[15]等人研究了一边为双曲线，另一边为倒圆角的混合不对称柔性铰链的性能；Chen[16]研究了椭圆弧倒角直梁柔性铰链。

目前国内外对柔性铰链的分析大多集中于柔度，精度及应力的分析，对柔性铰链的优化设计比较少：Chen[17]采用粒子群遗传算法对椭圆弧柔性铰链的柔度进行了优化；Bona等[18]和Zelenika等[19]都基于参数化有限元模型的方法分别对柔性机械进行了刚度优化设计和对柔性铰链进行了自由形状优化；2011年，北京理工大学的Xie[20]采用有限元方法进行了圆弧型柔性铰链的优化设计，优化后全柔性五杆机构的柔度增大，满足优化要求。

虽然SMITH和Chen等对椭圆弧柔性铰链都进行了研究，推导出了其刚度计算公式，但其计算公式都比较复杂，不利于椭圆弧柔性铰链的优化计算；目前柔性铰链的优化设计大多集中于柔性铰链的数值仿真计算，过程比较复杂，不利于工程应用。针对椭圆弧柔性铰链刚度计算公式过于复杂的问题，本文采用非线性曲线拟合的方法得出了椭圆弧柔性铰链工作方向刚度近似理论计算公式，进一步推导出了椭圆弧柔性铰链许用应力和精度的近似理论计算式；然后，综合考虑材料的许用应力和铰链的精度要求，采用Matlab软件进行椭圆弧柔性铰链工作方向最大刚度的优化设计；最后，通过有限元仿真和实验验证了近似理论计算公式的适用性和优化结果的准确性。借助于近似理论计算公式，采用Matlab进行刚度优化，大大提高了设计效率，省去了繁杂的有限元模型建立，计算和修改的过程，且通过优化计算可以得到椭圆弧柔性铰链最大刚度。

2　椭圆弧柔性铰链性能分析

2.1椭圆弧柔性铰链工作方向刚度

图1所示为弓形椭圆弧柔性铰链在z=0平面内的示意图，弓形圆心角为φmax， 左端固定，右端自由，长半轴为a，短半轴为b，宽度为w，最小切割厚度为t。

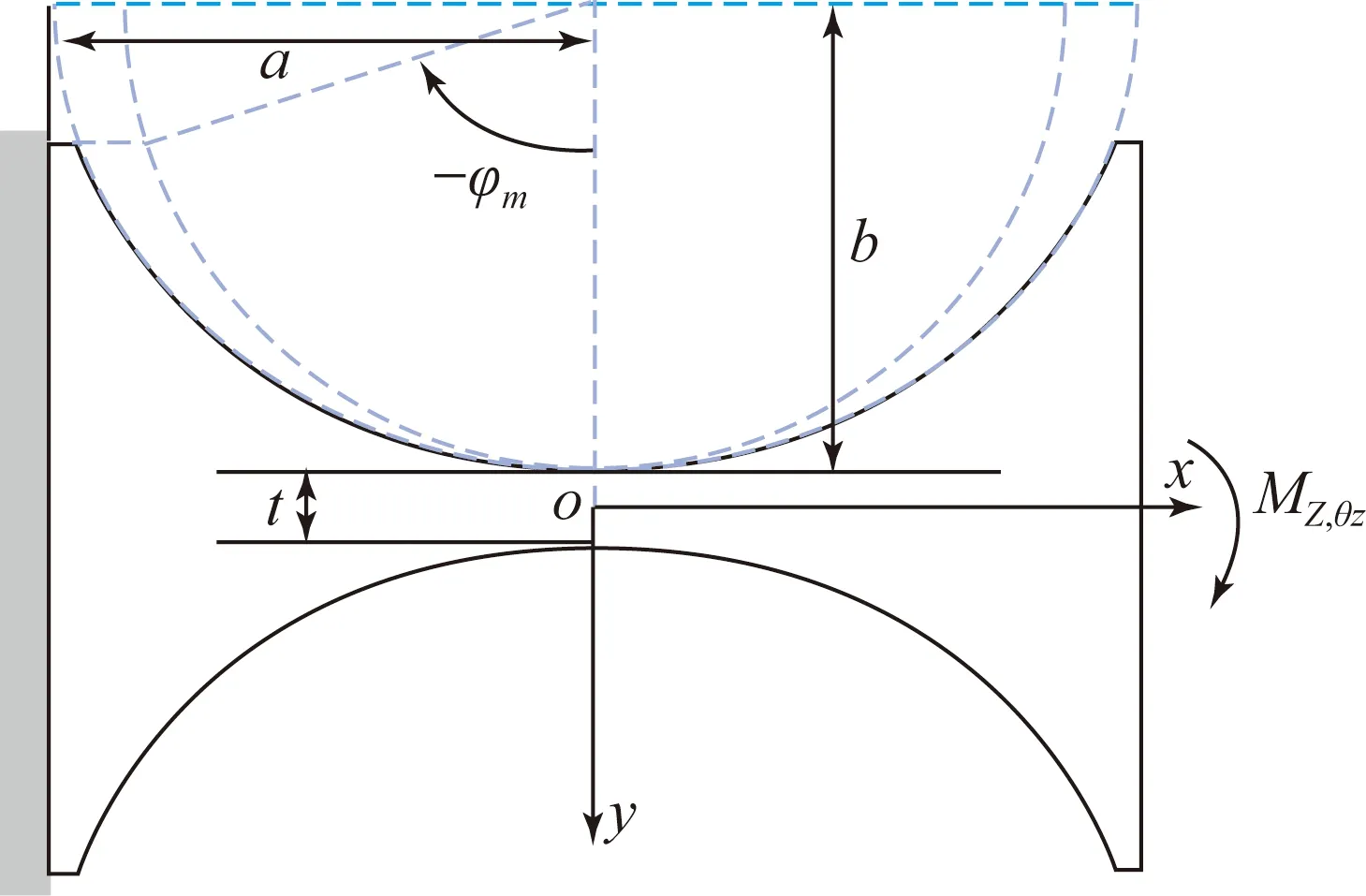
图1　椭圆弧柔性铰链参数及坐标系

z轴为柔性铰链的输入轴，当φm=π/2时，柔性铰链为正椭圆柔性铰链，根据文献[10]可知，式(1)是椭圆弧柔性铰链工作方向上转动刚度的理论计算公式，其计算比较准确，但过于复杂，不便于椭圆弧柔性铰链的优化设计：

令

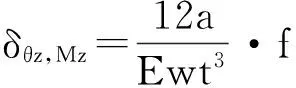
(1)

式中：a为椭圆弧柔性铰链的长半轴；w为椭圆弧柔性铰链的宽度；E为材料的弹性模量；t为柔性铰链的最小切割厚度；s=b/t，b为椭圆弧柔性铰链的短半轴；Kθz，Mz为柔性铰链准确计算的工作刚度。

2.2转动刚度近似理论计算公式的推导

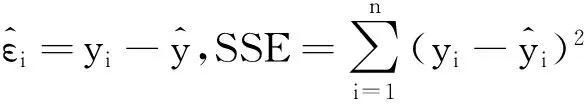
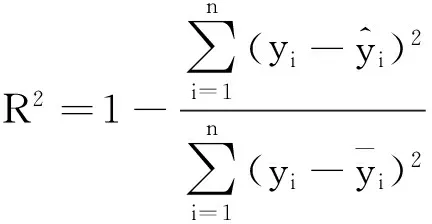
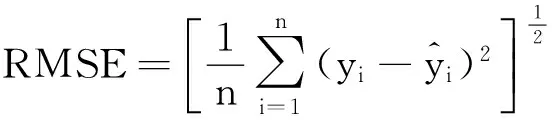
(2)

对f函数进行非线性拟合，拟合结果和残差分布如图2所示，分别进行了幂函数拟合，指数拟合，二次多项式拟合和三次多项式拟合。

图2　曲线拟合及残差分布图

由残差图分布可知，对f函数进行幂函数拟合所得结果最为合理，最大残差小于0.05。由图2可知：f函数采用幂函数拟合方式拟合效果最佳，拟合得到的函数为：

f′=msn=1.122s-0.485.

(3)

为使拟合函数更为简洁，取拟合函数系数m=1.15，n=-0.5，得到近似拟合函数：

f″=msn=1.15s-1/2.

(4)

图3所示为f函数曲线，拟合函数曲线 f″，残差曲线及近似拟合函数相对函数f的相对误差曲线，由图3可知，相对误差随着s的变化而变化，当s<2时，相对误差大于4%，当s>4时，相对误差小于1%，曲线拟合度好，近似拟合函数拟合优度评价参数结果如表1所示。

表1　函数拟合评价参数表

图3f函数及其拟合函数结果比较

Fig.3Contrastbetweenfunctionsfandf″

将式(4)代入式(1)，可得刚度近似理论为：

(5)

当a=b=R时，椭圆弧柔性铰链变成了圆弧型柔性铰链，则刚度近似理论为：

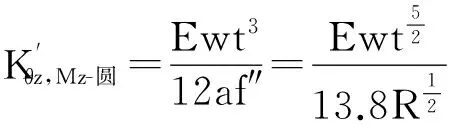
(6)

1965年由Paros和WEISBORD[14]推导出的圆弧型柔性铰链的简化公式为：

(7)

式(6)和(7)的区别只是系数的不同，系数的相对误差为2.4%，证明了椭圆弧柔性铰链的近似刚度理论计算公式的相对准确性。

2.3椭圆弧柔性铰链工作时最大应力分析

柔性铰链在最小切割厚度且距X轴最远处的抗弯截面模量最小，应力最大。考虑应力集中的影响，设应力集中系数为k，根据材料力学中纯弯曲理论可以得到最大应力计算式：

(8)

根据文献[10]，应力集中系数k的表达式为：

(9)

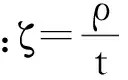
一般在设计时，往往只知道柔性铰链的偏转角度范围，材料的允许应力大小，偏转精度的要求而不知道其所需要的弯矩大小，所以假设设计的柔性铰链的最大偏转角为θ，则对应的弯矩为：

(10)

将式(9)，(10)代入式(8)可得铰链工作时最大应力和偏转角的关系：

(11)

将式(4)代入式(11)得椭圆弧柔性铰链的最大工作应力计算公式：

(12)

2.4柔性铰链的精度特性分析

一般将铰链中心点的位移作为铰链精度的分析指标[8]，柔性铰链中心点的位移其实也就是铰链在中心点处的挠度：

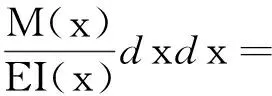
又

x=asinφ，dx=acosφdφ，h(φ)s=2b+t-2bcosφ，

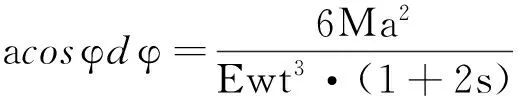
(13)

在铰链偏转角θ一定的情况下，将式(10)代入式(13)得：

(14)

3椭圆弧柔性铰链最大刚度优化设

计实例分析

3.1优化模型

椭圆弧柔性铰链的优化问题数学模型为：

fobj=max(Kθz,Mz)=min(-Kθz,Mz)=

令：

x1=a，x2=b,x3=t，x(x1,x2,x3)T，

(15)

为了提高椭圆弧柔性铰链的工作精度，a取值不宜过大，令椭圆弧的长半轴a<20mm， 由前面分析可知，当s>4时，近似理论计算公式相对误差比较小，所以20>a>b>4t>0，由此可得：线性不等式约束矩阵A= [-1 1 0;0 -1 4]，b= [0;0]，边界约束lb= [0;0;0]，ub=[20;20;5]。

非线性约束主要包括两部分：

(1)柔性铰链强度等式约束：根据式(12)，可得强度等式非线性约束条件为：

ceq(x)=Etθk-2.3as-1/2σymax=0.

(16)

(2)柔性铰链精度不等式约束：假设偏转角为10mrad，yc<10μm，根据式(14)可得不等式非线性约束条件为：

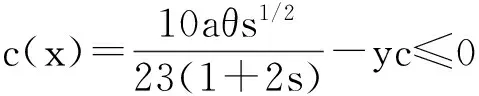
(17)

3.2优化方法及优化评价参数

优化可以看作是寻找函数最小值点的过程，最小值点又可以分为局域最小值点和全域最小值点，优化模型是一求解带约束多变量非线性目标函数的最小值，根据各优化指令的使用特点，最终选择了GlobalSearch实施的全域优化指令和Fmincon局域优化指令。

Fmincon优化结果的评价指标包括：目标函数值的变化趋势，约束冲突值(TolCon)和一阶优化系数(First-OrderOptimality)，对于同时具有等式约束和不等式约束的优化问题，一阶优化系数为：

minf(x),s.t.gj(x)≤0(j=1,2,…,m),

hk(x)=0(k=1,2,…,l.

对应的拉格日函数为：

L(x,λ)=f(x)s=∑λg,jgj(x)+∑λh,khk(x).

库恩-塔克条件可表述为：

xL(x,λ)=0，λg,jgj(x0=0，

‖xL(x,λ)‖=

‖f(x)∑λg,jgj(x)+∑λh,khk(x)‖∞，

(18)

‖λg,jgj(x)‖表示向量λg,jgj(x)的无穷范数，则一阶优化系数取‖xL(x,λ)‖和‖λg,jgj(x)‖中的较大值。

由式(18)可知：一阶优化系数代表了迭代过程中变量离变量最优值(目标函数取极小值时的变量)的远近程度，其值越小，代表迭代值越接近优化值，它是带约束目标函数取得极小值的必要非充分条件。

3.3优化结果

椭圆弧柔性铰链的优化参数如表2所示，采用Fmincon局部搜索优化得到了局部最佳变量值，目标值、约束值和一阶优化系数在优化迭代中的变化，如图4所示，目标函数随着迭代的增加而减小，满足优化的要求，最终目标函数局部最优值为-95.8N·m/rad，随着迭代的进行约束值和一阶优化系数都在不断的接近于0，最终经过6次迭代以后，约束值为0，一阶优化系数(First-OrderOptimality)为2.11×10-6，接近于0，说明局部优化结果可靠，最佳变量值为x=(10.35，7.008，1.752)即：a=10.35mm，b=7.008mm，t=1.752mm，将优化结果代入式(5)计算得：

计算结果与优化结果一致，说明理论计算和优化结果可靠。

表2　优化模型及有限元仿真参数

图4　局部优化结果

全局搜索优化结果如图5所示，全局优化目标函数最小值为-95.8N·m/rad，与局部优化结果一致。

图5　全局优化结果

4　有限元仿真和实验验证

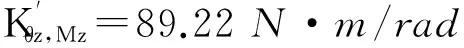
4.1有限元仿真

通过UG建立几何模型，Hypermesh建立有限元模型，有限元模型如图6所示，模型由3 870个单元组成，铰链部分网格单元比较密，左端完全固定，右端施加绕工作轴方向的弯矩，通过有限元仿真计算得到该柔性铰链的刚度为86.4N·m/rad，精度yc为9.98μm，应力σymax为156.6Mpa，仿真结果与近似理论计算结果误差分析如表3所示。

图6　柔性铰链有限元模型

刚度/(N·m/rad)精度/μm应力/Mpa有限元仿真结果86.49.98156.6近似理论计算结果89.29.84154.4有限元仿真与近似理论计算的相对误差/%3.14-1.42-1.42

由表3可知：仿真结果和近似理论计算结果的相对误差都小于4%，且精度和应力的相对误差小于2%，仿真结果满足优化模型的约束条件。

4.2工作刚度的实验验证

采用电火花线切割工艺加工了该柔性铰链并搭建实验来检测优化柔性铰链的工作刚度，实验原理如图7所示。主要包括一分辨率为0.2″的平行光管，优化柔性铰链，黏接在连接板上的反射镜，与柔性铰链固连的连接板和基座，基座又与光学平台固连，不同质量的砝码，细线和量块。通过细线穿过连接板的细孔在连接杆的一端施加力mg，用平行光管测量砝码施加前后反射镜的偏转角即柔性铰链的偏转角θ，实际的实验装置如图8所示。由此，椭圆弧柔性铰链的工作刚度计算公式为：

K实验=M/θ=mgLcosθ/θ，

(19)

式中：K实验是实验检测刚度(N·m/rad)；m是砝码的质量(g)；g为重力加速度(9.8m/s2)；L为常数(L=0.047 5m)；θ为偏转角(mrad)。

图7　柔性铰链刚度测试实验原理图

Fig.7Diagramofexperimentalarrangementforthecalculationforthestiffnessofnotchhinge

图8　刚度检测实验装置图

在实际实验时，砝码质量依次为10g，20g，50g，100g和200g。为了减少测量随机误差，不同力矩情况下实验进行了多次重复测量，偏转角取多次测量的平均值， 对实验结果进行数据处理，得到该优化柔性铰链的转角-弯矩曲线，如图9所示，曲线的斜率即为该优化柔性铰链的工作刚度K实验为93.47N·m/rad，实验结果与近似理论计算结果的相对误差为：

(20)

将实验刚度值和理论计算刚度值代入式(20)，得δ实验-近似理论=-4.76%。

图9　柔性铰链弯矩-转角拟合曲线

Fig.9Fittingcurveaboutthebendingmomentsandrotationanglesoftheoptimalelliptichinge

5　结　论

本文采用幂函数非线性曲线拟合方法，得出了椭圆弧柔性铰链工作刚度的近似理论计算公式，当s(b/t)>4时，近似理论计算公式和准确理论计算公式两者的相对误差不超过2%。将近似理论计算公式用于椭圆弧柔性铰链的优化设计，利用Matlab软件对某一椭圆弧柔性铰链的最大刚度进行了优化计算，优化结果与近似理论计算结果相一致。通过有限元仿真和实验验证了椭圆弧柔性铰链工作刚度近似计算公式的适用性和优化结果的可靠性。椭圆弧柔性铰链工作刚度的仿真值，实验值与近似理论计算结果的相对误差都小于5%。

[1]SEOTW，SITTIM.Tank-likemodule-basedclimbingrobotusingpassivecomplaintjoints[J]. IEEE/ASME Transactions on. Mechatronics.， 2013，18(1)：397-408.

[2]WASONJD，WENJT，DAGALSKISNG.Dextrousmanipulationofamicropartwithmultiplecompliantprobesthroughvisualforcefeed-back[C]. in Proc. IEEE Int. Conf. Robot. Autom.， Shanghai， 2011： 6991-6996.

[3]POLLITS，DONGJ.Developmentofahigh-bandwidthXYnanopo-sitioningstageforhigh-ratemicro-nonmanufacturing[J]. IEEE/ASME Transactions on. Mechatronics.， 2011，16(4)：724-733.

[4]BASHASHS，JALILIN.Robustadaptivecontrolofcoupledparallelpiezo-flexuralnano-positioningstages[J]. IEEE/ASME Transactions on. Mechatronics.， 2009，14(1)：11-20.

[5]PAROSJM，WEISBORDL.Howtodesignflexurehinges[J].Machine Design，1965，37(27)：151-156.

[6]TSEYTLINYM.Notchflexurehinges：aneffectivetheory[J]. Review of Scientific Instrument.， 2002，73(9)：3363-3368.

[7]WUYF，ZHOUZHY.Designcalculationsforflexurehinges[J].Review of Scientific Instrument， 2002， 73(8)：3101-3106.

[8]LOBONTIUN，PAINEJ，MALLEYE， et al..Parabolicandhyperbolicflexurehinges：flexibility，motionprecisionandstresscharacterizationbasedoncomplianceclosed-formequations[J]. Precision Engineering， 2002，26：183-192.

[9]RYUJW，GWEONDG.Erroranalysisofaflexurehingemechanisminducedbymachiningimperfection[J].Precision Engineering，1997， 21： 83-89.

[10]CHENGM，WANGJL，LIUXY.Generalizedequationsforestimatingstressconcentrationfactorsofvariousnotchflexurehinges[J].Journal of Mechanical Design，2014，136(1)： 1-8.

[11]SMITHST，BADAMIVG，DALEJS， et al..Ellipticalflexurehinges[J].Review of Scientific Instrument，1997，68(3)：1474-1483.

[12]TIANY，SHIRINZADEHB，ZHANGD.Closed-formcomplianceequationsoffilletedV-shapedflexurehingesforcompliantmechanismdesign[J].Precision Engineering.， 2010，34：408-418.

[13]LOBONTIUN，MATTC，PETERSENT.Planarcompliancesofsymmetricnotchflexurehinges：therightcircularlycorner-filletedparabolicdesign[J]. IEEE Transactions on Automation Science and Engineering，2014，11(1)：169-176.

[14]LOBONTIUN，PAINEJSN.Corner-filletedflexurehinges[J].Journal of Mechanical Design，2001，123(3)： 346-352.

[15]LINRZH，ZHANGXM，LONGXJ， et al..Hybridflexurehinges[J].Review of Scientific Instrument， 2013，84，085004.

[16]CHENGM，SHAOX，HUANGX.Elliptically-arc-filletflexurehinges：towardageneralizedmodelforcommonlyusedflexurehinges[J].ASME Journal of. Mechanical. Design，2011，133(081002).

[17]CHENGM，JIAJY，HANQ.Geometricalprofileoptimizationofellipticalflexurehingeusingamodifiedparticleswarmalgorithm[C]. Springer-Verlag Berlin Heidelberg，2005，3644：533-542.

[18]BONAFD，MUNTEANUMG.Optimizedflexuralhingesforcompliantmicro-mechanisms[J]. Analog Integrated Circuits and Signal Processing 44(2)(2005) 163-174.

[19]ZELENIKAS，MUNTEANUMG，BONAFD.Optimizedflexuralhingeshapesformicro-systemsandhigh-precisionapplications[J]. Mechanism and Machine Theory， 2009，44：1826-1839.

[20]XIEZY，QIULF，BIANXX， et al..Derivationoftheprecisecalculationformulaofcomplianceandoptimaldesignofcircularflexurehinge[C]. Proceedings of IEEE，2011.

付锦江(1988-)，男，江西高安人，博士研究生，2010年于武汉理工大学获得学士学位，主要从事光学精密机械设计及检测研究。E-mail：ytfjj17@tom.com

导师简介：

颜昌翔(1973-)，男，湖北洪湖人，研究员，2001年于中国科学院长春光学精密机械与物理研究所获得博士学位，主要从事空间光学遥感技术方面的研究。E-mail：yancx@ciomp.ac.cn

(版权所有未经许可不得转载)

Stiffness calculation and optimal design of elliptical flexure hinges

FU Jin-jiang1，2*， YAN Chang-xiang1，LIU Wei1，YUAN Ting1，2

(1.Changchun Institute of Optics， Fine Mechanics and Physics，Chinese Academy of Sciences， Changchun 130033， China；2. University of Chinese Academy of Sciences， Beijing 100049， China)

*Corresponding author， E-mail：ytfjj17@tom.com

Anoptimizationdesignmethodforellipticalflexurehingesisresearched.Asthetraditionalcalculationformulaforthestiffnessofellipticalflexurehingesismorecomplex,thispaperdeducesaapproximatetheoreticalformulabynonlinearfittingmethodwithpowerfunction.Basedontheapproximatetheoreticalformula,itanalyzestheprecisioncharacteristicsoftheflexurehingesandtheirmaximumstressesatworking.Then,theglobaloptimizationsolverGlobalSearchandlocaloptimizationsolverFminconareusedtodesignoptimallythemaximumstiffnessofanellipticalflexurehingeataworkingdirection.Finally,theapplicabilityoftheapproximatetheoreticalcalculationequationandtheaccuracyoftheoptimizationresultsareassessedbycomparisonwiththeresultsfromfiniteelementanalysisandexperimentaldata.Theresultsshowthattherelativeerrorsbetweenthefiniteelementsimulation,experimentaldataandtheapproximatetheoreticalcalculationforthestiffnessofelliptichingearewithin5%.Itconcludesthatthemethodavoidsestablishingthecomplexfiniteelementmodeandtheprocessesofcalculationandmodification,andgreatlyimprovesthedesignefficiency.Moreover,itcanobtainthemaximumstiffnessoftheellipticalflexurehingesbyoptimizationcalculation.

ellipticalflexurehinge;rotationstiffness;stiffnesscalculation;nonlinearcurvefitting;optimizationdesign;finiteelementanalysis

2015-11-12；

2015-12-15.

国家863高新技术发展资助(No.2011AA12A103)；中国地质调查局工作项目支持(No.1212011120227)

1004-924X(2016)07-1703-08

TH131

Adoi:10.3788/OPE.20162407.1703