六招破解幂的大小比较
王卉
六招破解幂的大小比较
王卉
教材第62页有这样一道题:

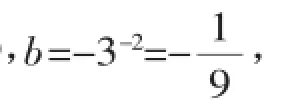
这是一道幂的大小比较题,是本章中常见题型,本题可通过幂的运算性质计算出结果,然后比较大小.这种方法可以归纳为:
第一招:直接计算法
然而,有时我们遇到的题目并不方便计算出结果,所以我们另外举例并总结了5种解决此类问题的方法,供同学们借鉴.
第二招:底数比较法
例2比较355、444、533的大小.
【分析】三个幂的指数都是11的整数倍,我们可以将指数化成相同,通过比较底数的大小,来确定三个幂的大小.
解:因为355=35×11=(35)11=24311,444=44×11= (44)11=25611,533=53×11=(53)11=12511,而125<243<256,所以533<355<444.
第三招:指数比较法
例3 若a=8131,b=2741,c=961,比较a、b、c的大小.
【分析】三个幂的底数都可以写成3n的形式,我们可以将底数化成相同,通过比较指数的大小,来确定幂的大小.
解:因为a=8131=(34)31=3124,b=2741=(33)41= 3123,c=961=(32)61=3122,而124>123>122,所以a>b>c.
第四招:乘方比较法
例4已知a3=5,b4=6,比较a、b的大小.
【分析】本题需要比较的是两个底数的大小,在指数和幂的值都不相同的情况下很难进行比较,所以我们需要将指数统一成12,通过比较幂的大小来确定底数的大小.
解:因为a12=(a3)4=54=625,b12=(b4)3=63= 216,而625>216,所以a12>b12,所以a>b.
第五招:差值比较法
【分析】作差比较法是比较两个数值大小最常用的方法,即对两值作差,看结果是正还是负,从而确定两值的大小.本题P和Q的分母相近,可先进行通分,然后求差值.
第六招:商值比较法
同样是例5,我们换个方法解答.
【分析】作商比较法是对两个数值作商,比较其结果与1的大小,从而确定两值的大小.本题中两式的分母为同底数幂,如果作商即可约分,方便用此法.
综上所述,我们在解题时,要细心观察题目的特征,根据题型特点灵活恰当地选择合适的解题方法.
(作者单位:江苏省泰州中学附属初级中学)

