如何轻松学好幂的运算

程芳



如何轻松学好幂的运算

程芳

幂的运算性质是整式运算的基础，也是中考必考点，在中考中着重考查基础知识的掌握和运用，以及对该性质的理解，题目不会很难，但是会有一定的综合性，应准确把握和理解幂的运算性质.本文从4个方面加以分析，供大家学习时参考.

一、清楚每个运算性质的由来

学习幂的运算性质时，要清楚每个运算性质的产生或推导过程，不要死记公式，否则性质易混淆出现错误.如a2·a3=a6，就是把同底数幂相乘和幂的乘方混淆了，如果结合推理过程来理解a2·a3，即2个a相乘与3个a相乘的积等于5个a相乘，则a2·a3=a5.只有真正理解了幂的运算性质的本质，解题时才不易出错.

二、明确幂的运算性质的相同点和不同点

相同点：①运算性质中的底数都不变，只是对指数进行运算.

②运算性质中的底数既可以表示具体的数，也可以表示整式.

③指数均为正整数.

不同点：结合公式.

am·an=am+n同底数幂的乘法：指数相加；

am÷an=am-n同底数幂的除法：指数相减；

（am）n=am×n幂的乘方：指数相乘；

（ab）m=am·bm积的乘方：等于各因数分别乘方的积.

另外am÷an=am-n中a≠0，其余公式中a可为任意实数.

三、注意幂的运算性质的拓展性

对于含有三个或三个以上同底数幂相乘（除）、幂（积）的乘方等运算，法则仍然适用.

例1计算：

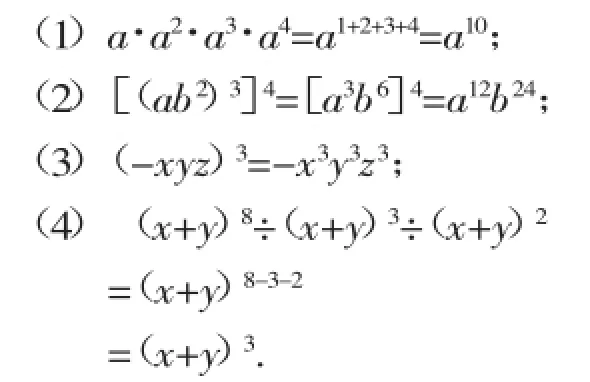
四、逆用幂的运算性质灵活解题

学习幂的运算性质，不仅要能从左到右运用性质计算，还要善于应用逆向思维，从右到左使用性质，巧用这种方法解决有关幂的问题，常可使问题得到简捷解决.

例2计算：

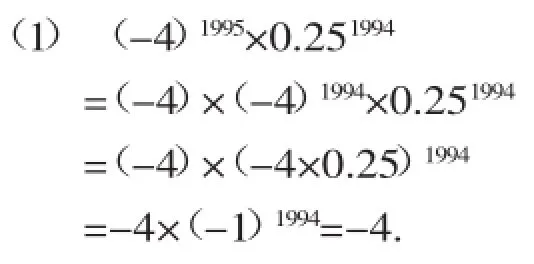
（2）已知10m=4，10n=5.求103m-2n+1的值.

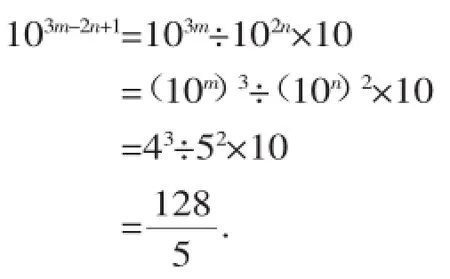
（作者单位：江苏省泰州市明珠实验学校）