浅谈幂的运算法则逆用

李爱华



浅谈幂的运算法则逆用

李爱华

同学们在学习“幂的运算”这一章时，不仅要熟练运用公式计算，还要会逆用这些公式进行计算.下面举几例来说明逆用公式在解题中的应用.

原公式逆用公式同底数幂的乘法：

同底数幂的除法：

（a≠0，m、n为正整数）

幂的乘方：

积的乘方：

一、求整数位数

例1 求n=212×58是几位整数.

【解析】可逆用上述幂的运算法则第1、4条，把n写成科学记数法a×10n的形式：

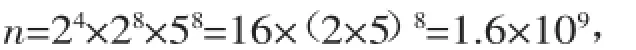
∴n是10位整数.

二、确定整数的末尾数字

例2 求7100-1的末尾数字.

【解析】先逆用幂的运算法则第三条，确定7100的末尾数字.

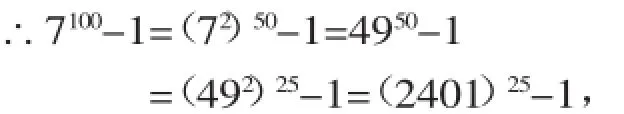
而（2401）25的个位数字是1，

∴7100-1的末尾数字是0.

三、比较两数大小

例3比较750与4825的大小.

【解析】750=（7）225=4925，可知前者大.

四、判断是否能整除

例4若3n+m能被10整除，你能说明3n+4+m也能被10整除吗？

【解析】若将3n+4+m变形成3n+m与10的整数倍的和的形式，此题就可迎刃而解.逆用幂的运算法则，有

3n+4+m=34×3n+m=81×3n+m=80×3n+3n+m，结论已明.

五、判定数的正、负

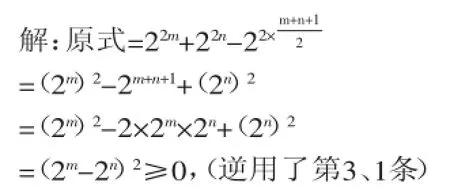
∴原数是非负的.

六、寻找除数

例6已知250-4能被60～70之间的两个整数整除，求这两个整数.

【解析】逆用幂的运算法则第一条将原数进行分解，就可找到解决此题的途径.

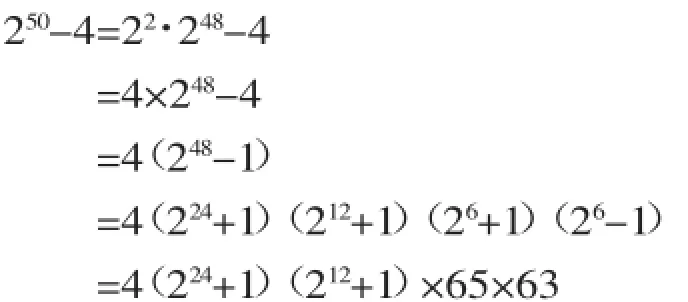
∴这两个数是65、63.

七、用于简便运算

例7计算：

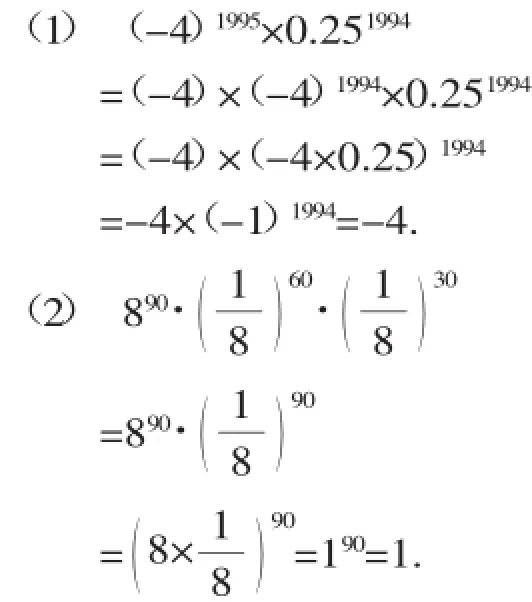
八、求代数式的值

例8已知10m=4，10n=5.求103m-2n+1的值.

【解析】逆用幂的运算法则.

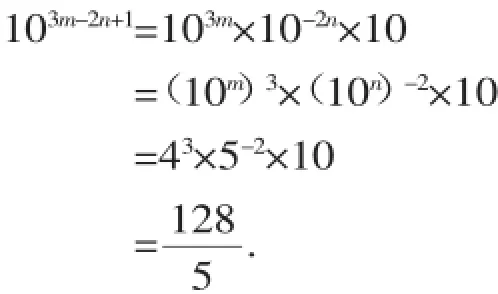
九、求参数

例9已知：2.54×210×0.1÷（5×106）=m× 10n（1≤m＜10）.求m、n的值.

【解析】逆用幂的运算法则，把等式的左边也转化成科学记数法的形式，便可求出m、n的值.

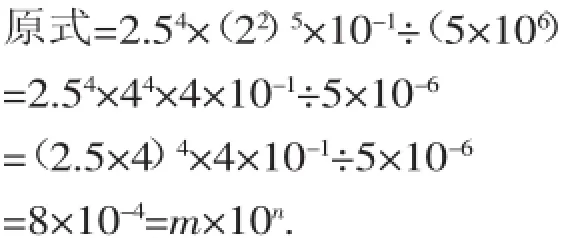
由科学记数法定义得m=8，n=-4.

实际上，逆用幂的这四条法则是一种常见的数学思想.同学们逆用幂的四条运算法则后，会发现那些原本看似束手无策的题目，前景也变得柳暗花明了.

（作者单位：江苏省泰州中学附属初级中学）