转子-定子耦合系统振动特性分析
李凯华,太兴宇,孙 丹,2
(1.沈阳鼓风机集团股份有限公司 研究院,沈阳 110142; 2.沈阳航空航天大学 辽宁省航空推进系统先进测试技术重点实验室,沈阳 110136)
转子-定子耦合系统振动特性分析
李凯华1,太兴宇1,孙丹1,2
(1.沈阳鼓风机集团股份有限公司 研究院,沈阳 110142; 2.沈阳航空航天大学 辽宁省航空推进系统先进测试技术重点实验室,沈阳 110136)
摘要:建立简化的双质点模型,对定子质量、支承刚度以及阻尼对系统振动响应的影响进行研究。分析发现,当定子的固有频率接近转子的固有频率时,导致转子的共振响应加剧;若定子的固有频率小于转子的固有频率,在转子的幅频曲线中定子的固有频率处会出现峰值,但转子的共振峰值会降低;适当地增加定子的支撑阻尼,可以有效抑制由定子共振导致的转子共振峰值增加的现象。对一个实际转子-定子系统采用有限元法对定子壁厚的影响进行了分析,得到了与简化模型相同的结论。
关键词:转子-定子耦合系统;共振峰值;固有频率;振动响应
旋转机械是工业部门中应用最为广泛的一类机械,在电力、能源、交通、石油化工以及国防领域都发挥着无可替代的作用[1-4]。而转子在运行过程中振动过大,往往会导致转子达不到工作转速,或者加速部件的损坏,同时也可能使转静件发生碰摩,有的甚至会引发严重的机毁人亡事故,造成重大的经济损失。以往对于转子振动特性的研究往往是建立转子-轴承系统动力学模型[5-9],只关注转子与支撑部件之间的联系。后来人们发现定子也会对转子的振动响应产生影响。陈果等[10-13]针对航空发动机整机振动分析,建立了转子-滚动轴承-机匣耦合动力学模型,并对其振动特性进行了分析。袁惠群[14]、周海仑等[15]建立了双转子-机匣耦合动力学系统,并对其发生碰摩时的故障特征进行了分析。 本文针对振动转子在运行过程中振动过大的现象,将转子-定子简化为双质点数学模型,研究了定子参数对转子振动响应的影响。最后针对一个实际电机模型,采用有限元法对定子壁厚的影响进行了研究,进一步分析了定子对转子振动特性的影响。
1 理论分析
根据待研究转子系统,将转子-定子耦合系统简化为如图1所示的双质点动力学模型。根据如图1所示模型,建立微分方程
(1)
其中,m1、m2分别为转子和定子质量;c1、c2分别为转子和定子弹簧阻尼;k1、k2分别为转子和定子支承刚度;F为激振力幅值;ω为激振频率;t为时间。为了分析定子对整体系统动力学响应的影响,现给系统设定参数列于表1,其中,工况1为定子质量的影响,工况2为定子支承刚度的影响。采用谐波平衡法对系统的响应进行求解[16]。
图2、图3为工况1时转子的振动响应。从图2中可以看到,随着m2的增加,定子的共振频率(fn2)逐渐减小,而转子的共振频率几乎不发生
变化;在m2较小时,几乎看不到定子的共振峰值,而当定子的共振频率接近或小于转子的共振频率时,定子的共振峰值开始变得比较突出。从图3中可以看到,当质量比在50附近时,即定子的共振频率接近转子的共振频率,转子的最大峰值达到最高点,而随着定子质量的继续增加,可以看到转子的最大峰值急剧降低,说明虽然在转子的幅频曲线中出现了定子的共振峰值,但也由于定子的振动吸收了一部分振动能量,使得转子的共振峰值降低。
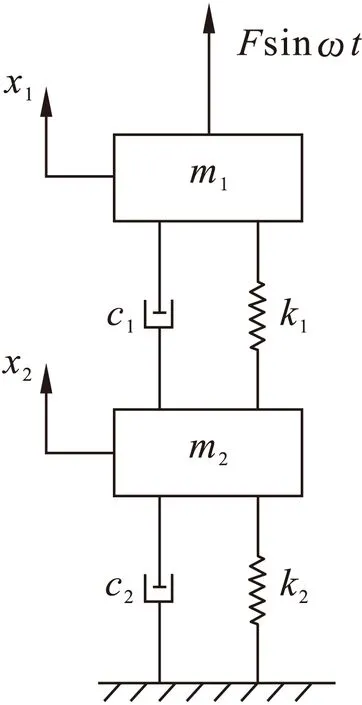
图1 双质点动力学模型
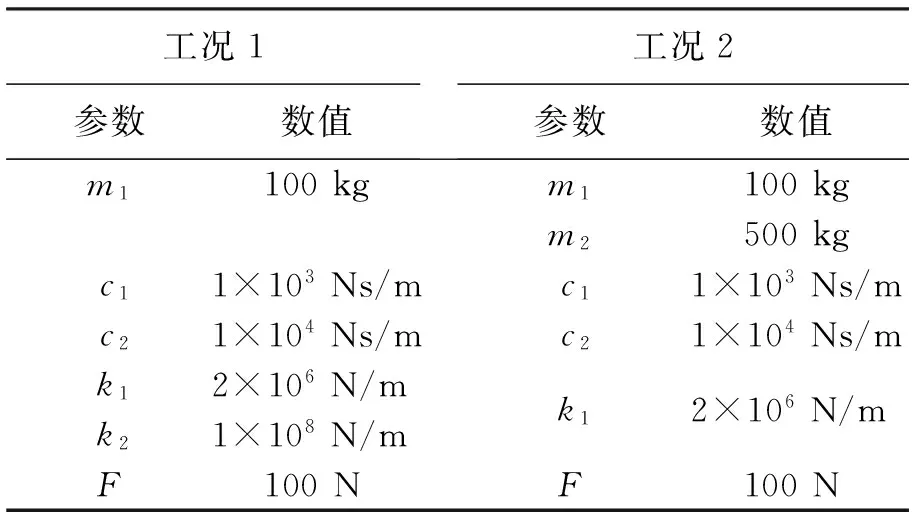
工况1参数数值工况2参数数值m1100kgm1100kgm2500kgc11×103Ns/mc11×103Ns/mc21×104Ns/mc21×104Ns/mk12×106N/mk12×106N/mk21×108N/mF100NF100N
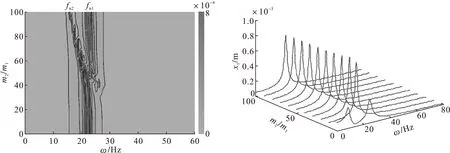
图2 工况1时的幅频曲线
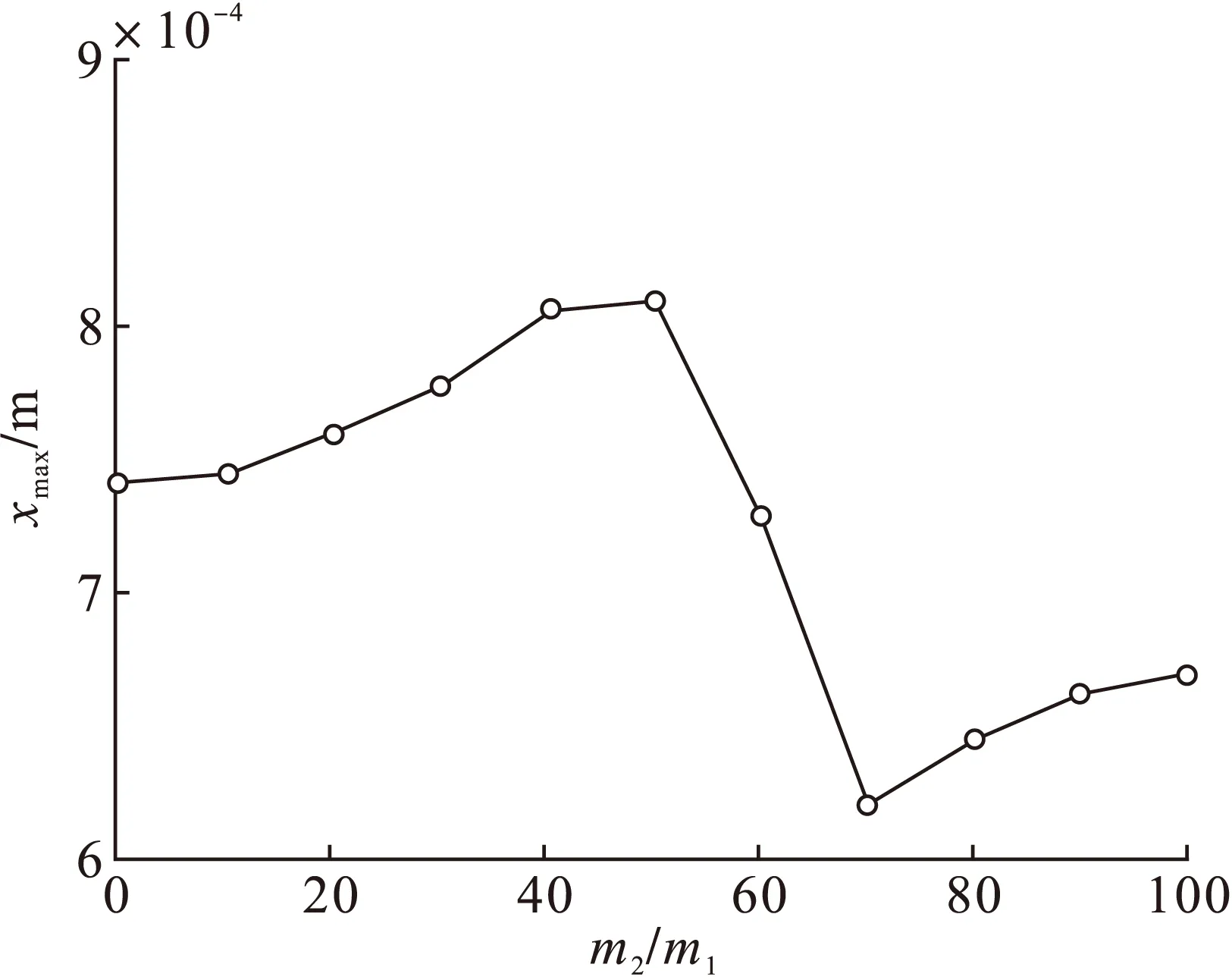
图3 m1最大幅值随质量比的变化曲线
图4、图5为工况2时转子的振动响应。从图2中可以看到,在定子支承刚度较低时,在转子的幅频曲线中出现了定子的共振峰值。但随着定子支承刚度的增加,谱图中只有转子的共振峰值,并且共振频率保持不变。从图5中可以看到,在刚度比较小时,转子的最大幅值出现了峰值,经过分析发现此处同样为定子频率接近转子频率处。
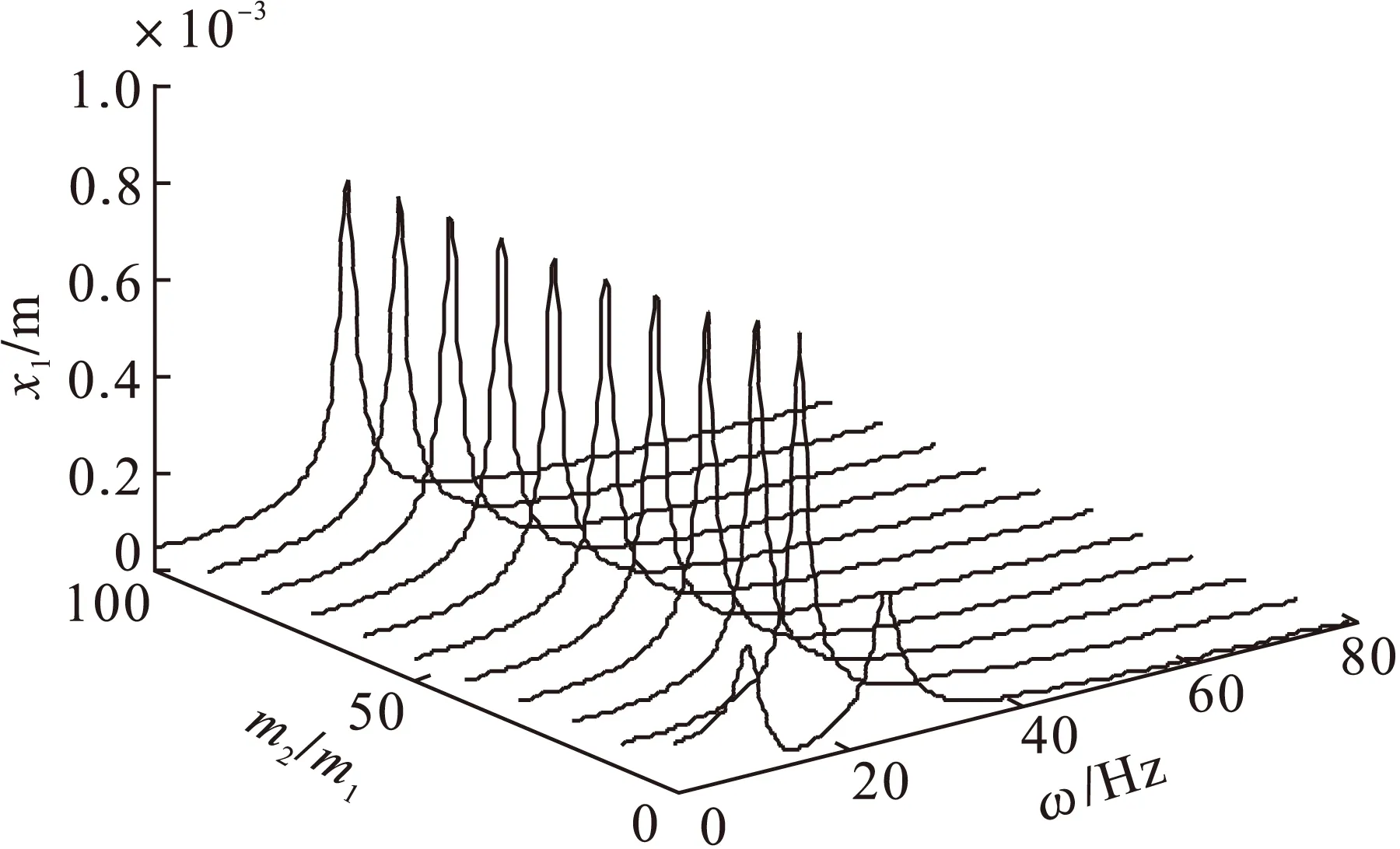
图4 工况2时m1的幅频曲线
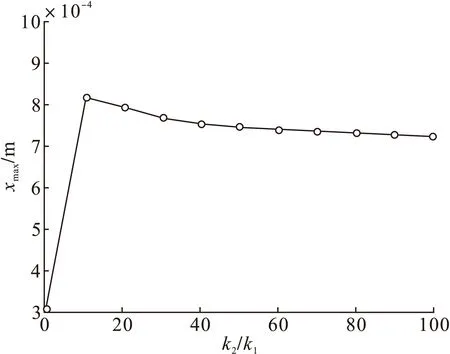
图5 m1最大幅值随刚度比的变化曲线
通过上面的分析可知,在定子共振频率接近转子共振频率时,会倒是转子的共振峰幅值增加,严重的话可能会导致设备无法超过1阶临界转速,达不到工作转速。分析其原因是由于定子的共振加剧了转子的共振幅度,为了阻止这种情况的发生,就需要抑制定子的共振峰值。图6为c2=1×105Ns/m增加了定子的支撑阻尼c2后的工况1时的m1最大幅值变化曲线。从图中可以看到,由于增加了定子的支撑阻尼,在图3中出现的峰值已经消失,说明定子的阻尼起到了很好的抑制作用。
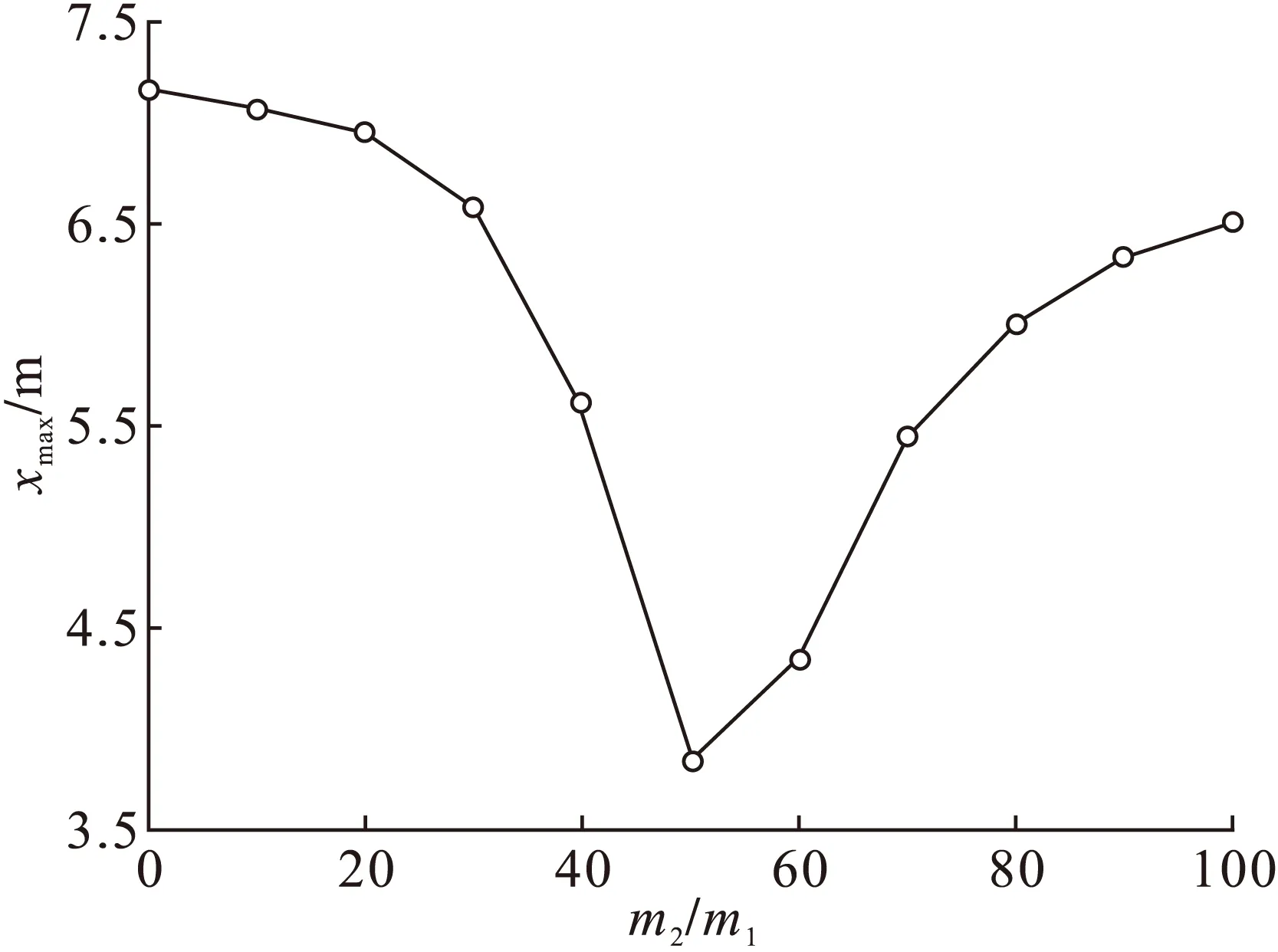
图6 m1最大幅值随质量比的变化曲线
图7为不同定子支承刚度下转子的振动幅值(非共振状态下的峰值)随质量比的变化曲线。从图中可以看到,在质量比为某一定值时,转子的振动幅值会发生一个突变,定子支承刚度越大,突变的位置越向后移。从整体上看,转子的振动位移是随着质量比的增加而减小,说明定子会吸收掉转子的一部分振动能量。
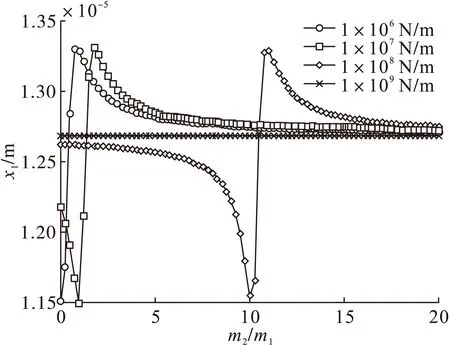
图7 ω=50 Hz时不同k2下m1随质量比的变化曲线
2 算例
下面对某厂生产的电机出现振动过大的问题采用有限元法进行分析。某厂生产的大型电机,在升速过程中,在某一频率开始产生较大振动,继续升速,振动达到最大值,并会出现倍频,达不到工作转速。经过一系列测试分析,得出定子质量太小是产生较大振动的主要原因。所以,我们对定子质量做了一些分析,考察定子质量对系统动力学特性的影响。
2.1模型建立
建立转子-定子-基础耦合有限元模型,如图8所示。图中,转子采用Beam188单元,转子和定子支撑采用Combi214弹簧,定子采用Shell183单元,基础采用Solid186单元。由于在实际生产过程中,定子与地基是用螺栓连接,方式比较固定,支承刚度设为1×108N/m,根据之前的分析,将阻尼设为1×105Ns/m。所以本节针对定子壁厚对振动响应的作用进行分析。
2.2定子对系统动力学特性的影响计算结果验证
(1)对固有频率的影响
表2为不同定子厚度下,系统的前6阶固有
频率。从表中可以看到,随定子厚度的变化,系统的固有频率几乎不发生变化。说明定子的质量对于转子的固有频率影响不大。
(2)对振动响应的影响
在ANSYS中,采用谐响应分析对定子的位移响应进行考察。在转子的中点施加不平衡力,然后进行谐响应分析,使用模态叠加法求解,因为要用到模态的参数,所以用谐响应分析之前,必须进行模态分析。频率范围选在包括一阶临界转速。取定子上的一点(节点10122)和转子上的一点(节点6)进行分析,如图9所示。查看在不同定子质量情况下,达到1阶临界转速时的峰值(表3和表4)。

图8 系统有限元模型

机壳厚度h/mm固有频率fn/Hz1阶2阶3阶4阶5阶6阶358.442162.61508.27613.241960.43446.51558.557163.03512.09613.731960.43446.53058.568163.10511.41613.811960.43446.5

图9 振动测点示意图
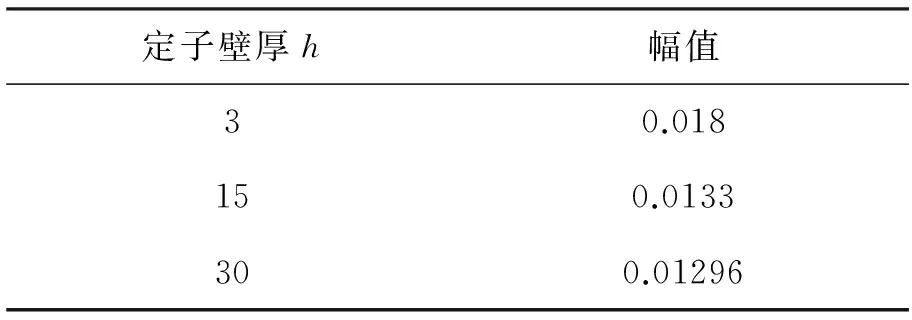
表3 不同定子质量下定子的幅值 mm
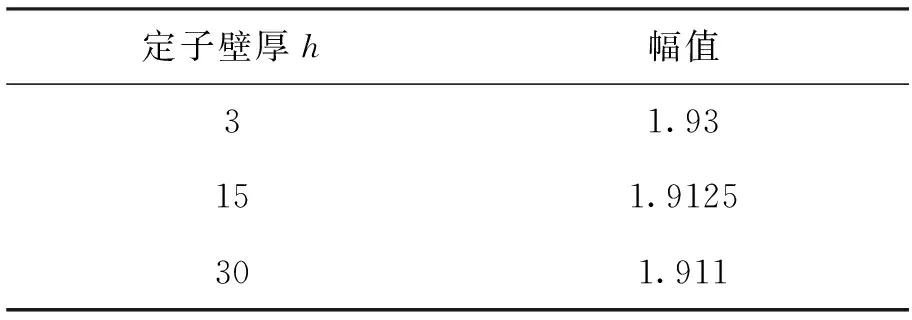
表4 不同定子质量下转子的幅值 mm
从表3和表4的结果中可以看到,在达到1阶临界转速时,定子的幅值和转子的幅值都随着定子壁厚的增加而减小,与之前分析的结论一致。说明在合适的支撑阻尼下,增加定子的壁厚可以在一定程度上减小系统的振动,吸收一部分振动能量。
3 结论
通过对解析模型的分析,讨论了定子质量和定子支承刚度以及阻尼对系统振动响应的影响。分析了在实际转子-定子-基础系统中,定子的质量对系统1阶临界处振动幅值的作用。经过分析得出以下结论:
(1)当定子的固有频率接近转子的固有频率时,会导致转子的共振响应加剧;若定子的固有频率小于转子的固有频率,在转子的幅频曲线中,在定子的固有频率处会出现峰值,但转子的共振峰值会降低;
(2)适当的增加定子的支撑阻尼,可以有效抑制由定子共振导致的转子共振峰值增加的现象;
(3)定子的质量对系统的固有频率影响不大,主要是通过改变支承刚度来调节系统的固有频率;
(4)在一定的支撑阻尼下,定子和转子的位移随着定子质量的增加而减小。
参考文献(References):
[1]闻邦椿.故障旋转机械非线性动力学近期研究综述[J].振动工程学报,2004,17(S):1-5.
[2]缪辉,王克明,翟学,等.反向旋转双转子系统动力学特性的有限元分析[J].沈阳航空航天大学学报,2011,28(4):27-32.
[3]孟宗,王亚超.基于微分局部均值分解的旋转机械故障诊断方法[J].机械工程学报,2014,50(11):101-107.
[4]王军锋,孙康.基于有限元法的转子临街转速计算[J].机械设计,2012,29(12):10-13.
[5]焦映厚,陈照波,刘福利,等.Jeffcott转子-可倾瓦轴承滑动轴承系统不平衡响应的非线性分析[J].中国电机工程学报,2004,24(12):228-232.
[6]O.DE SANTIAGO.L.S.ANDRES.Field methods for identification of bearing support parameters-part ii:identification from rotor dynamic response due to imbalances[J].Journal of Engineering for Gas Turbines and Power,2007,129(1):213-225.
[7]GUANGYAN SHEN,ZHONGHUI XIAO,WEN ZHANG,et al.Nonlinear behavior analysis of a rotor supported on fluid-film bearings[J].Journal of Vibration and Acoustics,2006(126):35-40.
[8]吕延军,虞烈,刘恒.椭圆轴承-转子系统非线性运动及稳定性分析[J].机械工程学报,2006,42(4):89-95.
[9]韩清凯,于涛,俞建成,等.单跨双圆盘不平衡转子-轴承系统的非线性动力学分析[J].机械工程学报,2004,40(4):16-20.
[10]陈果,李兴阳.航空发动机整机振动中的不平衡-不对中-碰磨耦合故障研究[J].航空动力学报,2009,24(10):2277-2284.
[11]陈果.航空发动机整机耦合动力学模型及振动分析[J].力学学报,2010,42(3):548-559.
[12]陈果.双转子航空发动机整机振动建模与分析[J].振动工程学报,2011,24(6):619-632.
[13]陈果.航空发动机整机振动耦合动力学模型及其验证[J].航空动力学报,2012,27(2):241-254.
[14]袁惠群,贺威韩,韩清凯.发动机双转子-机匣耦合系统碰摩故障分析[J].航空动力学报,2011,26(11):2401-2408.
[15]周海仑.含碰磨故障的航空发动机整机振动建模与分析[D].南京:南京航空航天大学,2009.
[16]XINGYU TAI,HUI MA,FUHAO LIU,et al.Stability and steady-state response analysis of a single rub-impact rotor system[J].Archive of Applied Mechanics,2015,85(1):133-148.
(责任编辑:宋丽萍英文审校:王云雁)
收稿日期:2015-07-20
基金项目:国家自然科学基金(项目编号:11302133);航空科学基金(项目编号:20140454003);辽宁省自然科学基金(项目编号:2015020113)
作者简介:李凯华(1983-),男,辽宁灯塔人,工程师,主要研究方向:转子动力学及旋转机械故障诊断,kaihua123@163.com。
文章编号:2095-1248(2016)02-0017-05
中图分类号:TN820.3
文献标志码:A
doi:10.3969/j.issn.2095-1248.2016.02.004
Vibration characteristics analysis of rotor-stator coupled systems
LI Kai-hua1,TAI Xing-yu1,SUN Dan1,2
(1.Institute,Shenyang Blower Works Group Co.Ltd,Shenyang 110142,China; 2.Liaoning Key Lab of Advanced Test Technology for Aerospace Propulsion System,Shenyang Aerospace University,Shenyang 110136,China)
Abstract:By establishing a simplified model of two mass points,the influence of stator quality,the support stiffness and damping on the vibration response of the system are analyzed in this paper.It has been found that when the natural frequency of the stator is close to the natural frequency of the rotor,the resonance response of the rotor is intensified.If the natural frequency of the stator is less than the natural frequency of the rotor,the peak value appears at the natural frequency of the stator,but the resonance peak of the rotor is reduced.Under the circumstance,the appropriate increase of the stator support damping effectively restrains the rise in the rotor resonance peak to the stator resonance.The influence of stator wall thickness is analyzed with the finite element method in a real rotor-stator system,and the same conclusion as the simplified model is obtained.
Key words:rotor-stator coupled systems;resonance peak;natural frequency;vibration response

