展现命题构想过程 分析解答引发反思———2015年宁夏中考压轴题的命制过程及反思

葛建华（宁夏教育厅教研室）施　巍（宁夏银川市兴庆区教育局教研室）

展现命题构想过程分析解答引发反思
———2015年宁夏中考压轴题的命制过程及反思

葛建华（宁夏教育厅教研室）
施巍（宁夏银川市兴庆区教育局教研室）

中考试题具有选拔、评价、引导，促进教学等功能.2015年宁夏中考压轴题将学生熟悉的一道宁夏中考试题适当取舍原有条件、添加新条件，以学生常用的三角板为背景尝试改编，把观察、探究、计算结合在一起，设置蕴含直角三角形、图形的旋转、线线平行、锐角三角函数、计算重叠图形面积及数形结合、化归转化等数学思想的阶梯型问题，通过不断尝试形成试题，达到考查学生基本数学素养的目的.

中考压轴题；命制过程；命题反思

根据《义务教育数学课程标准（2011年版）》（以下简称《标准（2011年版）》）的要求，中考试题既要注重考查学生数学基础知识与基本技能的理解和掌握，关注学生对数学思想方法和数学活动经验的理解情况的考查，又要突出考查学生的动手操作能力、创新意识.笔者参与命制了2015年宁夏中考试卷，将其中一道压轴题命制的心路历程和阅卷后的反思整理成文，与大家交流、分享.

一、素材选择

根据试卷双向细目表，所命制的试题为压轴题，应设计为以几何问题为背景，与动态探究相结合的综合性问题，把观察、探究、计算结合在一起，使其蕴含直角三角形、图形的旋转、线线平行、锐角三角函数、计算重叠图形面积等相关知识，以及数形结合、化归转化等数学思想.含30°，45°角的三角板是学生常用的学习工具，具有丰富的内涵，基于以上思考，以下面一道学生熟悉的宁夏中考试题为素材进行改编.

初稿：（2012年宁夏卷）如图1，正方形ABCD的边长为3，E，F分别是AB，BC边上的点，且∠EDF= 45°.将△DAE绕点D逆时针旋转90°，得到△DCM.

（1）求证：EF=FM；

（2）当AE=1时，求EF的长．

图1

二、试题改编过程

由题意，根据旋转的性质，知△DAE≌△DCM.得其对应边互相垂直，且AD∥CM，AE∥DC.当∠ADE= 30°时，∠AED=60°.若将Rt△DAE看成是一个含30°，60°角的三角板，因为∠ADC=90°，将点D看成是另一个含30°，60°角的三角板的直角顶点，舍掉其他条件，以点D为旋转中心，逆时针旋转Rt△DAE（看成含30°，60°角的三角板），旋转过程中随着旋转角的增大，旋转的三角板与Rt△DCM（看成含30°，60°角的三角板）重叠部分由无到有，与另一个可看成以点D为直角顶点、以DC为长直角边的三角板重叠部分由少变多，重叠部分图形的形状随之发生变化，重叠部分图形的面积随之发生变化，两三角板没有公共点的两边的位置关系也随之发生变化.根据函数的定义，两三角板重叠部分图形的面积是旋转角的函数，且是三角函数，因为学生在初中阶段只学习过特殊角（30°，45°，60°）的三角函数，因此两三角板重叠部分图形的面积与旋转角的函数关系不能作为考查对象.旋转过程中两三角板没有公共点的两边所在直线的位置关系有相交和平行两种，且按逆时针方向旋转30°时两三角板没有公共点的两边所在的直线平行（如图2）.在三角板中，特殊角除了直角，30°角外，还有45°，60°角，考虑到按逆时针方向旋转30°时，边A1C1到AB的距离较大，以及旋转到45°，60°时，两三角板重叠部分的形状都是三角形，因而将点B1与点C重合改为点A1与点C重合，得到如下改编.

图2

改编1：已知Rt△ABC与Rt△A1B1C1是全等的三角板，且∠A=∠A1=60°，∠C=∠C1=90°，点A1与点C重合，A1C1与CA重合.将三角板A1B1C1绕点C按逆时针方向旋转时AB与A1C1的交点为点M（如图3）.

（1）如图4，若将Rt△A1B1C1绕点C按逆时针方向旋转30°时，求证：B1C1∥AB；

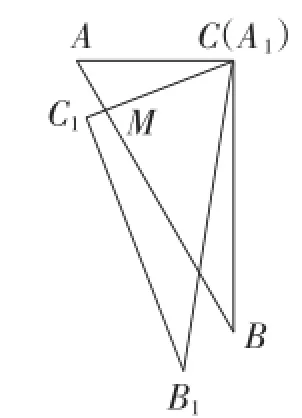
图3

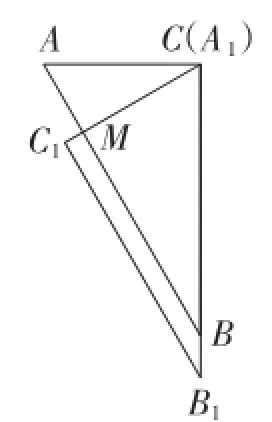
图4

思考：若Rt△A1B1C1绕点C按逆时针方向旋转60°，点C1恰好落在边AB上，设BC与B1C1的交点为点N，三角板重叠部分是△CC1N，点N将BC分为CN 与BN两部分（如图5）.若将Rt△A1B1C1绕点C按逆时针方向旋转45°时，设BC与B1C1的交点为点N，两三角板重叠部分是四边形CMQN（如图6），求四边形CMQN需转化为三角形的面积计算问题；按照由易到难的原则，第（2）小题设计为求旋转60°时两三角板重叠部分图形的面积，第（3）小题设计为求旋转45°时两三角板重叠部分图形的面积.

图5

图6

（2）如图5，若Rt△A1B1C1绕点C按逆时针方向旋转60°，点C1恰好落在边AB上，设BC与B1C1的交点为点N.求①CN与BN的比值；②两三角板重叠部分△CC1N的面积；

（3）如图6，若将Rt△A1B1C1绕点C按逆时针方向旋转45°.设BC与B1C1的交点为点N，A，C与AB的交点为点M，求四边形CMQN的面积.

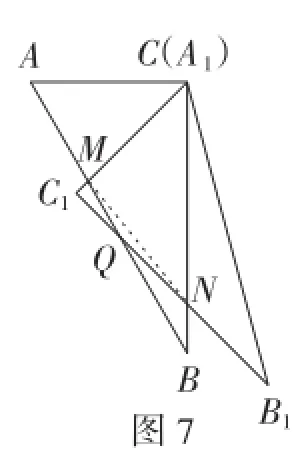
图7

【说明】对于第（3）小题，如图7，连接MN，考虑到四边形MQNC的面积可转化为△CC1N的面积与△MC1Q的面积的差计算时，△MC1Q图形较小；转化为△MQN的面积与△CMN的面积和计算时，△MQN图形较小，不利于学生借助几何直观解决问题.再则，利用完全相同的两个含30°，60°角的三角板呈现问题，一副三角板间的固有关系（如含45°，45°角三角板的斜边长与含30°，60°角三角板的长直角边长相等）没能体现出来，因而将两个完全相同的含30°，60°角的三角板呈现的问题改编成以一副三角板呈现的问题，改编如下.

改编2：如图8，是一副学生所使用的三角板，在△ABC中，∠C=90°，∠A=60°，∠B=30°；在△A1B1C1中，∠C1=90°，∠A1=45°，∠B1=45°，且A1B1=CB.若将边A1C1与边CA重合，其中点A1与点C重合．将三角板A1B1C1绕点C（A1）按逆时针方向旋转，旋转过的角为α，旋转过程中边A1C1与边AB的交点为点M，设AC=a.

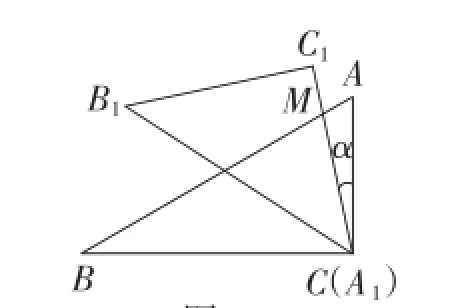
图8

（1）当α=30°时，证明：B1C1∥AB；

思考：若将三角板A1B1C1绕点C按逆时针方向旋转45°时，三角板A1B1C1的斜边A1B1与三角板ABC的直角边BC恰好重合，第（2）小题改变为如下形式.

解：（1）证明：如图9，当α=30°时，∠ACC1=30°.

因为∠A=60°，

所以∠AMC=90°，即CC1⊥AB.

因为CC1⊥B1C1，

所以B1C1∥AB.

图9

图10

（2）如图10，当α=45°时，B1A1恰好与BC重合，过点C作CH⊥AB于点H，

在Rt△CMH中，∠MCH=45°-30°=15°，

在Rt△ABC中，因为AC=a，∠A=60°，

所以A1B1=BC=

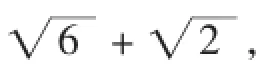
求两三角板重叠部分图形的面积需计算出B1C1的长，考虑到将含30°，60°角的三角板ABC中AC的长转化到含45°角的三角板A1B1C1中计算B1C1的长，对部分学生来说有困难.为了降低难度，在改编2的第（1）小题前面增加“计算A1C1的长”.作为第（1）小题，为计算两三角板重叠部分图形的面积做铺垫.考虑到三角板中出现的角（除90°角外）有30°，45°，60°角，当α=45°时，求的是三角形的面积；当α= 60°时，求的是四边形的面积.四边形的面积需化归转化为两个三角形面积的差或两个三角形面积的和来计算，考查化归转化的思想，因此在改编2的第（2）小题后又增加了“当α=60°时，用含a的代数式表示两个三角板重叠部分图形的面积”作为第（4）小题，最后做下定稿.

定稿：如图11，是一副学生用的三角板，在△ABC中，∠C=90°，∠A=60°，∠B=30°；在△A1B1C1中，∠C1=90°，∠A1=45°，∠B1=45°，且A1B1=CB.若将边A1C1与边CA重合，其中点A1与点C重合．将三角板A1B1C1绕点C（A1）按逆时针方向旋转，旋转过的角为α，旋转过程中边A1C1与边AB的交点为点M，设AC=a.

图11

（1）计算A1C1的长；

（2）当α=30°时，证明：B1C1∥AB；

（4）当α=60°时，用含a的代数式表示两个三角板重叠部分图形的面积.

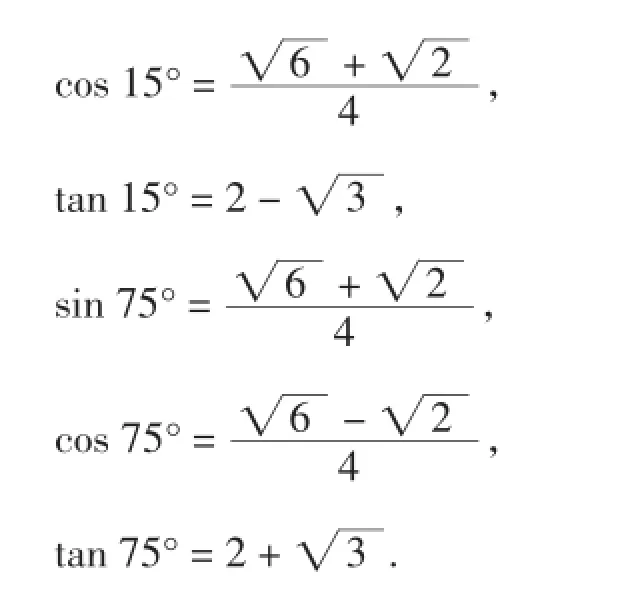
解：（1）在Rt△ABC中，

因为 AC=a，∠A=60°，

所以A1B1=BC=在Rt△A1B1C1中，

（2）略.

（3）略.

（4）当α=60°时，A1M=AC=a．

如图12，设B1C1分别与AB，BC交于点N，Q.

图12

所以S四边形CMNQ

【说明】由于一副三角板中A1C1的长度与AC的长度有内在的联系，其边B1C1与边AB平行是在旋转过程中出现的，因而将求A1C1的长定为第（1）小题，将证明B1C1∥AB定为第（2）小题.第（1）小题中计算A1C1的长，为第（3）小题、第（4）小题计算重叠部分图形面积做铺垫，第（3）小题为第（4）小题化归转化做铺垫.第（4）小题求四边形的面积化归转化为求两个三角形面积的差或两个三角形面积的和计算，因求解过程中运算量较大，求代数式的值已在第（3）小题中考查过，因而只要求学生用含a的代数式表示两个三角板重叠部分图形的面积.

答题卡中第（2），（3），（4）小题均给出了一个含30°，60°角的直角三角形，考查学生根据题意画图，数形结合分析问题、解决问题的能力.

基于以上改编过程中的思考，将该题设置为四道小题，并确定了先后呈现的顺序，但仍存在不尽人意之处，即宁夏中考压轴题一般设置为三问，该题设置为四问，第（1）小题与第（3）小题和第（4）小题、第（2）小题与第（3）小题、第（3）小题与第（4）小题之间有内在的联系，但第（1）小题与第（2）小题之间的内在联系较少.

三、阅卷反馈

1.别样解答

分析：第（1）小题略.第（2）小题在阅卷过程中，可以看出学生思维灵活，证明两直线平行的途径多样，如通过同位角相等、内错角相等、同旁内角互补证两直线平行，根据垂直于同一直线的两直线平行证两直线平行.第（3）、（4）小题从学生解答过程看，学生做辅助线的方法多样，计算路径多，不乏精彩之处.

解：（1）略.

（2）略.

（3）（方法1）如图13，过点M作MD⊥BC于点D.

设MD=x，

因为∠MCD=∠DMC=45°，所以DC=MD=x.

在Rt△BMD中，

∠BMD=90°-30°=60°，

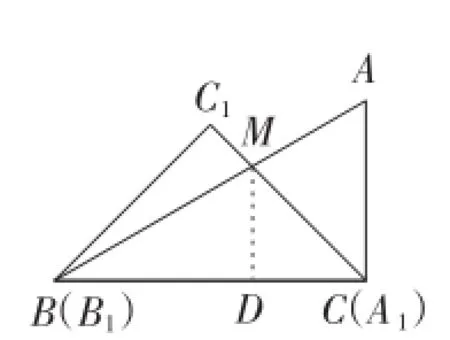
图13

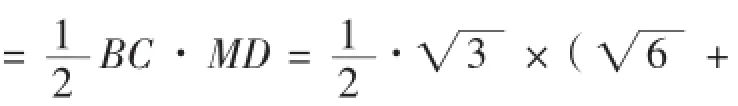
【评析】在两三角板重叠部分图形（△CMB）内作高MD，点D将线段BC分成线段BD和DC，根据BD+

（方法2）因为 ∠ABC=30°，∠C1BC=45°，

所以∠C1BM=15°（如图14）.

在Rt△BC1M中，

图14

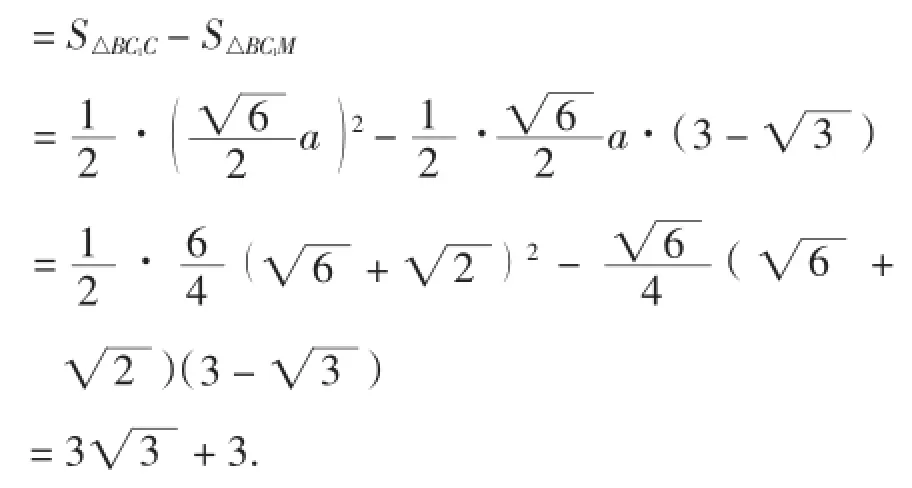
【评析】 方法2转化为计算△A1B1C1的面积与Rt△BC1M的面积的差，△A1B1C1两直角边长在第（1）小题中已求出，关键是求出MC1的值.

（方法3）如图15，过点M作MD⊥AC于点D.

图15

设MD=x，

则DC=MD=x.

因为∠A=60°，

所以∠AMD=30°.

【评析】方法3转化为计算△ABC的面积与△AMC面积的差，△ABC中BC的值在第（1）小题中已求出；在△AMC内作高MD，建立关于MD的方程，求得MD的值后，进而可求出两三角形面积的差.求出MD的值部分学生未化简，所以在求△MBC的面积时增加了计算量.

除了上述方法，还有学生根据如图10所示的S△CMB=BM·CH求重叠部分面积.

（4）（方法1）如图16，当α=60°时，CM=AC=a.

设B1C1分别与AB，BC交于点N，Q.

图16

图17

（方法2）当α=60°时，CM=AC=a，

设B1C1分别与AB，BC交于点N，Q.

如图17，在△CMB中，∠MCB=∠B=30°.过点M作MD⊥BC于点D，

在Rt△CC1Q中，∠CQC1=90°-30°=60°.

所以∠BNQ=60°-30°=30°.

因为∠B=30°，

过点N作NE⊥BC于点E，

【评析】方法1转化为△A1B1C1的面积与另外两个三角形面积的差的计算，运算量较大；方法2转化为两个三角形面积的差的计算，共作了两条辅助线.作辅助线对学生而言是个难点，能够作出两条辅助线解题，可见学生思维之缜密.

除了上述方法外，还有学生根据S四边形A1MNQ=S△ABCS△AMC-S△NBQ求重叠部分图形面积.

2.学生解答中出现的典型错误

阅卷过程中，可以看出学生思维灵活，看到多样的解题方法，但也有令人惋惜之处．

（3）推理论证不缜密.例如，证明两直线平行，写出的角多，但找不出判断两直线平行的条件.

（4）数形结合的意识不强.例如，将Rt△A1B1C1旋转60°时，画图忽视了A1B1=CB的条件，旋转后点B落在了Rt△A1B1C1内，或点B在Rt△A1B1C1的边B1C1上.

3.命题反思

从学生解答情况来看，压轴题入口要宽，应关注不同水平的学生，有梯度地、环环相扣地设置问题，让学生易于进入解题状态，尽可能地展现自己的数学才能，有效区分学生的解题能力和思维深度.解题过程中应适当控制运算量，关注解题方法的多样化，让学生在探究过程中选择适合自己的方法解题.

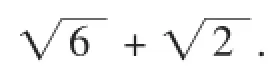
命制以几何问题为背景，与图形的旋转、锐角三角函数、图形的面积相结合的几何计算（论证）型中考压轴题，首先，要对命题的形式、结构，考查的知识点、运算技能、数学思想和方法，逐次递进的梯度、难度系数仔细斟酌.其次，要选择一道良好的试题作为素材，适当取舍原有条件、添加新条件，设置循序渐进的问题，通过不断尝试形成试题.最后，要精心打磨，杜绝歧义，使之体现命题方向，体现教学导向.命制出高质量、评价导向功能好、学生收益面大的精彩试题是命题者不懈追求的目标.

［1］葛建华，施巍.2014年宁夏中考压轴题的命制过程及反思［J］.中国数学教育（初中版），2015（5）：32-36.

［2］桂文通.好题多磨，磨出精彩［J］.中学数学数学参考，2015（1/2）：114-116.

葛建华（1962—），男，中学高级教师，主要从事中学数学教学和命题研究.

2016—02—09

全国教育科学“十二五”规划2013年度教育部规划课题——提高中学数学课堂教学质量策略研究（FHB130491）.