浅谈分式的约分与通分

罗成群（贵州省瓮安县中坪中学）

浅谈分式的约分与通分

罗成群
（贵州省瓮安县中坪中学）

分式的约分与通分是人教版八年级下册第十六章——16.1.2分式的基本性质的后继学习内容。分式的约分与通分是学习分式运算的奠基石，也是学习解分式方程的基础。但这一知识点教科书讲解得简略，许多学生学习时都感到困难，为了帮助学生学习这一知识点以及加深学生对该知识点的认识，我对分式的约分与通分作如下解析：

一、分式的约分

1.理解分式约分的定义

与分数的约分类似，利用分式的基本性质，约去分式的分子和分母的公因式，不改变分式的值，像这样的分式变形叫做分式的约分。如分式约去分子和分母的公因式2x2y2，使化为就叫把分式约分。

分式的分子和分母都含有的因式叫做分子和分母的公因式。例如，分式，其中2x2y2叫做分式的分子和分母的公因式。

注意：

①分式的约分，一般要约去分子和分母所有的公因式，使所得结果成为最简分式或整式（单项式与多项式统称为整式）。

②分式约分的关键是确定分式的分子与分母的公因式。

③公因式的系数是分子与分母的系数的最大公约数；公因式的因式是分子与分母都含有的因式的最低次幂。

④分式约分的目的是把复杂的分式化成最简分数。

2.约分的方法和步骤

当分式的分子与分母都是单项式时，先找出分子与分母的公因式，然后约去分子与分母的公因式。

例如，约分：

二、分式的通分

1.理解分式通分的定义

与分数的通分类似，利用分式的基本性质，使分式的分子和分母同乘以适当的整式，不改变分式的值，把异分母的分式化成分母相同的分式，这样的分式变形叫做分式的通分。如把和化成分母相同的分式就叫把分式和通分，18a2b叫做分式和的最简公分母。

注意：

①分式通分的关键是确定各分式的最简公分母。

②分式通分的目的是把异分母的分式化成同分母的分式。

2.确定最简公分母的一般步骤

①最简公分母的系数是各分母系数的最小公倍数。

②最简公分母的因式是各分母所有因式的最高次幂（相同的因式取次数最高的一个）。

3.分式通分的一般步骤

①当各分式的分母都是单项式时，首先确定各分式的最简公分母，再利用分式的基本性质，把分式的分子与分母同乘以一个适当的整式，不改变分式的值，使各分式的分母化成最简公分母。

解：最简公分母是36a2b；

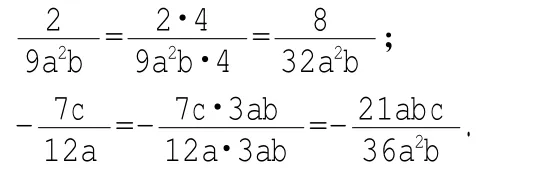
②当各分式的分母是多项式时，分式的分母能分解因式的一定要先分解因式，再确定各分式的最简公分母，再利用分式的基本性质，把每个分式的分子与分母乘以同一个适当的整式，不改变分式的值，使各分式的分母化成最简公分母。

例如，通分

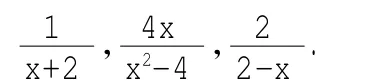
∴最简公分母是（x+2）（x-2）.

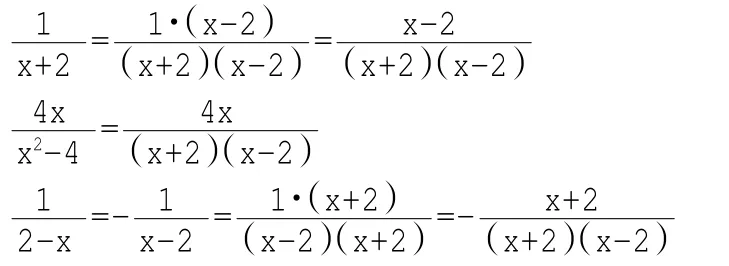
三、分式的约分与通分的联系与区别

1.联系

分式的约分与通分根据都是分式的基本性质。

2.区别

分式的约分是把分式的分子和分母都同除以一个不为零的整式，使分式的值不变，把复杂的分式化成最简分式；分式的通分是把分式的分子与分母都同乘以一个不为零的整式，使分式的值不变，把简单的分式化成复杂的分式。

四、分式约分与通分的焦点与难点：对多项式进行因式分解

1.对多项式进行因式分解的一般步骤：一提二套三分组

也就是说：对多项式进行因式分解时，多项式的各项有公因式的，一定要先提公因式，再看分解所得的因式还能不能套用公式（因式分解的平方差公式、完全平方公式等）进行因式分解，如果能，请继续对多项式进行因式分解，直到每个因式都不能再分解因式为止；如果多项式的各项没有公因式，那么尝试用公式来分解因式；如果多项式的各项既没有公因式，也不能套用公式进行因式分解，那么可以尝试用分组分解法进行因式分解。

例如，分解因式

（1）2mn-6m2n+4mn2；（2）x3y-2x2y2+xy3；（3）a2-1+2ab+b2

解：（1）2mn-6m2n+4mn2=2mn·1-2mn·3m+2mn·2n=2mn（1-3m+ 2n）

（2）x3y-2x2y2+xy3=xy·x2-xy·2xy+xy·y2=xy（x2-2xy+y2）=xy（x+y）2

（3）a2-1+2ab+b2=（a2+2ab+b2）-1=（a+b）2-1=（a+b+1）（a+b-1）

2.灵活运用公式法对多项式进行因式分解的方法

（1）运用平方差公式分解因式的多项式满足的条件：①只有二项，且二项的符号一正一负；②是两个整式的平方差。例如，-x2+y2=（y+x）（y-x）；9a2-16b2=（3a+4b）（3a-4b）

（2）能用完全平方公式分解因式的多项式的特点：有三项，其中有二项是两个整式的平方且符号相同，另一项是这两个整式的积的二倍，符号可正可负。例如，-4a2+12ab-9b2=-（2a-3b）2；25m2+ 20mn+4n2=（5m+2n）2

·编辑鲁翠红