凸显课堂主体 生长学生能力——以一堂数学公开课为例

■柏黎平

凸显课堂主体生长学生能力
——以一堂数学公开课为例

■柏黎平

我校结合生本教育的先进教学思想，对数学课堂教学进行了一些改变：学生以教师课前设计的导学案为抓手，采用小组合作的自主学习结合课堂展示的方式。课堂中，教师让出了讲台，变教为学、变听为讲，课堂呈现出一种“畅所欲言”的氛围，只要你对问题有思考、有想法，就可以随时站起来（不需举手）与同学、老师进行交流。

数学导学案小组合作

数学课程标准（2011版）指出：数学教学活动要以学生为主体，要求改变课程实施过程中过于强调接受学习的现状。要倡导学生主动参与、乐于探索、勤于动手，培养学生主动搜集和处理信息的能力、获取新知识的能力、分析和解决问题的能力以及合作交流的能力。因此要求我们对传统的课堂教学方式进行相应的改进。

下面以一节《直线与圆的位置关系》公开课为例做一个简要的分析，本课的教学目标是：复习巩固基础知识并对与圆有关的临界值法求取值范围进行适当的拓展。

1.小组合作学习，生长概括归纳能力

1.1问题设置

①如图1，PA、PB分别切⊙O于点A、B，若∠P=70°，则∠C的大小为__________°。

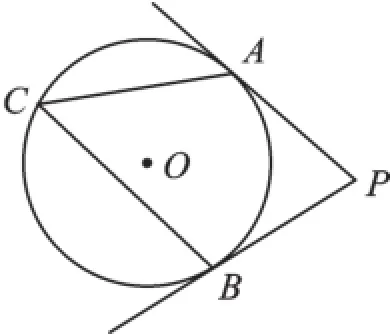
图1

②如图2，直线MN交⊙O于A、B两点，AC是直径，AD平分∠CAM交⊙O于D，过D作DE⊥MN于E，求证：DE是⊙O的切线。

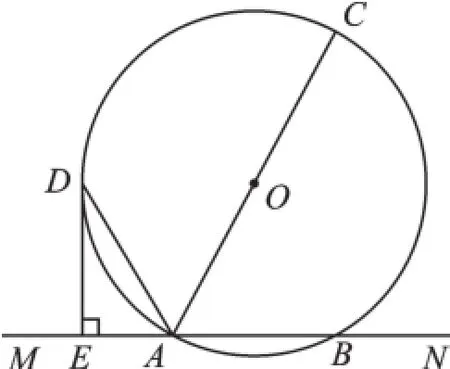
图2

两个问题由学生课前完成任务，并进行小组合作交流；在课堂上随机安排学生进行展示（困惑、晒错、心得体会等），其他小组同学可以择机与其进行交流补充。

1.2课堂实录

生1：第1题，我在解题时出错了，以为对角互补，小组讨论后知道没连半径，所以大家要注意“有切线，连半径，得垂直”。

生2：我们小组这两题没有困难，但有一个知识点忘了，什么是切割线定理，有没有同学帮忙解决一下。（是补充内容，其实与本课内容关联度不高）

生3：其实是一个补充内容……（板书图形后，很好地解决了）

生4：关于第1题，我们小组还有一个办法，连接CO，BO，可以证明∠AOB是∠ACB的一半……（讲完后发现比较麻烦），其实这个办法用的是整体思想，还是生1的方法比较好，但我的方法有时是很有用的。

师：解完上述两题后，你有什么收获吗？

生5把本课知识点直线与圆位置关系的判定与性质基本都叙述了，也不必教师重复了。

1.3分析反思

生1的错误展示具有普遍性，给其他学生一个很好的启示。倒是生2的问题有点突兀了，但是既然提出来了，我们也不能放过，估计学生中肯定有人会，因此教师并没有急于讲解，而是稍作停顿让学生思考，生3有效地解决了问题，因此我们还是要充分相信学生，放手给他们一个表现的机会，让其获得成功的体验，一定有助于提升学习数学的兴趣和信心。

这两题的学习任务以小组“合作学”为主。所谓“合作学”，即以小组为基本单位，对具体问题进行合作探究，通过组内交流研讨，自主完成对基本问题的研究。可以看到学生能通过自主的小组合作学习完成对两个小问题的掌握，只要再辅以展示错误和困惑的环节，学生应该可以完全通过。尤其是学生1、4、5在完成解题后，还对解题方法和思想进行了概括归纳，虽然不够规范，但却是其自己生长出来的语言系统，相信比教师所讲更容易让学生关注和接受，教师此时就不必多费力气，在边上坐看云涌，何乐不为呢！

2.课堂展示活动，生长观察思考能力

2.1问题设置

如图3，点A、B在⊙O上，直线AC是⊙O的切线，OC⊥OB，连接AB交OC于点D.你在读题、标图之后，可知哪些关于角或线段的关系呢？记下来，考考其他小组吧！

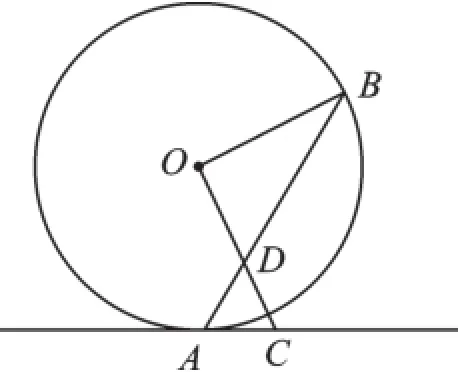
图3

本题具有开放性，学生先独立思考，再经小组讨论后进行课堂交流展示。

2.2课堂实录

生1：我们小组得到如下结论OA⊥AC、∠ODB=∠CDA、∠OAB=∠OBA。

组长刚要帮忙补充，生2已经抢先补充，但说不清，赶紧冲上黑板板演说明。

生2：我还看到了△OAC和△BOD，能否证明它们相似或全等，但是自己无法证明。

师：好想法。

生3：质疑，你是无法证明的（上台后也说不清为什么，教师想介入参与，但生3已继续）我想补充一个关于边的结论：AC=CD……

其说理过程正确，教师给予肯定，想开始解答生2的问题时，组长生4站起。

生4：我觉得点C可以运动，那么点B也将会发生运动，所以好多结论都不一定成立（多么高的境界啊），生1的结论基本都能成立，但生2相似的想法肯定就错了，可以画图试试。

2.3分析反思

“展示学”是以生为本的教育课堂教学的重要表现形式，学生通过自己的独立思考和小组合作交流后，往往都能有所得、有所悟。所以在展示过程中会呈现出多种不同的交流形式：展示所得、补充问题、帮助释疑、质疑纠错、总结心得等都是很好的生生互动、师生互动的方式，教师只需根据学生交流过程进行有针对性、有更高高度的小结，帮助学生加强对问题的深刻理解，我想应该也仅是锦上添花罢了。

在所有展示交流的过程中，生4的想法出乎我们的意料：一个静态的几何问题在其他同学的展示提醒之下，能通过自己的观察思考，提出用动态观点来解释问题的思考方式。在教师没有任何提醒的情况下，没想到我们的学生能生长出这样有价值的能力，这样有深度的理解，让我也刮目相看了！可见，我们若是真正相信学生，放手让孩子们发挥，他们生长出的能力真的很惊人啊。

3.生生交流互动，生长质疑反思能力

3.1问题设置

如图4，∠AOB=30°，OA=8，动点P在线段AO上从点A出发，以每秒1个单位的速度向O点移动，以P为圆心，2为半径作圆，设点P从A点出发运动的时间为t秒.当t在什么范围内时，⊙P与直线OB相离？

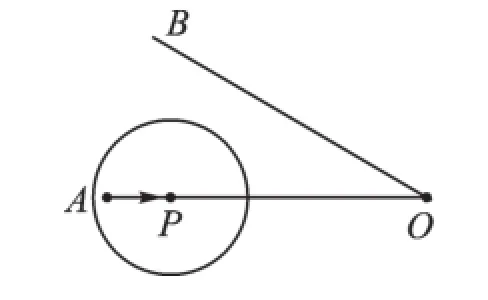
图4

学生通过解题和探究过程体会到用“临界值法”解决此类求取值范围题的优越性。学生先经独立思考，再经小组讨论后进行课堂交流，由于有点难度，若有困惑，可以寻求其他同学的帮助。

3.2课堂实录

生1：我自己算出来相切时，t=4，但组长告诉我要0≤t＜4，不知是为什么。

生2结合图形讲解，主要强调了考虑两个位置，一个出发位置，一个相切的位置，思路清晰（过程略）。生1若有所得。

生3：我觉得不需要0≤t＜4，只需要t＜4就够了，因为点P是从点A出发，t自然是大于0的，不需要多做说明。（教师还没想清楚怎么和她解释，不忙接话；生2赶紧在台上再次解释，但收效不大）

生4（马上站起来）：我问你，点P是不是从点A出发，是你还那么多废话！（有意思，要开始争论了，课堂开始热闹了，教师坚决不参与）

生3（坚持己见）：可我还是觉得只要t＜4就够了，t＜0的话，就会向左运动了，不成立的。

生5加入：点P在点A时有没有圆？是不是相离位置？是的话当然要写0。

生3若有所悟，但仍不肯放手。眼看其他同学也有“群起而攻”之势，势单力薄的生3要处于下风，教师赶紧介入，从数学答案的准确性角度解释才平息了这场“风波”。

3.3分析反思

本题虽小有难度，但大部分学生都应该没问题，所以教师原本的重点其实在下面的变式上，没曾想半路杀出个程咬金（学生3），由于学生都是具有各自鲜明特征的生命，其学习的最近发展区和认知能力有差异，所以其思考方式会有所不同，出现这样或那样的问题并不奇怪。在这样的课堂中，教师让出讲台，把话语权交还给学生后，各种各样的质疑和思考都会生长出来，若都能有效解决，学生的能力肯定有所提高。我们的课堂允许学生张扬个性、充满困惑的学习，关键是发现问题后如何引导学生进行正确的思维。再看生3，这个本不是问题的问题，恰是其在自主思考后生长出来的，敢于质疑反思，值得欣赏。回顾其课堂上舌战群雄的架势，是否让我们想起了布鲁诺、哥白尼那种坚持真理永不放弃的精神？

以上仅用三个课堂片段简单解释了我们在课堂教学方式改进上的做法与思考，应该还有很多不足等待笔者思考和探索实践加以解决。

在日常教学中，我们经常会对学生的学习天性和潜能估计不足，觉得凡事都需经教师传授才能获取知识，殊不知学生与生俱来的学习天性是惊人的。只要我们在数学课堂教学中能凸显学生学习的主体性原则，敢于放手让学生自主探索获取知识，也完全可以让孩子的学习能力自由生长。

（作者为江苏省太仓市双凤中学教师）