飞蛾火焰优化算法在承压含水层参数反演中的应用

崔东文



飞蛾火焰优化算法在承压含水层参数反演中的应用

崔东文

（云南省文山州水务局，云南文山663000）

通过10个典型低维函数对一种新型群体智能仿生算法——飞蛾火焰优化（MFO）算法进行仿真验证，并与粒子群优化（PSO）算法的寻优结果进行对比。以无界井流问题及直线隔水边界附近井流问题的解析解为基础，将MFO算法应用于分析抽水试验数据，进行反演承压含水层参数，并以2个实例对MFO算法进行验证。结果表明：MFO算法在低维函数极值寻优问题上具有较好的收敛精度和全局寻优能力，寻优精度较PSO算法提高了7个数量级以上。MFO算法对2个实例的反演精度较文献改进SA算法等提高了56．5%以上，具有较好的稳健性能、收敛速度和全局寻优能力。利用MFO算法对承压含水层参数进行反演，可获得比相关文献更高的反演精度，不但为精确估计承压含水层参数提供了有效方法，而且拓展了MFO算法在地下水模型参数反演中的应用，具有良好的应用价值和前景。

飞蛾火焰优化算法；粒子群优化算法；仿真验证；含水层参数；参数反演

doi：10．11988/ckyyb．20150694

1　研究背景

含水层参数的确定，对于建立地下水流运动数学模型、科学评价和管理地下水资源具有重要意义。目前确定含水层参数的主要方法是利用抽水试验数据，通过标准曲线配线法［1］、Jacob图解法［1］进行确定，虽然计算过程简便，但存在主观随意性强、精度低和对野外观测条件苛刻等问题。近年来，随着智能优化算法的不断改进和人工智能技术逐渐走向成熟，各种智能优化算法被尝试用于地下水模型参数的反演，取得了比传统曲线配线法、Jacob图解法更好的反演效果，如遗传算法［2-3］（genetic algorithm，GA）、混沌优化算法［4］（chaos optimization algorithm，COA）、模拟退火算法［5］（simulated annealing，SA）及其改进算法［6-7］、粒子群优化算法［8］（particle swarm optimization，PSO）及其改进算法［9］、微分进化算法［10］（differential evolution，DE）等。在智能优化算法领域，“没有免费午餐”定理在逻辑上证明了没有一种优化算法能求解所有的优化问题。因此，近年来智能优化算法间的融合与改进以及新型仿生算法的不断提出正呈现蓬勃发展之势。飞蛾火焰优化（moth-flame optimization，MFO）算法是文献［11］于2015年提出的一种新型仿生群体智能算法，该算法灵感源于自然界飞蛾横向定位导航机制，并基于飞蛾-火焰（灯光）螺旋飞行数学模型而发展起来的一种全局优化算法，用以解决不同领域的优化问题，具有调节参数少、收敛精度高和鲁棒性能好等特点。

将智能优化算法用于地下水模型参数反演过程中，由于模型参数反演解的不唯一性，要想获得理想的反演效果，要求智能优化算法具有较好的全局寻优能力和收敛精度。本文以无界井流问题及直线隔水边界附近井流问题的解析解为基础，利用MFO算法对承压含水层参数进行反演，主要做法如下：①由于承压含水层参数反演为低维优化问题，因此选取10个典型低维测试函数对MFO算法进行仿真验证，并与PSO算法的寻优结果进行比较；②以文献［2］中的2个实例对MFO算法进行验证，并与文献［2］中改进SA算法等方法的反演结果进行比较，旨在拓展MFO算法在相关地下水模型参数反演中的应用。

2　反演模型

2．1MFO算法数学描述

MFO算法灵感源于自然界飞蛾横向定位导航机制，并通过飞蛾-火焰螺旋飞行数学模型更新飞蛾-火焰位置，并最终收敛于火焰（灯光）位置的新型群体智能仿生算法。MFO算法选择螺旋函数作为飞蛾空间位置的更新算子，并在优化过程中遵行以下准则：①螺旋的初始点从飞蛾初始化空间位置开始，最后一点为火焰的最佳空间位置；②螺旋的波动范围不超出搜索空间；③在火焰周围，飞蛾能够随t（t为［-1，1］之间的随机数）的变化而收敛到任何点，t越小，离火焰的距离越近；④当飞蛾靠近火焰时，火焰两侧的位置更新频率增加。

MFO算法数学模型描述如下［11］：

设待优化问题的候选解及问题变量为飞蛾所处空间位置，利用式（1）矩阵表示飞蛾种群规模为n、优化问题维度为d的飞蛾所处的空间位置；利用式（2）矩阵存储飞蛾个体适应度值。

MFO算法中另一关键部分是火焰。其矩阵类似于飞蛾矩阵，表示为

并利用式（4）矩阵存储火焰适应度值，即

式中：n为飞蛾种群规模；d为优化问题维度。

在这里，飞蛾和火焰均为候选解，其区别在于二者在进化过程中位置的更新方式。飞蛾是在搜索空间附近移动的搜索动因，而火焰是当前迭代所获得的最佳位置。即通过火焰位置不断更新直至获得最佳位置（候选解）。因此，MFO算法可定义为式中：I为随机生成的飞蛾种群规模和相应的适应值函数值；P为飞蛾在搜索空间移动的函数，其为M矩阵和位置更新返回值；K为终止条件是否满足的判别函数。

用数学模型描述飞蛾-火焰位置更新如下：

式中：Mi表示第i只飞蛾位置；Fj表示第j个火焰；S为螺旋函数。

定义用于模拟飞蛾螺旋飞行路径的MFO算法表达式如下：

式中：Di为第j个火焰到第i只飞蛾的距离，表示为为螺旋形状常数；t为［-1，1］之间的随机数。

式中：l为当前迭代次数；N为最大火焰数量；T为最大迭代次数。

从式（7）可以看出，飞蛾的下一个位置被定义为一个火焰；参数t定义了飞蛾的下一个位置应该接近的火焰（t=-1表示最接近火焰位置，而t=1表示离火焰位置最远）。因此，假定超椭圆为所有方向上旋转的火焰，且飞蛾的下一个位置在该空间内。螺旋位置更新算子决定了飞蛾如何在火焰周围进行位置更新；螺旋函数方程允许不一定在该空间内的飞蛾“围绕”火焰飞翔，有效保证了MFO算法探索和开发空间的能力。

2．2适应度函数

［2］，对于在平面上无限展布均质各向同性承压含水层中的完整井作抽水试验，含水层满足泰斯（Theis）模型的假定条件时，观测井中的水位降深用Theis模型的解析解来表示。其解析表达式为

为保证MFO算法获得较快的收敛速度，提出自适应火焰数量更新机制，即利用在迭代过程中自适应地减少火焰的数目。其公式为

式中：s∧为水位降深；Q为定流量抽水量；Z为含水层导水系数；W（u）为泰斯井函数；r为观测孔距抽水井的距离；S为含水层储水系数；x为抽水时间；u无因次。

利用无界含水层中的叠加原理，便可得到直线隔水边界附近井流问题的解析解，即

式中ri为第i个观测孔距抽水井的距离。

本文采用文献［2］中的方法近似计算泰斯井函数W（u）值。并构建目标适应度函数为

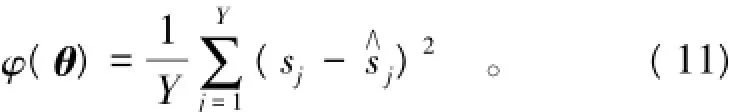
式中：s为第j时刻的实测水位降深（m）；∧s为利用

式（9）或式（10）计算的第j时刻水位降深（m）；j为抽水序列号，j=1，2，…，Y；θ为待估参数向量，对于实例1，θ=（Z，S）；对于实例2，θ=（Z，S，r2）。

2．3MFO算法参数反演实现步骤

利用MFO算法进行参数反演的基本思想是：在参数寻优范围内搜索一组θ=（Z，S）或θ=（Z，S，r2），使得式（11）达到最小。MFO算法参数反演实现步骤归纳如下所述。

Step 1：确定待优化参数θ的维度、搜寻范围和算法迭代终止条件；利用抽水试验数据率定最佳参数θ，以期获得模拟效果更佳的水位降深模型。

Step 2：确定MFO算法的适应度函数。适应度函数是描述种群个体优劣程度的主要指标，本文选用式（11）为目标适应度函数。

Step 3：初始化算法参数。设置最大迭代次数T、飞蛾种群规模n、搜索空间维数d以及最大火焰数量N，令当前迭代次数l=0。

Step 4：计算飞蛾个体适应度函数值，并找到当前最好飞蛾个体位置并将其保存为火焰适应度值矩阵。判断算法迭代终止条件是否满足，若满足则转至Step 8，否则执行Step 5。

近日，湖北澳特尔化工有限公司与全国农技推广中心，在山东省平度市大泽山镇南昌村，召开澳特尔玫瑰香葡萄营养套餐肥高产高效示范观摩会，吸引当地150多名种植大户到场观摩，青岛市和平度市两级土肥站负责人都到场参会并为该肥叫好。

Step 5：迭代过程。利用式（8）更新火焰数量；计算火焰与飞蛾间的距离，并利用式（7）更新飞蛾-火焰位置。

Step 6：计算飞蛾个体适应度函数值，利用式（2）、式（4）分别保存飞蛾及火焰空间位置。

Step 7：找到当前最好飞蛾个体空间位置。如果当前位置优于前次保留位置，则保留当前火焰位置为最佳位置。判断算法迭代终止条件是否满足，若满足则转至Step 8，否则令l=l+1，并执行Step 5—Step 7。

Step 8：输出最优个体值和全局极值，即火焰最终所处的空间位置及所对应的适应度值，算法结束。

3　算法验证

文献［11］证明了MFO算法对于高维测试函数的寻优效果整体上要优于粒子群优化算法（PSO）、引力搜索算法（GSA）和蝙蝠算法（BA）。本文针对承压含水层参数反演的低维优化问题，选取10个典型低维函数（见表1）作为验证对象，进行仿真验证，求测试函数的极值，并与PSO算法寻优结果进行比较，比较结果见表2。

MFO和PSO算法具体参数设置如下：MFO算法，飞蛾种群规模n及最大火焰数量N均为200，最大迭代次数T=1 000；PSO算法，最大迭代次数T= 1 000，种群规模n=200，=0．729，局部学习因子、全局学习因子c1=c2=1．494 45，个体速度限制为［-0．5，0．5］。每个测试函数均独立运行20次，分别求出最优值、最劣值、平均值、标准差和计算成功率5个方面对3种算法进行评估，当满足式（12）时，即认为当前寻优计算成功。

表1　基准函数Table 1　Reference functions

表2　函数优化对比结果Table 2　Comparison of the results of function optimization

式中：F为函数的理想最优值；F*为每次寻优计算所得最优函数值。

从表2可以看出，除 Easom，Six Hump Camel Back函数MFO算法与PSO算法寻优结果相同外，MFO算法对其余8个函数的寻优效果要远远优于PSO算法。其中，MFO算法对Booth函数、Bohachevsky1函数、Schaffer函数、Bohachevsky3函数和Bridge函数的寻优获得了理论最优值；对于Rosenbrock函数、Matyas函数、Eggcrate函数的寻优也获得了较好的寻优效果，其获得的最优值、最劣值、平均值和标准差均比PSO算法的优化结果提高了7个数量级以上，寻优成功率均达到100%。表明MFO算法在低维函数极值寻优问题上具有较好的收敛精度和全局寻优能力，能有效避免算法陷入局部最优。

4　实例应用

本文利用MFO算法对文献［2］中的2个承压含水层参数反演实例为例进行验证，并与文献［2］中的改进SA算法等方法的反演结果进行比较。

4．1实例1

有一承压含水层做定流量抽水试验，假定该含水层的水文地质条件满足Theis井流模型的假定条件。已知观测孔距抽水井的距离r=100 m，主井做定流量抽水，抽水量Q=162．9 m3/min，抽水过程中观测井不同时刻的降深观测值见表3。利用MFO算法反演参数（Z，S）。

表3　实例1及实例2抽水试验数据Table 3　Result of pumping test in case 1 and case 2

MFO算法参数设置：飞蛾种群规模n及最大火焰数量N均为200，最大迭代次数M=100，参数Z，S的搜索空间分别为（3，300）和（0．006，0．6）。

利用MFO算法对该实例参数Z，S进行反演，其结果与文献［2］中的改进SA算法等方法的反演结果进行比较，见表4；并给出MFO算法连续5次进化过程图，见图1。

表4　实例1参数反演结果及比较Table 4　Comparison of parameter inversion result in case 1

图1　实例1连续5次进化过程Fig．1　Evolution process for five consecutive times in case 1

4．2实例2

直线隔水边界附近有一承压含水层做定流量抽水试验，该含水层其它水文地质条件与Theis井流中的水文地质条件相同。已知观测孔距抽水井r1= 30．48 m，主井做定流量抽水，抽水量 Q=4．581 m3/min。抽水过程中不同时刻的降深观测值见表3。利用MFO算法反演参数）。

MFO算法参数设置：飞蛾种群规模n及最大火焰数量N均为200，最大迭代次数M=100，参数Z，S的搜索空间分别为（0．3，300），（0．00，1．00），（10，1 000）。

利用MFO算法对该实例参数Z，S，r2进行反演，其结果与文献［2］中的改进SA算法的反演结果进行比较，见表5；并给出MFO算法连续5次进化过程图，见图2。

表5　实例2参数反演结果及比较Table 5　Comparison of parameter inversion result in case 2

图2　实例2连续5次进化过程Fig．2　Evolution process for five consecutive times in case 2

从表4、表5和图1、图2可以看出：

（1）对于实例1，MFO算法的反演精度较Theis方法、Coopor-Jacob方法和改进SA算法分别提高了92．7%，63．5%，56．3%；对于实例2，MFO算法的反演精度较改进SA算法提高了99．0%，表明MFO算法具有较好的收敛精度和全局寻优能力。

（2）从2个实例来看，MFO算法连续5次运行的寻优结果均一致，参数反演结果除实例2第3次反演略微变动外，其余各次的反演结果均一致；从图1和图2来看，MFO算法连续5次运行，其分别进化到第30代和第50代左右时就分别收敛到相对全局最优解4．347 2×10-5m2及3．982 9×10-5m2，表明MFO算法具有较好的稳健性能和较快的收敛速度。

5结论

本文基于抽水试验数据，利用一种新型群体智能仿生算法——MFO算法反演承压含水层参数，通过10个典型低维测试函数对MFO算法进行仿真验证，并以文献［2］中2个实例为验证对象，结果表明：

（1）MFO算法在低维函数极值寻优问题上具有较好的收敛精度和全局寻优能力，寻优精度较PSO算法提高了7个数量级以上，能有效避免算法陷入局部最优。

（2）利用MFO算法反演承压含水层参数，不但可有效提高了承压含水层参数的反演精度，而且为地下水模型参数反演提供了一种全新的途径和方法。

（3）从2个实例的反演效果来看，MFO算法的反演精度较改进SA算法等提高了56%以上，表明MFO算法能有效解决传统方法及改进SA算法等存在的早熟收敛和陷入局部极值问题，进一步提高了地下水模型参数的反演精度，具有较好的应用价值和前景。

［1］ 陈崇希，林敏．地下水动力学［M］．武汉：中国地质大学出版社，1999．

［2］张娟娟．智能优化算法在含水层参数反演中的应用［D］．西安：长安大学，2006．

［3］姚磊华，李竟生．综合改进的遗传算法反演三维地下水流模型参数［J］．岩石力学与工程学报，2004，23（4）：625-630．

［4］郭建青，李彦，王洪胜，等．确定含水层参数的混沌序列优化算法［J］．中国农村水利水电，2006（12）：26-29．

［5］李守臣，上官子昌，刘迎曦，等．地下水渗流模型参数识别的模拟退火算法［J］．岩石力学与工程学报，2005，24（1）：5031-5036．

［6］ 张娟娟，郭建青，韩淑敏，等．基于改进模拟退火算法反演水文地质参数［J］．中国农村水利电，2005（9）：8-11．

［7］韩一龙，单永明．运用模拟退火遗传算法估计地下水反演参数［J］．计算机工程与应用，2012，48（12）：224-228．

［8］张鹄志，郭建青．粒子群优化算法在确定越流含水层参数中的应用［J］．水利水电科技进展，2011，31（3）：13-16．

［9］袁帆，刘元会，郭建青，等．利用单纯形-粒子群混合算法确定越流含水层参数［J］．南水北调与水利科技，2015，13（4）：729-732，755．

［10］郝竹林，冯民权，闵涛，等．地下水渗流参数反演的微分进化算法［J］．自然灾害学报，2015，（1）：55-60．

［11］MIRJALILI S．Moth-Flame Optimization Algorithm：A Novel Nature-inspired HeuristicParadigm［J］．Knowledge-Based Systems，2015，89：228-249．

（编辑：王慰）

Application of Moth-flame Optimization Algorithm in Parameter Inversion of Confined Aquifer

C
UI Dong-wen
（Water Authority of Wenshan Autonomous Prefecture in Yunnan Province，Wenshan663000，China）

Through 10 typical low dimensional functions，we validate a new kind of swarm intelligent bionic algorithm by simulation，namely moth-flame optimization（MFO）algorithm．We compare the optimization results between MFO algorithm and particle swarm optimization（PSO）algorithm．On the basis of analytical solution of well flow problem without boundary and water flow problem near straight boundary for water insulation，we apply MFO algorithm to analyzing pumping test data and carry out parameter inversion of confined aquifer．Two examples are used to verify MFO algorithm．Results show that，1）MFO algorithm has advantages such as high convergence accuracy and good global optimization ability in the optimization problem for low dimensional function extremum，which is superior to PSO algorithm，and optimization accuracy of MFO algorithm is higher than that of PSO algorithm by 7 orders of magnitude；2）MFO algorithm has good robustness，fast convergence speed and global optimization ability，exceeding improved SA algorithm by 56．5%in inversion accuracy for the 2 examples；3）by using MFO algorithm，we can have an effective method to estimate the parameters of confined aquifer，and also effectively conduct parameter inversion for underground water model．Finally，in comparison with methods in relevant literatures，MFO algorithm has better inversion accuracy and good application value．

moth-flame optimization algorithm；particle swarm optimization algorithm；simulation verification；aquifer parameter；parameter inversion

P641．8

A

1001-5485（2016）07-0028-06

2015-08-21；

2015-10-26

崔东文（1978-），男，云南玉溪人，高级工程师，主要从事水资源水环境研究及水资源保护等工作，（电话）0876-2122879（电子信箱）cdwgr@163．com。