长江沙市段断面面积对水沙变异的滞后响应研究
章运超,李凌云,1b,范北林,1b,郑 珊
长江沙市段断面面积对水沙变异的滞后响应研究
章运超1a,李凌云1a,1b,范北林1a,1b,郑珊2
(1.长江科学院a.河流研究所;b.水利部江湖治理与防洪重点实验室,武汉430010;2.武汉大学水利水电学院,武汉430072)
通过长江中游沙市站的实测水沙、断面资料的分析表明,沙市站河槽形态的调整对水沙变异存在一定滞后性。为了研究沙市河段河床演变的滞后响应规律,从3个方面对适用于黄河流域的河床演变滞后响应模型进行改进:①以沙市站多年平均枯水位下的断面面积作为滞后响应模型的特征变量;②引入“年组合流量”概念;③在模型迭代公式中使用分段函数,从而得到适用于沙市河段的河床演变滞后响应模型。利用模型迭代公式进行计算,结果表明改进后的河床演变滞后响应模型计算精度R2处于0.7~0.8之间,可以很好地描述沙市站河槽形态的调整规律。
冲积河流;河床演变;水沙变异;滞后响应;断面面积;长江沙市站
doi:10.11988/ckyyb.20150336
1 研究背景
大量的观测和研究表明,天然冲积河流均衡河道的形成是一种自我调整的过程,河床演变是由水流与河床相互作用中的输沙不平衡所引起的[1]。上游来水来沙的变化影响着河槽形态的调整,但是河槽形态的调整变化一般滞后于水沙条件的变化,存在一定的滞后响应现象。
牛占等[2]建立了黄河流域1976—1996年间各水文测站断面的当年汛前主槽断面面积与花园口站前5 a内流量>3 000 m3/s的平均天数及花园口站前5 a的年平均来水量具有较好的相关关系。梁志勇等[3]基于“记忆”效应,建立了黄河下游3个河段的断面河槽形态指标(平滩面积、河宽、水深、河相系数)与前期水沙因子的关系,认为河槽形态指标与前期3~5 a水沙因子之间的相关性最好。冯普林等[4]将此方法扩展到黄河流域大量统测断面,认为断面河槽形态AN是前期年份流量Q及含沙量S的连续函数:A=aQbSc(a,b,c为指数)。
N几何均值几何均值林秀芝等[5]分析了渭河下游华县站平滩流量与多年平均来水量滑动平均值的关系,发现平滩流量与0.7倍当年来水量和0.3倍上年来水量的加权平均水量相关最好;同时发现平滩流量与0.8倍当年最大3 d流量平均值和0.2倍上一年平滩流量加权组合值的相关性较好。吴保生等[6]探讨了黄河下游平滩流量对水沙条件变化的滞后响应规律,发现采用滑动平均汛期流量和滑动平均汛期来沙系数基本上能够反映前期水沙条件对平滩流量的影响效果,当滑动平均年数为4~5 a时相关性最好,将此方法运用到黄河下游高村站时[7],提出了高村站平滩面积的计算公式。近期Xia等[8]研究了2002—2012年间荆江流域4个河段断面资料,引入“河流侵蚀强度”Ff作为河岸崩塌的主要影响因子,认为平滩河宽可以表示为前期n年汛期平均“河流侵蚀强度”的指数函数,验证结果显示当n=5 a时的相关性最好。
吴保生[9]基于冲积河流自动调整的基本原理,提出了冲积河流河床演变的滞后响应模型,阐明了前期水沙条件对河床演变滞后影响的物理本质。图1所示为具体的响应过程。
根据图1所示滞后响应过程,河槽形态的特征变量从一个原有状态调整至新平衡状态的过程可用一阶常微分方程描述,即
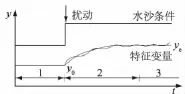
图1 冲积河流系统受外部扰动后的滞后响应模式Fig.1 Delayed response patterns for alluvial river systems in response to external disturbance

图1和式(1)中:y为河床演变特征变量;ye为特征变量y的平衡值,一般与流量及含沙量相关;y0为特征变量y的初始状态;t为时间;β为系数,β可以随时间变化,为了求解方便,一般取为常数。对式(1)进行积分求解,通过多步递推得到n个迭代时段内河床调整结果的递推模式为式中:n表示滞后响应迭代时段数;i表示各个时段的编号;Δt表示各个时段的长度;yn表示经过前期n个时段累计作用后的特征变量值;yei为第i年的特征变量平衡值。

总结起来,以往的研究多是建立各类河槽形态特征变量与水沙因子当年值及前期值之间的相关关系,缺乏实质的理论根据。吴保生等提出的河床演变滞后响应模型在黄河流域取得了很好的效果,但直接运用到其他流域效果不明显,本文拟在该模型的基础之上,推导出适用于长江中游沙市河段的河床演变滞后响应模型。
i=1
2 沙市站水沙变化分析
沙市河段位于长江中游的荆江河段,上起陈家湾,下至玉和坪,全长22 km。沙市水文站是该河段水沙特征的代表站,控制流域面积103万km2,是长江中游重要的防洪控制站。
2.1水沙年际变化
通过分析沙市站历年(1956—2011年)实测水沙数据可知,沙市站多年平均径流量3 896亿m3,多年平均输沙量3.74亿t。沙市站最大年径流量为1998年的4 751亿m3,最大年输沙量为1968年的6.56亿t;年径流量最小值为2006年的2 795亿m3,年输沙量最小值为2011年的0.18亿t。图2中的(a)和(b)分别显示了1956—2011年间沙市站年径流量和输沙量的变化过程。
从图2中可看出葛洲坝工程蓄水前(1956—1980年)沙市站年径流量和输沙量总体上围绕多年平均值上下波动,表现出“水多沙多,水少沙少”的变化规律。1981年葛洲坝工程建成蓄水后,年径流量继续保持稳定波动,而年输沙量开始呈现小幅度减少。2003年三峡工程蓄水后,库区拦蓄了大量泥沙,“清水下泄”造成了年输沙量的急剧下降。本文依据葛洲坝工程蓄水时间(1981年)和三峡工程蓄水时间(2003年)划分出3个计算时段,表1列出了3个时段内沙市站的多年平均径流量和多年平均输沙量,以及各时段汛期径流量和汛期输沙量占全年的比例。可以看出沙市站年径流量和年输沙量总体上呈下降趋势。1980—2002年间平均径流量和年平均输沙量分别为4 037亿m3和4.1亿t,与1956—1980年相比,年径流量有所增加但年输沙量减少了10.7%;2003—2011年间平均径流量和平均输沙量分别为3 706亿m3和0.7亿t,与1980—2002年相比,年径流量和年输沙量分别减少了8.2%和82.7%。

图2 沙市站年径流量和输沙量变化过程Fig.2 Variations of annual runoff and sediment discharge at Shashi station

表1 沙市站不同时段多年平均径流量及输沙量Table 1 Annual mean runoff and sediment discharge in different periods at Shashi station
2.2水沙年内变化
由表1可以看出,1956—1980年汛期(5—10月份)径流量占全年径流量的比例为77%,汛期输沙量占全年输沙量的比例为93.1%;1981—2002年汛期径流量和汛期输沙量占全年的比例分别为76.4% 和95.1%;2003—2011年汛期径流量和汛期输沙量占全年的比例分别为72.2%和93.2%。
这与汛期时长占全年总时长的比例(50%)是不一致的,由此可知沙市站水沙年内分配的不均匀,具体的差异可以从图3看出。
沙市站历年来各月径流量和输沙量均以7月份最大,2月份最小,径流量和输沙量的年内变化呈正相关。葛洲坝工程蓄水后,各月平均径流量略微增加,但输沙量有小幅度减少。三峡工程蓄水后,由于出库流量的调节,汛期径流量相应减少,2003—
2011年间 7月平均径流量减少最多,比 1981—2002年间7月份平均径流量减少了18%;枯水期(11月份—次年4月份)径流量同比增大,2003—2011年3月份平均径流量增加最多,比1981—2002 年3月份平均径流量增加了22%。由于大量泥沙被拦蓄在库区,输沙量在汛期和枯期均有减少,2003—2011年 7月份平均输沙量减少最多,比 1981—2002年7月份平均输沙量减少了84%。

图3 沙市站不同时段月平均径流量和月平均输沙量Fig.3 Monthly mean runoff and monthly mean sediment discharge in different periods at Shashi station

图4 沙市站断面面积A与不同水沙因子滑动平均年值间的相关关系Fig.4 Variation legend of correlation coefficient between cross section area A and moving average water sediment factors at Shashi station
2.3断面面积对水沙条件变化的响应
沙市河段地处长江中游,属于典型的冲积性河流。上游葛洲坝和三峡水利枢纽的建成改变了沙市段的来水来沙条件,进而触发沙市河段河槽形态作出相应的调整。本文选取沙市站多年平均枯水位下的断面面积A(下文简称“断面面积A”)作为河床演变的特征变量,分别计算汛期平均来沙系数ξf及年组合流量Q组合的前期年份滑动平均值与断面面积A之间的相关关系,其中来沙系数ξ为含沙量S与流量Q的
比值,本文选取的ξf为日均来沙系数的汛期平均值,Q组合的计算过程见式(5)—式(7),计算结果见图4。
由图4可知,断面面积A与当年水沙条件的相关性都很低,断面面积A与当年汛期平均来沙系数、当年年组合流量之间的相关性系数R2分别为0.21,0.05。但随着滑动平均年数n的增加,相关系数不断提高,断面面积A分别与汛期平均来沙系数前期5 a滑动平均值、年组合流量前期2 a滑动平均值的相关性最高。随着n的进一步增大,相关系数开始下降,这表明沙市站断面面积A的调整不仅受当年水沙条件影响,更与前期水沙条件有关,且前期水沙条件对断面面积A的影响存在一定滞后性,这点将在下文详叙。
3 滞后响应模型的改进及应用
3.1原滞后响应模型
李凌云等[10-11]基于一维河床冲淤变形方程和不平衡输沙方程,推导了冲积河流滞后响应模型的基础方程,从几个方面对滞后响应模型的结构进行了改进,并在黄河流域取得了很好的试验效果。经过调整,公式(2)改写为

将模型运用到黄河下游时,引入了洪峰流量(年内最大日均流量)以体现其对河槽形态的影响,Qei计算公式为

式(3)、式(4)中:Qbn为经n年累积后的平滩流量值、Qei为第i年末平滩流量平衡值、Qmi为第i年最大日均流量、Qfi为第i年汛期平均流量(m3/s);ξfi为第i年的汛期平均来沙系数(kg·s·m-6);K为系数;a,b,c为指数。

图5 冲积性河流典型河道横断面Fig.5 Schematic diagram of typical cross section inalluvial river
3.2滞后响应模型的改进
吴保生[12]和李凌云等[10,13]对冲积河流滞后响应模型的研究取得了很好的试验效果,但计算成果均局限在黄河流域。廖治棋[14]在荆江河段运用滞后响应模型进行试验研究,模型的计算精度R2还需提高。本文从以下3个方面对滞后响应模型进行改进。
3.2.1选取多年平均枯水位下的断面面积作为模型特征变量
冲积性河流的河道横断面形态一般分为主槽、滩地2部分,如图5所示,其中z1表示河道流量较小时的水位线;z2表示与河漫滩表面相平时的水位线,称平滩水位;z3表示漫滩后的水位线。其中水位线z2以下的主槽断面面积称为平滩面积[15]。一般研究中多以平滩面积来反映河道横断面的冲淤变化。
尽管平滩面积和平滩水位的物理概念很清晰,但长江中游多处河段的滩槽过渡不明显甚至没有河漫滩,根据图6所示的沙市站1991—2011年间的断面变化图可看出,由于两岸堤防的束缚,无法根据物理概念确定沙市站的平滩面积。

图6 沙市站1991—2011年间汛期断面变化Fig.6 Change of cross section in flood season at Shashi station between 1991 and 2011
本文搜集了沙市站1991—2011年历年枯水期的平均水位,求得多年平均枯水位为32.4 m。再依据沙市站实测断面资料计算出多年平均枯水位下的断面面积A,并将其作为滞后响应模型中的特征变量,通过断面面积A的变化来反映河槽形态的变化。
3.2.2引入年组合流量概念
黄河流域“水少沙多”,且来水来沙主要集中于汛期,式(2)、式(3)中水沙影响因子主要是汛期平均来沙系数ξf和汛期平均流量Qf。长江的来沙量较黄河少,但来水量较黄河更多,非汛期来水量对河床冲淤调整的过程不容忽略,为此引入年组合流量:

式中:Qf和Qnf分别为汛期和非汛期平均流量(m3/s);Wf,Wnf,W年分别为汛期总来水量、非汛期总来水量、年总来水量(m3);A,B为系数。式(4)改动为

式中:Aei表示第i时刻断面面积A的平衡值(m2);Q组合i表示第i年的年组合流量(m3/s)。
3.2.3采用分段函数进行计算
长江干流中有葛洲坝和三峡2大水利枢纽,大坝的修建势必改变了下游的来水来沙条件,改变下游河道的冲淤情况,影响河道断面面积。本文以葛洲坝工程蓄水时间(1981年)和三峡工程蓄水时间(2003年)为时间节点,结合模型迭代式(3)和式(8),得到沙市站断面面积A与水沙因子之间的滞后响应模型迭代公式。


式中:An为经过前期n年累计作用后的断面面积A;a1,b1,c1,β1,a2,b2,c2,β2均为系数,根据实测资料率定;Δt取1 a。
3.3滞后响应模型的计算结果
首先计算出沙市站1991—2011年多年平均枯水位32.4 m水位下的断面面积A,并将其作为滞后响应模型中的特征变量。而后依次增加前期影响年数n的取值,根据沙市站水沙和断面资料,分别拟合出模型迭代式(9)、式(10)中的系数和参数。最后得到n 为0~10 a时的模型计算值,对比计算值与断面面积A的实测值,得到不同影响年数n的模型计算精度指标R2值。由图7显示的计算结果知,改进后的滞后响应模型在沙市站取得不错的效果:2003—2011年间,沙市站断面面积A与前期5 a(n=4 a)的水沙条件相关性最高,对比模型计算值与实测值得到的相关性系数R2为0.79;1991—2002年间沙市站断面面积A与前期7 a(n=6 a)的水沙条件相关性最高,对比模型计算值与实测值得到的相关性系数R2为0.70。为加强对比本文还对1991—2011年断面数据进行了直接计算,结果显示模型计算值与实测值间相关性较差,n= 5 a时相关性系数R2取最大值0.43,远小于0.79和0.70。表2为分段函数的系数值。
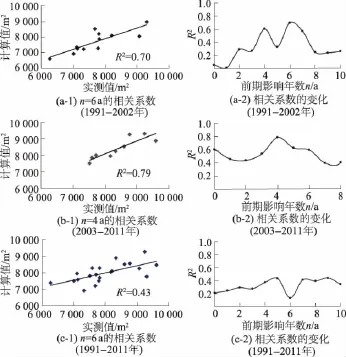
图7 沙市站模型断面面积A计算值与实测值间相关关系Fig.7 Correlation of the calculation values of cross section A with the measured values at Shashi station

表2 沙市站滞后响应模型迭代公式系数值Table 2 Coefficients of iterative formula in the delayed response model
4 结论与分析
(1)沙市河段地处长江中游,属于典型冲积性河道,其水量丰富但水流含沙量较小。葛洲坝和三峡工程修建后,一方面“清水下泄”造成了沙市河段输沙量的大幅减少,引起河床剧烈冲刷;另一方面由于水库的拦蓄作用,沙市河段来水量和来沙量在年内分配趋于稳定。水利枢纽的兴建改变了下游来水来沙条件,进而改变河槽形态。
(2)由于长江流域与黄河流域的巨大差别,使得适用于黄河流域的河床演变滞后响应模型在长江流域的直接使用的效果并不明显,本文在黄河流域河床演变滞后响应模型的基础上,从引入“年组合流量”概念;以沙市站多年平均枯水位下的断面面积作为模型的特征变量;在模型迭代公式中使用分段函数这3个方面做出改进,推求出适用于长江中游沙市河段的河床演变滞后响应模型迭代公式。
(3)本文对长江中游的河床演变滞后响应模型的计算理论和计算方法做出了探索,将改进后的河床演变滞后响应模型应用到沙市站时,取得了很好的计算精度。对比模型计算值与实测值之间的相关性,相关性系数R2在0.7~0.8之间,相关性很高,后期还需使用更多的站点对长江流域进行整体的、全面的研究。参考文献:
[1] 钱宁,张仁,周志德.河床演变学[M].北京:科学出版社,1989.
[2] 牛占,田水利,王丙轩,等.1977—1996年黄河下游水文断面反映的河床演变[J].泥沙研究,2000,(3):21-29.
[3] 梁志勇,杨丽丰,冯普.黄河下游平滩河槽形态与水沙搭配之关系[J].水力发电学报,2005,24(6):68-71.
[4] 冯普林,梁志勇,黄金池.黄河下游河槽形态演变与水沙关系研究[J].泥沙研究,2005,(2):66-73.
[5] 林秀芝,田勇,伊晓燕,等.渭河下游平滩流量变化对来水来沙的响应[J].泥沙研究,2005,(5):1-4.
[6] 吴保生,夏军强,张原锋.黄河下游平滩流量对来水来沙变化的响应[J].水利学报,2007,38(7):886-892.
[7] 吴保生,张原锋,夏军强.黄河下游高村站平滩面积变化分析[J].泥沙研究,2008,(2):34-40.
[8]XIA Jun-qiang,ZONG Quan-li.Prediction of Recent Bank Retreat Processes at Typical Sections in the Jingjiang Reach[J].Science China,2014,57(8):1482-1489.
[9] 吴保生.冲积河流河床演变的滞后响应模型-I模型建立[J].泥沙研究,2008,(6):1-7.
[10]李凌云.黄河平滩流量的计算方法及应用研究[D].北京:清华大学,2010.
[11]李凌云,吴保生,侯素珍.滞后响应模型在黄河内蒙古河段的应用[J].水力发电学报,2011,30(1):70-77.
[12]吴保生.冲积河流河床演变的滞后响应模型-Ⅰ模型应用[J].泥沙研究,2008,(6):30-37.
[13]李凌云,吴保生.渭河下游平滩流量的预测[J].清华大学学报(自然科学版),2010,50(6):852-856.
[14]廖治棋.荆江河段平滩面积对水沙条件变化的滞后响应研究[D].武汉:长江科学院,2014.
[15]谢鉴衡.河床演变及整治[M].北京:水利水电出版社,1990.
(编辑:王慰)
Delayed Response of Cross Section Area to Variable Incoming Flow and Sediment at Shashi Segment of Yangtze River
ZHANG Yun-chao1,LI Ling-yun1,2,FAN Bei-lin1,2,ZHENG Shan3
(1.River Department,Yangtze River Scientific Research Institute,Wuhan430010,China;2.Key Laboratory of River Regulation and Flood Control of MWR,Yangtze River Scientific Research Institute,Wuhan430010,China;3.School of Water Resources and Hydropower Engineering,Wuhan University,Wuhan430072,China)
Analysis on the measured flow and sediment data of the middle reaches of the Yangtze River as well as the section data indicates that the adjustment of channel morphology at Shashi station is delayed to the variation of flow and sediment conditions.In order to obtain the regularity of delayed response of Shashi section,we improved the delayed response model for river evolution in the Yellow River in three aspects:1)define the cross section area at the annual average low water level of Shashi section as the characteristic variable of the delayed response model;2)introduce the“yearly combined flow”;3)use the piecewise function in the iterative formula of the model.The results show that the determinant coefficient R2of delayed response model for river evolution at Shashi section is between 0.7 and 0.8.
alluvial river;river bed evolution;variations of incoming flow and sediment;delayed response;section area;Shashi station of Yangtze River
TV147
A
1001-5485(2016)07-0001-05
2015-04-21;
2015-05-13
国家自然基金项目(51209015,51339001);水利部公益性行业科研专项项目(201401011);湖北省自然科学基金面上项目(2014CFB329)
章运超(1990-),男,安徽池州人,硕士研究生,主要从事水力学及河流动力学研究,(电话)18507122759(电子信箱)zychao022@163.com。

