上荆江典型断面河床纵横向变形过程的概化模拟

张　翼，夏军强，邓珊珊，宗全利



上荆江典型断面河床纵横向变形过程的概化模拟

张翼1，2，夏军强1，邓珊珊1，宗全利1

（1．武汉大学水资源与水电工程科学国家重点实验室，武汉430072；2．浙江省水利河口研究院，杭州310020）

针对当前三峡工程运用后坝下游河床的调整特点，将床面冲淤与河岸崩退的计算模块相结合，构建了基于断面尺度的河床纵向及横向变形的概化数学模型。以上荆江荆34断面为研究对象，采用概化模型计算了该断面2006年和2008年水文年的河床纵向与横向变形过程，计算的河床纵向冲刷量、河岸崩退总宽度及崩塌后岸坡形态等结果与实测结果吻合较好。此外还分析了考虑与不考虑床面冲淤2种情况下2006年荆34断面形态调整的计算结果，该断面河床冲刷主要集中在枯水河槽，床面冲刷下切导致河岸高度增大，最大增幅约1．9 m，且考虑河床冲淤后计算的河岸崩退总宽度比不考虑时的计算值偏大20%。表明了近岸床面冲刷下切导致滩槽高差增大，将会加剧崩岸的发生。

上荆江河段；二元结构河岸；崩岸过程；纵向冲淤；概化模拟

doi：10．11988/ckyyb．20150352

1　研究背景

冲积河流在挟沙水流的作用下，河床总是处于不断的调整变化之中。河床变形在空间上可分为纵向变形和横向变形2种。纵向变形通常指床面的冲刷或淤积；横向变形一般指河岸的崩退或淤长［1］。三峡水库蓄水后，进入下游河道的水沙条件发生改变，使得上荆江河段河床形态发生相应调整，床面在持续纵向冲刷的同时，局部河段的河道崩岸过程也较为明显。实测资料统计表明：2002—2013年上荆江段河床累计冲刷量达3．9亿m3（平滩河槽），河床平均冲刷深度约1．6 m；上荆江沙市河段部分断面累计崩岸宽度达150 m［2］。崩岸不仅影响河道防洪安全，而且还会危及河势稳定及河道治理效果等。因此，针对三峡水库蓄水后上荆江河段河床的调整情况，开展典型断面河岸的崩退过程研究，有助于全面掌握该河段的河床演变规律，具有重要的意义。

上荆江河岸为上层黏性土、下层沙土组成的二元结构，且具有沙土层较低、黏性土层覆盖较厚等特点。受近期河床冲刷下切的影响，该河段河岸高度普遍增加、岸坡变陡，易引发崩岸险情。因此，研究崩岸时需考虑近岸河床的纵向冲淤变形等因素，而现有崩岸过程的概化模拟通常仅针对河床横向变形，很少将两者结合起来模拟其纵、横向变形过程。如王博等［3］以荆江段典型断面为研究对象，采用BSTEM模型分析了岸坡形态、水位条件等对河岸稳定性的影响；张幸农等［4］等采用室内概化试验与数值计算相结合的方法，分析了岸坡稳定或破坏的力学机制，揭示了长江中下游河段缓坡崩岸的原因。上述基于力学过程的河岸稳定性计算方法，能够较好地模拟河床横向变形，但忽略了河床纵向变形的影响，故在实际应用中具有一定局限性。近年来，随着泥沙数学模型的发展，平面二维模型已用于河道纵向与横向变形的计算。夏军强等［5］建立了正交曲线坐标系下的平面二维河床变形的混合模型，较好地模拟出了黄河下游游荡段非汛期槽淤滩冲与汛期槽冲滩淤的演变过程；假冬冬等［6］构建了考虑河岸变形的三维水沙模型，能够有效地模拟由河岸崩塌引起的河道横向摆动过程。但这些模型通常仅适用模拟均质黏性土河岸，不能计算二元结构河岸的崩退过程。此外，这些模型在河岸稳定分析中进行了大量的简化处理，认为河岸的崩塌模式为破坏面角度不变的平行后退，这与实际情况不符。

天然河道的河岸形态通常较为复杂且土体沿垂向往往具有分层结构，现有模型很少能适用于此类河床的纵向及横向变形过程计算。为此本文将非均质河岸崩退的力学模型与床面冲淤计算模块相结合，建立了基于断面尺度的河床纵向及横向变形的概化数学模型；然后结合上荆江河段的实测资料，对典型断面的河岸崩退及床面冲淤过程进行了模拟，并与实测结果比较；最后进一步分析了河床纵向变形对河岸稳定性的影响。

2　基于断面尺度的河床纵向及横向变形的概化模型

本文建立的河床纵向及横向变形概化模型，不仅能计算河床的垂向冲淤变化，而且能模拟非均质河岸的崩退过程，同时考虑了崩塌土体对坡脚的掩护作用。如图1所示，该模型首先采用水沙动力学方法计算左、右岸坡脚之间的床面冲淤变形过程；其次通过具有力学机理的河岸崩退模块计算坡脚以上的河岸变形过程。

图1　典型断面形态变化过程Fig．1　Change in the cross-sectional profile of a typical section

2．1河床纵向变形计算

荆江河段水文站及水位站点布设相对较多，一般可通过插值近似得到研究断面的逐日流量、含沙量及水位过程，并结合地形资料求解出断面内各节点的水流要素；在此基础上进一步求出分组水流挟沙力等；最后采用河床变形方程计算大断面总的垂向冲淤面积并等厚分配到各节点上。河床变形方程的具体形式为

式中：ρ'为床沙干密度（kg/m3）；Δt为时间（s）；ΔA0为总的河床变形面积（m2）；B为河宽（m）；N为非均匀沙的分组数；Sk，S*k分别为第k粒径组泥沙的含沙量及挟沙力（kg/m3）；αsk，ωsk分别为第k粒径组泥沙恢复的饱和系数及有效沉速（m/s）。其中总水流挟沙力采用张瑞瑾公式计算［7］。

2．2河床横向变形计算

本文借鉴BSTEM［8］模型的方法，将河床横向变形计算分为横向冲刷宽度及河岸稳定性计算2部分，分别用于模拟水流对河岸的侧向冲刷过程以及河岸土体的崩塌过程，如图2所示。

图2　河岸崩退过程计算Fig．2　Calculation of the erosion process of river bank

因天然冲积河流河岸沿垂向往往具有分层结构，故为了精确模拟河岸土体组成的不同特性，将河岸土体垂向分为5层。具体分层标准如下：首先将不同类型土体的分界面作为分层面1；由于潜水面以下土体处于饱和状态，与上部土体的物理力学特性不同，故潜水面作为分层面2；此外，除了上述确定的分层面，其它同一类型土体可根据厚度均匀分层详见图1。

2．2．1横向冲刷宽度

根据切应力差值法计算水流对河岸土体的横向冲刷宽度（图2（a）），即

式中：ΔB为横向冲刷距离（m）；K为冲刷系数（m3/ N·）；τ0为水流切应力（N/m2）；τc为河岸土体起动切应力（N/m2）。水流切应力可采用式（3）计算，即

2．2．2河岸稳定性

上荆江为上部黏性土层较厚、下部沙土层薄的混合河岸，当河岸坡脚或下层沙土遭到水流持续冲刷后，致使河岸变陡，上部土体易发生崩塌。当上部黏性土层厚度较大时，崩岸类型多为平面滑动［5］。为此本模型仅考虑崩岸类型为平面滑动的情况，通过计算潜在破坏面上土体的抗滑力FR与下滑力FD的比值，即为安全系数Fs。实际情况中，由于岸坡失稳时破坏面的位置难以确定，本文根据不同的基底高程与崩岸角度假定出多个崩岸破坏（见图2（b）），分别计算其安全系数Fs，其中Fs最小值对应的破坏面即为实际破坏面。F，F，F具体计算公式如下：

式中：Li为第i层土体中崩塌破坏面的长度（m），分别为第i层土体的有效凝聚力（kPa）及有效内摩擦角（°）；φib为第i层土体表观凝聚力随基质吸力增加而增加的快慢程度（°）；uai，uwi分别为第i层土体孔隙气压力及孔隙水压力（kPa）；Pi，Wi分别为第i层土体的侧向水压力及单位重力（kN/m2）；α为河岸坡度（°）；β为崩塌面角度（°）；imax为河岸崩塌土体总层数。

应当指出，由于上荆江二元结构河岸不同土层的抗冲性差异较大，上层黏性土受颗粒之间黏结力的影响，抗冲性较强。故发生崩岸时，上层崩塌的黏性土体并不会立刻全部被水流带走，部分土体将在坡脚形成堆积体，对覆盖的近岸河床起到掩护作用。为此，本文假定坍塌下来的上层黏性土体将按一定比例P（堆积系数）及β0（堆积角度）在坡脚处堆积。堆积系数P可根据水流条件确定：流速越大，水流对土体的冲刷作用越强，P值越小。

3　计算步骤

（1）初始条件输入，如初始断面地形及水沙条件、河岸各层土体厚度以及相应的土体力学性质指标、起动切应力等。

（2）计算河床纵向变形，并根据河床冲淤状况修改岸坡形态。如图2（c）所示，若近岸河床淤积，则岸坡形态由原始的 A—B—V—W变为 A—B—V1—W1，滩槽高差减小；若近岸河床冲刷，则岸坡形态变为A—B—V2—W2，滩槽高差增大。

（3）计算河岸横向冲刷宽度，如图2（a）。

（4）计算河岸安全系数Fs，并判断是否发生崩岸：若Fs＞1．3，表明河岸处于稳定状态；若Fs≤1．3，则河岸处于不稳定状态，发生崩岸，如图2（b）。

（5）依据河岸稳定性的判定结果，选择不同的计算步骤：若河岸稳定，返回第（2）步，开始下一时段的计算；若发生崩岸，则修改河岸形态并重新计算河岸坡脚位置，返回第（2）步。

（6）循环计算，直至结束。

4　模型应用

针对三峡水库蓄水后坝下游河段的实际冲刷情况，选取近期崩岸程度较严重的荆34断面作为研究对象。结合荆江段的实测资料，采用上述模型对该断面的河床纵向及横向变形过程进行模拟，并分析了近岸河床冲淤对河岸稳定性的影响。

4．1河段概况与计算条件

荆江河段位于长江中下游，上起枝城，下迄城陵矶，全长347．2 km，以藕池口为界分为上、下荆江。上荆江长171．7 km，为微弯分汊型河道，河岸大部分为土沙二元结构，抗冲性差，如图3所示。

图3　上荆江河段示意图Fig．3　Sketch of the upper Jingjiang Reach

选取了位于沙市河段荆34断面作为研究对象，采用该断面2006年及2008年水文年的实测资料分别对模型进行了率定和验证。计算中所需的流量、水位、含沙量及悬移质泥沙级配等资料等通过陈家湾站及沙市站的实测资料得到，土体凝聚力c、内摩擦角φ、密度ρ等，可由室内土工试验确定［10］，具体见表1。

表1　荆34断面右岸不同土层物理力学性质参数Table 1　Physico-mechanical parameters of different soil layers at the right bank of cross section Jing34

4．2河岸崩退过程计算

本次模拟的初始地形采用每年10月底荆34断面实测地形数据，故模拟的初始时刻为11月1日。同时根据长江中下游的流量及水位变化过程，进一步将率定过程（2005年11月1日至2006年10月31日）与验证过程（2007年11月1日至2008年10 月31日）分别划分为4个阶段：退水期（上年11月份至12月中旬）、枯水期（上年12月中旬至3月中旬）、涨水期（3月中旬至4月底）、洪水期（5月至10月底）［11］。

4．2．1模型率定及验证过程

随着河道内流量变化及水位涨落，上荆江河岸土体特性及近岸水流条件在一个水文年内呈周期性变化，从而使得河岸稳定性也随之变化。图4给出了模型计算的河岸稳定安全系数Fs的变化过程，不同时期计算结果分述如下。

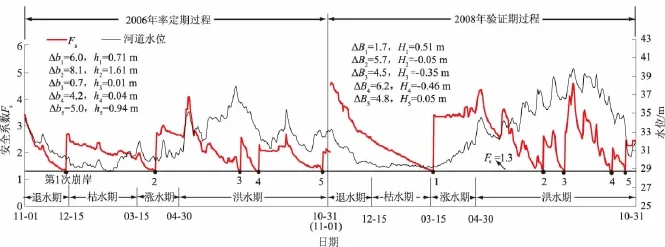
图4　荆34断面河岸稳定安全系数Fs值变化过程Fig．4　Temporal changes of safety factor Fsof river bank at the cross section Jing34

图5　率定过程退水期荆34断面右岸形态的变化过程Fig．5　Calculated profiles of the right bank at the cross section Jing34 in water recession period in calibration process

（1）退水期河道内水位急剧回落，水位下降使得作用于河岸外侧的水压力减小；此外，由于高水位对河岸土体的长时间浸泡，导致土体强度降低，都不利于河岸稳定性。率定过程中退水期发生了1次崩岸，其崩塌过程可分3个阶段：①随着坡脚处土体不断冲刷及下切，岸坡逐渐变陡、滩槽高差增大，河岸安全系数Fs由初始时刻（11月1日）的3．4逐渐减小，直至12月13日Fs=1．29＜1．3，发生第1次崩岸，崩岸宽度和体积分别为6．0 m及61．3 m3/m，而相应的坡脚横向冲刷距离及近岸河床冲刷深度分别为10．7 m和0．71 m，如图4，图5所示（图4中Δbi和hi分别为率定过程第i次崩岸时的崩岸宽度及河床平均冲刷深度（hi＞0冲刷，hi＜0淤积）；同样ΔBi和Hi为验证过程相应的崩岸宽度及冲刷深度）；②崩岸发生后岸坡形态变缓，河岸恢复稳定，同时崩塌土体堆积坡脚对近岸河床形成掩护（图5），使得水流对河床的冲刷有所减缓，Fs值增大至2．7；③随着坡脚处堆积土体被完全冲刷带走，则水流进一步冲刷河岸，Fs值逐渐减小直至＜1．3发生崩岸，之后河岸又进入了下一个从稳定趋向于不稳定的过程。由此可见，崩岸是水流淘刷河岸坡脚，岸坡变陡直至失稳及崩塌土体堆积坡脚并在河床上输移的反复循环过程。

（2）枯水期河道内流量及近岸流速均较小，近岸床沙处于未起动或少量起动状态。模型计算率定及验证过程中该时期平均近岸水流切应力τ0分别为1．4 N/m2及1．1 N/m2，大于下层沙土的起动切应力τc（0．06 N/m2），故河岸下部沙土层仍存在一定程度的横向冲刷。另外，期间河道来流含沙量总体上小于水流挟沙能力，故床面也处于冲刷下切的状态。然而，枯水期水流对河岸坡脚的冲刷程度较弱，故Fs值总体上处于缓慢减小的趋势，未有崩岸发生，如图4所示。应当指出，实际中个别岸段的近岸河床若在前阶段内遭受到较严重的冲刷，则有可能在枯水期发生崩岸；此外，渗流破坏引起浅层滑动也可能导致岸坡在枯水期失稳崩塌，但这2种情况发生的概率较低［11］。

（3）涨水期流量增加较快，近岸流速也明显增大，水流对坡脚的冲刷作用变强。由图4可见，水流对河岸的持续冲刷导致安全系数Fs逐渐减小，岸坡分别于2006年4月8日及2008年3月18日发生了8．1 m和1．7 m的崩岸，崩岸后河岸恢复稳定，Fs值增大。

（4）洪水期洪水峰高量大，持续时间长，水流对河岸的冲刷最强。率定及验证过程的汛期分别发生了3与4次崩岸，且这7次崩岸中有5次发生在河道水位迅速下降的阶段，如率定过程的第3、第4次崩岸以及验证过程的第3、第4、第5次崩岸，如图4所示。其中率定过程发生第3次崩岸后（7月11日），此时河道水位为37．9 m（未漫滩），Fs值为1．84，之后随着水位快速降低至7月18日的36．0 m，相应的Fs值迅速减小，仅为1．29（＜1．30），发生该水文年内的第4次崩岸。上述现象进一步表明了洪水期某些时段内河道水位的持续下降将导致河岸侧向水压力减小，使河岸稳定性明显下降，容易引起崩岸发生。

本文首先以荆34断面2005年10月实测断面形态为初始地形，对2006水文年的河床变形过程进行模拟，率定出模型中的泥沙恢复饱和系数及崩塌土体在坡脚处的堆积角度等参数，其中淤积恢复饱和系数与冲刷恢复饱和系数分别取0．25和1．05，崩塌土体堆积角度为20°。并将模型计算结果与2006年10月实测河床形态进行对比，如图6（a）所示。由图可见，随着河岸坡脚的淘刷，岸坡逐步向后崩退。率定过程中河岸崩退总宽度的计算值为24 m，实际值为21 m，两者误差不到15%；横向侵蚀量的计算值为457．4 m3/m（包括坡脚冲刷量与河岸崩塌量），实际值443．3 m3/m，两者误差仅3．2%；河床冲刷量的计算值（1 233．9 m3/m）与实际值（1 125．1m3/m）的误差不到10%。然后将率定后的模型参数应用于2008年水文年的河床形态调整过程的模拟，验证模型的适用性，从验证过程的计算结果来看（图6（b）），崩岸总宽度、横向侵蚀量以及河床冲刷量的计算值分别为22．9 m，605．7 m3/m，157．8 m3/m，相应的实际值分别为26．2 m，729．2 m3/m，141．9 m3/m，两者误差也较小。由此可见，率定过程及验证过程中计算的河岸崩退宽度、横向侵蚀量及河床冲刷量均能较好地与实际结果相符。另外，从图6中还可看出计算的最终岸坡形态均也与实测结果符合较好。

图6　荆34断面岸坡形态变化过程Fig．6　Calculated bank profiles at the cross section Jing34 during different stages

4．2．2河床纵向变形对河岸稳定性的影响

2006年水文年荆34断面河床冲刷幅度相对较大，故分别计算了该年考虑及不考虑河床冲淤变化时河岸的崩退过程，通过对比两者的差异，定量分析了河床冲淤变化对河岸稳定性的影响。具体结果如下：

图7给出了考虑及不考虑河床冲淤过程2种情况下河岸安全系数Fs以及平均河底高程Zb的变化过程。由图可见，退水期内，平均河底高程Z逐渐减小，河床处于冲刷状态，但冲刷幅度较小（平均冲刷深度仅为0．71 m），期间考虑河床冲淤计算的Fs值略小于不考虑的计算值，且岸坡于同一天发生第1次崩岸（图7）。然而，随着河床的进一步冲刷下切，平均河底高程Zb继续减小，滩槽高差增大，近岸河床下切对河岸稳定性的影响较为大。同一时刻有、无河床冲淤两种情况下计算的Fs值出现较为明显的差异，且前者小于后者，如图7所示。考虑河床冲淤变化时，岸坡于2006年4月6日发生第2次崩塌（Fs=1．26＜1．30），此时河床平均冲刷深度为1．61 m，而不考虑河床冲淤变化的岸坡仍处于稳定状态（Fs=1．83＞1．30）。由此可见，近岸河床冲刷将导致滩槽高差增大，不利于河岸稳定性。

图7　考虑与不考虑河床冲淤过程河岸安全系数变化Fig．7　Comparison of the simulated results of safety factor with and without the effect of riverbed deformation

如图8所示，2006水文年不考虑河床冲淤过程时计算的崩岸总宽度及横向侵蚀量分别为20 m和376．5 m3/m，均比实际值小。此外，计算结果表明该年断面河床冲刷主要集中在枯水期，平均冲刷深度最大值约1．9 m，且考虑河床冲淤过程后计算的崩岸总宽度比不考虑的计算值偏大了约20%，横向侵蚀量偏大了21．5%。计算结果进一步表明了床面冲刷下切将导致滩槽高差增大，不利于河岸稳定性。应当指出，虽然考虑河床冲淤计算崩岸宽度误差更大，但计算横向侵蚀量误差较小，且模拟最终岸坡形态更接近实际情况（图8），因此模拟崩岸时有必要考虑河床变形过程对河岸稳定性的影响，尤其在近岸床面冲刷程度比较严重时。

图8　考虑与不考虑河床冲淤岸坡形态计算结果对比Fig．8　Comparison of the simulated bank profile results with and without the effect of riverbed deformation

5结论

长江三峡水库蓄水运用后，引起水沙条件发生改变，坝下游河床形态调整明显，既有纵向下切又有横向展宽。但目前对荆江段河床纵向及横向变形的研究相对较少。本文构建了基于断面尺度的河床纵向及横向变形的概化数学模型，该模型由建立在力学基础上的河岸稳定模块和床面冲淤计算模块共同组成。并采用上荆江河段荆 34断面 2006年、2008年水文年的实测资料，对该模型进行了率定及验证。主要研究结论如下：

（1）2006年水文年（率定过程）中崩岸总宽度、横向侵蚀量及河床冲刷量的计算值分别为24 m，457．4 m3/m，1 233．9 m3/m，实际值分别为 21 m，443．3 m3/m，1 125．1 m3/m，两者误差较小，同样2008年水文年（验证过程）中相应的计算结果也与实际结果符合较好。表明本文建立的模型不仅能计算河床的纵向冲淤过程，而且能较好地模拟二元结构河岸的冲刷与崩塌过程。

（2）对比2006年考虑及不考虑河床冲淤变化2种情况下河岸崩退过程的模拟结果，结果表明：2006年该断面河床发生了一定程度的冲刷，且主要集中在枯水期，床面最大冲深约1．9 m，与不考虑河床冲淤过程相比，考虑后计算崩岸总宽度偏大20%，横向侵蚀量偏大21．5%，表明近岸河床冲深导致滩槽高差增大，将会加剧崩岸发生，尤其在近岸河床冲刷较为剧烈时。

［1］ 谢鉴衡，丁君松，王运辉．河床演变及整治［M］．北京：水利电力出版社，1989．

［2］XIA J Q，ZONG Q L，ZHANG Y，et al．Recent Adjustment in Reach-scale Bankfull Channel Geometry of the Jingjiang Reach owing to Human Activities［J］．Science China Technological Sciences，2014，57（8）：1490-1499．

［3］ 王博，姚仕明，岳红艳．基于BSTEM的长江中游河道岸坡稳定性分析［J］．长江科学院院报，2014，31（1）：1-7．

［4］张幸农，假冬冬，陈长英，等．渐进坍塌型崩岸的力学机制及模拟［J］．水科学进展，2014，25（2）：246-252．

［5］夏军强，王光谦，吴保生．游荡型河流演变及其数值模拟［M］．北京：中国水利水电出版社，2005．

［6］假冬冬，邵学军，王虹，等．考虑河岸变形的三维水沙数值模拟研究［J］．水科学进展，2009，20（3）：311-317．

［7］ 张瑞瑾，谢鉴衡，王明甫，等．河流泥沙动力学［M］．北京：水利电力出版社，1989．

［8］SIMON A，CURINI A，DARBV S E，et al．Bank and Near-bank Processes in an Incised Channel［J］．Geomorphology，2000，35：193-217．

［9］HANSON G J，SIMON A．Erodibility of Cohesive Streambeds in the Loess Area of the Midwestern USA［J］．Hydrological Processes，2001，15（1）：23-28．

［10］宗全利，夏军强，许全喜，等．上荆江河段河岸土体组成分析及岸坡稳定性计算［J］．水力发电学报，2014，33（2）：168-178．

［11］余文畴，卢金友．长江河道崩岸与护岸［M］．北京：中国水利水电出版社，2008．

（编辑：王慰）

Three Gorges Project，we developed a generalized mathematic model for predicting the longitudinal and lateral deformation of riverbed．The computational module of bed evolution is combined with that of bank retreat in this model．Taking cross-section Jing34 in the Upper Jingjiang Reach as a study object，we calculated the longitudinal and lateral deformation processes during the 2006 and 2008 hydrological years by using the generalized model．The predicated erosion volume of the riverbed，total bank retreat width and the failed bank profile were all in good agreement with the measured data．In addition，the effect of the riverbed evolution on the bank profile of cross-section Jing34 in 2006 was also investigated．Simulated results indicate that the position of river bed scouring is mainly concentrated in the low flow channel，and the maximum increase in height of river bank is about 1．9m induced by the river bed erosion．Moreover，the calculated total bank retreat width under the scenario with bed evolution is 20%greater than that under the scenario without bed evolution．Therefore，the bed evolution increases the relative bank height，which can reduce the safety factor of bank．

Generalized Simulation of the Longitudinal and Lateral Channel Evolution of Typical Section in the Upper Jingjiang Reach

ZHANG Yi1，2，XIA Jun-qiang1，DENG Shan-shan1，ZONG Quan-li1
（1．State Key Laboratory of Water Resources and Hydropower Engineering Science，Wuhan University，Wuhan 430072，China；2．Zhejiang Institute of Hydraulic&Estuary，Hangzhou310020，China）

According to the adjustment characteristics of the downstream riverbed of dam after the operation of the

Upper Jingjiang Reach；composite riverbank；bank retreat process；longitudinal erosion and deposition；generalized simulation

TV147

A

1001-5485（2016）07-0006-06

2015-04-26；

2015-05-25

国家自然科学基金项目（51579186，51339001）；长江科学院开放研究基金项目（CKWV2014204/KY）

张翼（1991-），男，河南信阳人，硕士研究生，研究方向为河流动力学，（电话）0571-86486165（电子信箱）zhangyi0224@whu．edu．cn。

夏军强（1974-），男，浙江绍兴人，教授，研究方向为河流动力学，（电话）027-68774302（电子信箱）xiajq@whu．edu．cn。