武汉市区土动力学参数统计分析

邢立，李　恒，李井冈

(1.中国地震局地震研究所 地震大地测量重点实验室，武汉　430071；2.武汉地震工程研究院有限公司，武汉　430071)



武汉市区土动力学参数统计分析

(1.中国地震局地震研究所 地震大地测量重点实验室，武汉430071；2.武汉地震工程研究院有限公司，武汉430071)

摘要：为探究武汉市区土体动力学参数特性，收集了武汉市区146个工程场地353个钻孔的资料，并结合在武汉地震工程研究院有限公司进行的土体动三轴试验结果，整理出武汉市区530组土样的动力学数据。筛选后，根据武汉市区土体性质及土层深度分布的具体情况进行分组，以统计均值的形式给出武汉市区6种典型土体在不同埋深下动剪切模量比G/Gmax和阻尼比λ的参考值，并以粉质黏土、黏土及淤泥质土为例，以拟合曲线的形式给出G/Gmax，λ随剪应变γ变化的平均曲线。通过与规范值、行业推荐值对比，得出武汉市区土体动剪切模量比受埋深影响相对较小，接近于行业推荐值，而阻尼比与规范值、行业推荐值相比大小关系不固定等结论。该结果可供武汉市区地震安全性评价工作和岩土地震工程应用参考使用。

关键词：动三轴试验；土动力学参数；动剪切模量比；阻尼比;土体性质；武汉市区

土动力参数中动剪切模量比G/Gmax和阻尼比λ，是场地地震安全性评价中土层地震反应分析的基本参数，其对地表峰值加速度、时程和反应谱计算的重要影响，已得到许多专家的验证[1-6]。在场地地震安全性评价工作中，常采用的《工程场地地震安全性评价工作规范》(1994)[7]，由于取样地区范围小，给出的G/Gmax-γ及λ-γ推荐关系代表性有限，为此，许多学者对特定地区常规土体[5-6,8-11]及特殊土体[12-13]的动力学参数的适用性进行了研究。袁晓铭等[14]2000年根据全国十几个地区常规土体的共振柱试验，给出了常规土动力学参数推荐值，但能否很好地适用于武汉市区尚未验证。此外，目前武汉地区对这种具有明显区域特性的土体动力学性质进行的系统研究还较少。本文将对武汉市区几种典型土体的动力学参数进行较为系统的统计及试验分析，并将分析结果与规范值[7]及推荐值[14]进行对比，分析武汉市区土动力学参数的特性，并给出参考值。

1土的动力学参数测定

1.1试验原理

根据试验得出的σd-εd关系，由式(1)确定相应的动弹性模量，由式(2)计算出相应的动剪切模量，由式(3)可得出阻尼作用等效滞回阻尼比λ，由式(4)计算出动剪应变γd。

(1)

(2)

(3)

(4)

式中：σd为动应力;εd为动应变;Ed为动弹性模量;ν为泊松比;A为滞回圈ABCDA的面积;As为三角形OAE的面积(图1)。根据试验数据，利用上述公式和最小二乘法进行回归分析，得出文中所用的试验数据。

1.2试验步骤

本文中所用的试验数据是由中国地震局工程力学研究所和中国地震局地震研究所测定给出的。其中，中国地震局地震研究所测定的部分，采用的是SDT-10微机控制电液伺服动态土工三轴测试系统。试验按《岩土工程勘察规范》GB 50021—2001和《土工试验规程》SL237—1999进行操作。

试验操作过程如下：

(1) 选用武汉市区有关工程场地勘探钻孔采集的原状土样，制备成几何尺寸为直径39.1 mm、高80 mm的标准土样。

(2) 将制备好的标准土样套上橡皮膜，排除土样与橡皮膜间的空气，并在土样上下表面垫好润湿的滤纸及透水石，用橡皮筋箍紧，使其密封在压力室内。

(3) 在固结比Kc为1.0的情况下，根据取样深度的不同，对试样施加相应的等向压力(0～5 m施加0.05 MPa，随后深度每增加5 m，固结压力增加0.05 MPa)，进行排水固结。

(4) 由微机控制，在不排水情况下对土样采用逐级循环加载的方式，施加设定级数、设定大小的动荷载。每级荷载连续观测5次，频率为1 Hz。

2土动力学参数统计

2.1统计区域

本文统计所用的数据，来自于武汉地震工程研究院有限公司，且所有数据均是近年来在武汉市区完成的。地震安全性评价报告中的土动力学试验数据具有完整性，即共353个钻孔、530组土样的土动力学数据，其中，笔者试验测定的有90组。这些钻孔，主要分布在长江、汉水两侧地带，基本上覆盖了武汉市的主城区(图2)。

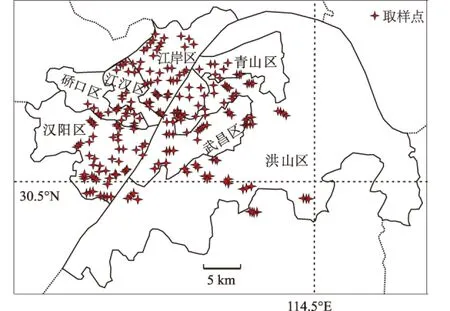
图2　研究区域范围及取样点分布

根据土的性质及密实度的不同，将其分为粉质黏土、黏土、松砂、中密砂、密砂、淤泥质土6类，其中，粉质黏土和黏土采样深度主要集中在5～25 m，淤泥质土取样深度主要集中在0～20 m，砂土取样深度主要集中在10～45 m。

2.2统计方法及统计样本量

为便于分析武汉市区土体动力学特征，现根据各类土的深度分布特征及土样埋深的不同，将其分成若干组(本文统计的6类土体共分18组)，并以选择标准差的形式剔除各组数据中动剪切模量比及阻尼比相对其对应“样本均值”离散较大的样本，以保证统计结果的合理性。经筛选，最终选定432 个样本的数据参与统计，各类土样样本量如表1。

表1　各类土样样本量统计Table 1　Statistics of soil samples

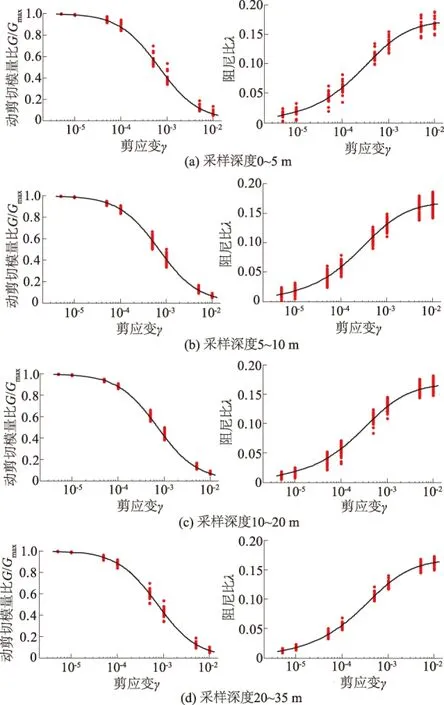
图3　不同深度范围内粉质黏土动剪切模量比和 阻尼比样本值的分布及平均值拟合曲线

对各组数据，以统计学方法给出其动剪切模量比及阻尼比的平均值。以粉质黏土为例，其动剪切模量比及阻尼比在不同深度范围内样本值的分布及其随剪应变变化的平均拟合曲线如图3。

表2　6类土体动剪切模量比与剪应变对应关系对比Table 2　Dynamic shear modulus ratio vs. shear strain for six types of soil

3成果及对比分析

3.1统计结果

按照2.2节所述的统计方法，对上述6类土体的动力学数据进行整理，得到6类土体不同深度范围内的动剪切模量比、阻尼比统计平均值。该结果和当前已有的行业规范及科研成果(《工程场地地震安全性评价工作规范》、袁晓铭等[14]2000年给出的推荐值)中给出的各类土体动剪切模量比、阻尼比与剪应变的对应关系对比值如表2、表3所示。

3.2统计值对比分析

由于规范值给出的土体动力学参数在埋深上不作区分，而袁晓明等给出的推荐值适用于埋深为0～10 m及10～20 m的土体，因此，本文根据武汉市区土体的埋深特点，选取了上述统计的6类土中埋深包括0～10 m及10～20 m的土体(粉质黏土、黏土、淤泥质土)，并给出了其动剪切模量比G/Gmax、阻尼比λ的统计平均值随剪应变γ变化的平均曲线(图4至图6)，以便更直观地比较本试验统计值与规范值、推荐值的异同。

文中所谓的“平均曲线”，即是将动剪切模量比和阻尼比统计平均值分别用Hardin等提出的动剪切模量比与剪应变关系式[15]及阻尼比与剪应变关系式的修正式[15]拟合。经检验，本文求得的统计平均值拟合曲线，在对应剪应变处的值与统计平均值的差值百分比小于4%，即|f(γ)-统(γ)|/ 统(γ)<4%。为保证对比结果的准确性及合理性，图中规范值和推荐值(袁晓铭等综合实验结果及经验给出的)不能用上述曲线极好给出的部分区段(如淤泥质土动剪切模量比在剪应变γ>10-3部分)，则以折线的形式给出。

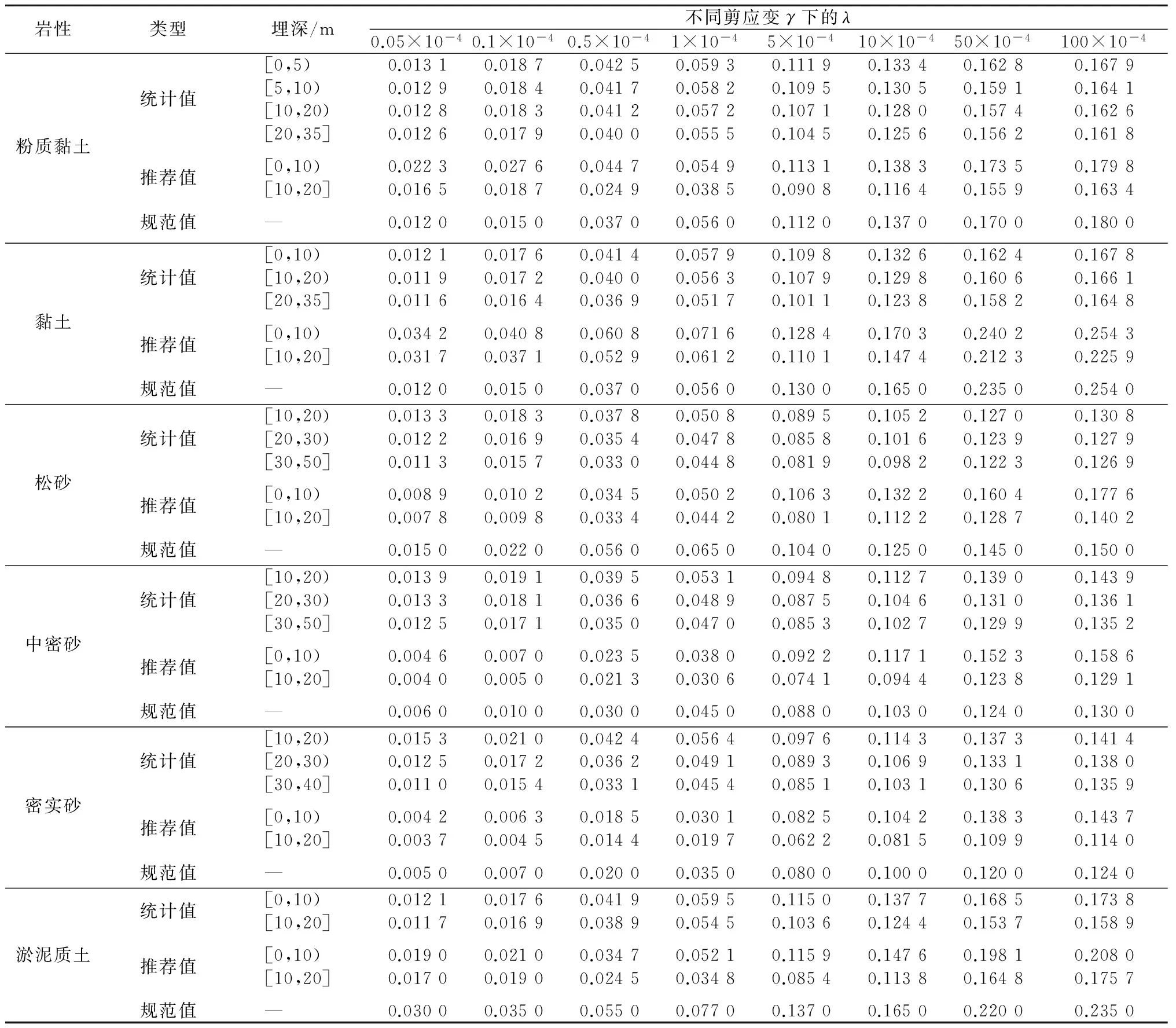
表3　6类土体阻尼比与剪应变对应关系对比Table 3　Damping ratio vs. shear strain for six types of soil

图4　粉质黏土动剪切模量比及阻尼比对比

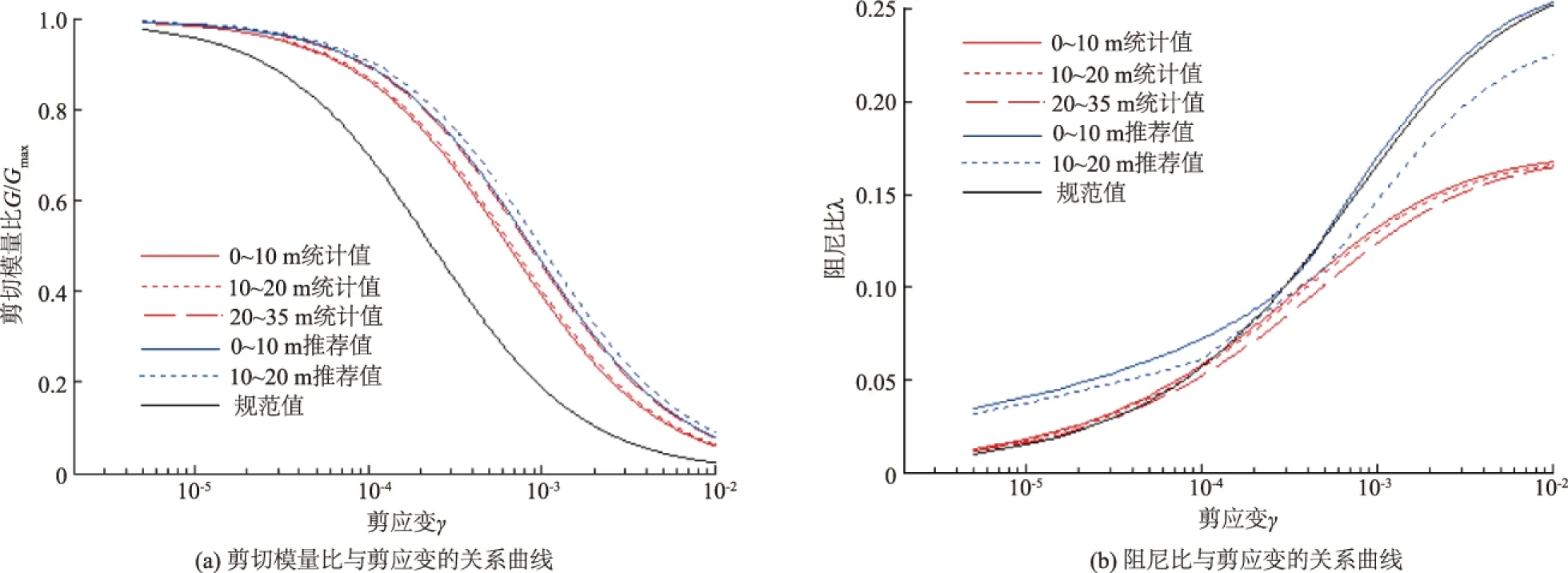
图5　黏土动剪切模量比及阻尼比对比

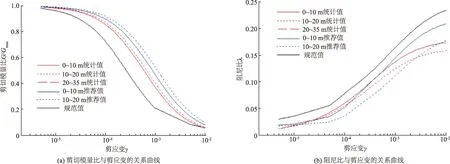
图6　淤泥质土动剪切模量比及阻尼比对比

从表2、表3和图4至图6可以看出，与袁晓铭等给出的推荐值及规范值相比，武汉市区的土体动力学参数总体水平与袁晓铭等给出的推荐值更为相近。但在动剪切模量比G/Gmax和阻尼比λ随剪应变γ变化的幅度上，武汉市区土体又有其明显特殊性。

(1) 武汉市区各类土体的动剪切模量比和阻尼比统计值与相应土体的推荐值相比，对埋深的敏感性较低，例如，埋深为0～10 m与20～35 m的粉质黏土，动剪切模量比和阻尼比统计值相差最大处均未超过对应点较大值的6%，而埋深为0～10 m与10～20 m的动剪切模量比推荐值相差最大处已达14%，阻尼比相差最大处更是高达40%以上。

(2) 武汉市区各类土体动剪切模量比总体水平更接近袁晓铭推荐值，皆高于规范值甚多，且除松砂和中密砂外，均略低于相应埋深的袁晓铭推荐值。对于阻尼比，3种值的大小关系及随剪应变的增长速率不固定，但总体上，当应变较小时，不同埋深各类土体的阻尼比统计值随剪应变的增长速率大于相应埋深的推荐值，此趋势与此应变范围内规范值的变化趋势更为接近，当应变较大时，不同埋深各类土体的阻尼比统计值随剪应变的增长速率小于规范值及相应埋深的推荐值。

4结语

本文通过对武汉地震工程研究院有限公司近几年在武汉市区完成的地震安全性评价项目相关资料的分析，结合在武汉地震工程研究院有限公司土动力实验室进行的土体动三轴试验，整理出武汉市区多种土体的动力学数据，经过筛选、统计等处理，给出武汉市区6种主要土体在不同埋深范围内的动剪切模量比、阻尼比的统计值，以及粉质黏土、黏土及淤泥质土的动剪切模量比、阻尼比统计平均值随剪应变变化的拟合曲线。

从6种不同岩性土体动力学参数统计值表2、表3可以看出列出的各类土体动力学参数与规范值和推荐值的差异。从给出的3类土体动力学参数平均变化曲线图4至图6可以看出，武汉市区各类土体动剪切模量比及阻尼比对埋深的敏感性较低，其中动剪切模量比更接近于相应的推荐值，且高于规范值甚多，因此，在武汉市区实际应用中应根据客观条件优先选用实测值、统计值、经适当修正的袁晓铭推荐值，如需使用规范值，则应根据情况适当提高。对于阻尼比，当剪应变较小时，优先选用实测值和统计值，规范值及袁晓铭推荐值应慎用，尤其是剪应变较大的情况下。

本文根据武汉市区各类型土体的埋深分布特征，对不同土体的动力学参数在埋深上进行了单独划分，与在埋深上不做区分的规范值和仅适用于2种埋深范围的袁晓铭推荐值相比，这种划分更符合武汉市区土体埋深分布的具体情况，并且试验所用土样的数量大，取样点分布密集，区域代表性强，能够更真实可靠地反映武汉市区土体动力性能的实际情况，得出的数据会更适合在武汉市区相关工作中参考使用。

参考文献：

[1]张小平，牛雪，赵安生，等. 大连地区场地土动力学参数初步研究[J]. 中国地震，2011， 27(3)： 280-289.

[2]孙静，袁晓铭，孙锐. 土动剪切模量和阻尼比的推荐值和规范值的合理性比较[J]. 地震工程与工程振动，2004，24(2)： 125-133.

[3]王绍博，丁海平.土动力参数对土层动力反应的影响[J].地震工程与工程振动，2001，21(1)：105-108.

[4]吕国军，田丽，张合，等.土层动力参数变化对地表地震反应影响的研究[J]. 华北地震科学，2013，31(2)：18-22.

[5]蒋其峰，彭艳菊，荣棉水，等.渤海海域粉质粘土动力学参数的统计分析[J].震灾防御技术，2014，9(2)：252-262.

[6]史丙新，张力方，吕悦军，等.天津滨海场地土动力学参数研究[J]. 震灾防御技术，2010，5(3)：288-298.

[7]DB001—94，工程场地地震安全性评价工作规范[S].

[8]兰景岩，刘化涤，吕悦军，等.渤海海域典型场地土的动剪切模量比和阻尼比的统计值[J], 地震研究，2012，35(2)：260-266.

[9]施春花，吕悦军，彭艳菊，等.北京地区粉质粘土土动力学参数的统计分析[J].震灾防御技术，2009，4(1)：69-78.

[10]陈国兴，刘雪珠，朱定华，等.南京新近沉积土动剪切模量比与阻尼比的试验研究[J]. 岩土工程学报，2006，28(8)：1024-1027.

[11]王炳辉，陈国兴，王晶华. 宁波近海沉积土动力特性的试验研究[J]. 自然灾害学报，2007，16(4)：56-60.

[12]骆亚生，田堪良. 非饱和黄土的动剪模量和阻尼比[J]. 水利学报，2005，36(7)：830-834.

[13]赵淑萍，朱元林，何平，等. 冻土动力学参数测试研究[J].岩石力学与工程学报，2003，22(2)：2677-2681.

[14]袁晓铭，孙锐，孙静，等. 常规土类动剪切模量和阻尼比试验研究[J]. 地震工程与工程振动，2000，20(4)：133-139.

[15]HARDIN B O, DRNEVICH V P. Shear Modulus and Damping in Soils Design Equations and Curves[J]. Journal of Soil Mechanics and Foundation, ASCE, 1972, 98(7): 667-692.

(编辑：赵卫兵)

收稿日期：2014-10-27; 修回日期:2014-11-26

基金项目：中国地震局地震科技星火计划项目(XH15027);中国地质调查局基础专项(1212011120097)

作者简介：邢立辉(1987-)，男，黑龙江七台河人，硕士，主要从事地震工程、岩土工程工作，(电话)15527242330(电子信箱)xinglihuicug@163.com。

doi:10.11988/ckyyb.20140907

中图分类号：P315.9

文献标志码：A

文章编号：1001-5485(2016)04-0061-06

Statistical Analysis of Soil Dynamics Parametersin the Urban Area of Wuhan

XING Li-hui1,2，CHEN Shu-jun1，LI Heng1,2，LI Jing-gang1

(1.Key Laboratory of Earthquake Geodesy, Institute of Seismology of China Earthquake Administration, Wuhan 430071, China； 2. Wuhan Institute of Earthquake Engineering Co., Ltd.， Wuhan430071, China)

Abstract:In order to explore the features of soil dynamics parameters, first we sorted out 530 groups of soils dynamic data by collecting data obtained from 353 boreholes in 146 sites as well as the results of dynamic triaxial test in the urban area of Wuhan. Then, we classify the data into groups according to soil properties and depth distribution of soil layer. Furthermore, we give the statistical mean value of dynamic shear modulus ratio and damping ratio of 6 typical soils. We take silty clay, clay and mucky soil as examples to present fitted curves of dynamic shear modulus ratio vs. shear strain and damping ratio vs. shear strain. Through comparison with code values and recommended values, we conclude that dynamic shear modulus ratio is limitedly affected by embedded depth, near to recommended value, whereas relationships among damping ratio of urban area in Wuhan, code value and recommended value are undetermined. The research results can be used as reference for evaluation of seismic safety and application in geotechnical seismology engineering.

Key words:dynamic triaxial test; soil dynamics parameters; dynamic shear modulus ratio; damping ratio; soil properties;urban area of Wuhan

2016,33(04):61-66