反例在与周期函数相关论断中的应用

◇　新疆　杜学忠



反例在与周期函数相关论断中的应用

◇新疆杜学忠

函数的周期性是函数的初等性质,在数学中周期函数有它特殊的用途．然而,对周期函数的学习,并没有专题的、深入的章节专门研究,使得很多与周期函数相关的论断让读者容易混淆.本文将列举一系列与周期函数相关的论断,并给出相应的反例,予以澄清．

定义函数f(x)定义在数集A上．若∃T>0,∀x∈A,有x±T∈A,且 f(x±T)=f(x),则称函数f(x)是周期函数,T称为函数f(x)的一个周期．若函数f(x)有最小的正周期,通常将这个最小正周期称为函数f(x)的基本周期,或称最小正周期．

问题1还有周期函数没有最小正周期的吗?

回答是肯定的,如常值函数y=c,c为常数;任何正实数都是它的周期,但没有最小正实数,所以它没有最小正周期.又如定义在整个数轴上处处不连续的Dirichelet函数

任一有理数r>0均是它的周期,但没有最小正有理数,所以它没有最小正周期．

问题2如何求2个周期函数的和函数的最小正周期?

对于这个问题,我们一般的做法:设函数f(x)的周期是T1,函数g(x)的周期是T2,则f(x)+g(x)的周期是T1与T2的最小公倍数．

于是,它的最小正周期是20π．

这个做法,看起来是没有问题的,但仔细一看,存在下列3个方面的问题:

1) 周期不一定是整数.

最小公倍数是2个整数的正公倍数中的最小者,而函数的周期不一定是整数,所以谈不上公倍数．

2) 这种方法本身就是错误的．

|sin(x±T)|+|cos(x±T)|=|sinx|+|cosx|,

|sin(x±T)cos(x±T)|=|sinxcosx|.

|cosx|+|sinx|=|sinx|+|cosx|．

图1

图2

图3

由图可知f(x)、g(x)的最小正周期都是2,但f(x)+g(x)的最小正周期却为1,很显然1不是2的最小公倍数,所以上述作法显然不对．

这个例子还可以推广,比如在图3中,每隔5拱,拿1拱,可构造出2个周期为6的周期函数,以此类推,我们可以构造2个周期为2、3、4、…的周期函数,但它们的和函数的周期仍为1．若一拱所对应的区间长是数a,则可以构造2个周期为2a、3a、4a、…的周期函数,但它们的和函数的周期仍a．图形也可以有所变化．

3) 2个周期函数的和不一定是周期函数.

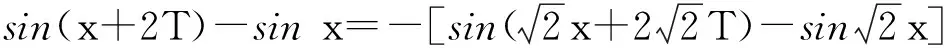
结论若f(x)与g(x)都是定义在D的周期函数,周期分别是T1与T2,且T1/T2=r,r是有理数,则f(x)+g(x)与f(x)g(x)都是D上的周期函数．

函数f(x)与g(x)都是定义在D的周期函数,周期分别是T1与T2,列表反映周期函数和的周期性情况(如表1).

表1　周期函数和函数的周期性情况

从表1可以看出,2个周期函数的和函数是否是周期函数,我们应该去求它们周期的商是否为有理数,若不是有理数,可以判定和函数不是周期函数;若是有理数,我们也不能直接求出它们周期的最小公倍数,就认为是和函数的最小正周期，而应该多方面考虑,如作出和函数的图象等再得出正确的结论．

总之,关于周期函数的更多讨论,读者可以参考其他文献资料,本文仅仅讨论了常见而又容易混淆的周期函数相关的论断，目的是为避免犯不应该犯的错误．

新疆塔城地区和丰县第二中学)