连续波雷达精度对初速试验估计的影响*

孔　伟,曾　荣,杜金玉,王卫欣

(中国华阴兵器试验中心,陕西华阴　714200)



连续波雷达精度对初速试验估计的影响*

孔伟,曾荣,杜金玉,王卫欣

(中国华阴兵器试验中心,陕西华阴714200)

摘要:炮口初速本质上是一个随机变量,需要射击一定数量的弹丸才能确定置信区间及置信度,连续波雷达作为测量初速的重要设备,其精度影响初速试验估计的用弹数量,文中对初速测量进行参数估计,计算初速置信区间及其置信度,并考虑雷达测速误差对初速估计的影响,讨论射弹数量与雷达精度的关系,以期选择最少的用弹量准确考核被试弹药性能,降低试验成本,提高试验效率。

关键词:初速;随机变量;置信区间;置信度;连续波雷达;精度;参数估计

0引言

弹丸的炮口初速是用经典的内弹道学理论研究火炮膛内动态过程的重要参数,是衡量火炮、弹丸和火药装药性能的一个主要标准[1]。

内弹道射击过程实质上是一个随机过程[2],炮口初速本质上是一个随机变量,试验中需要射击一定数量的弹丸,才能确定初速均值及标准差的置信区间及置信度。

连续波测速雷达的测量误差[3]不可避免地影响到初速的置信估计,其精度影响试验用弹数量,为减少武器弹药消耗,测量中必须了解雷达精度与射弹数量之间的关系。

为此,文中对初速测量进行参数估计,以期选择最少的用弹量准确考核被试弹药性能,降低试验成本,提高试验效率。

1正态分布均值与标准差的置信区间

(1)

(2)

在总体标准差未知时求解正态均值的置信区间,可以用样本标准差S去估计总体标准差σ,利用图1所示的t分布[5]。

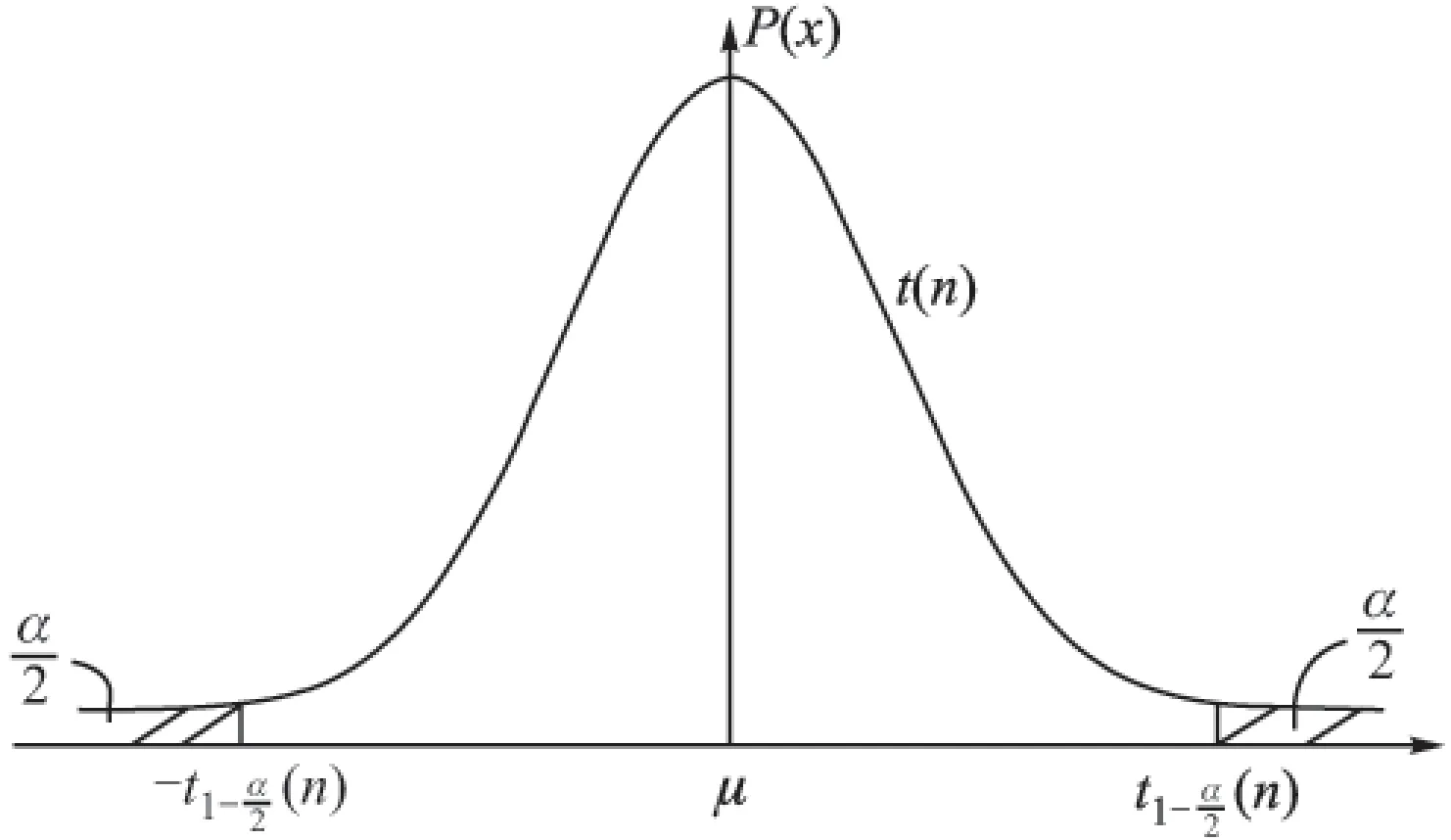
图1　t分布的密度函数与置信区间

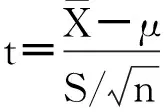
(3)

在总体均值未知时求解总体方差的置信区间,可从方差σ2的估计S2出发,利用图2所示的χ2分布[4]。

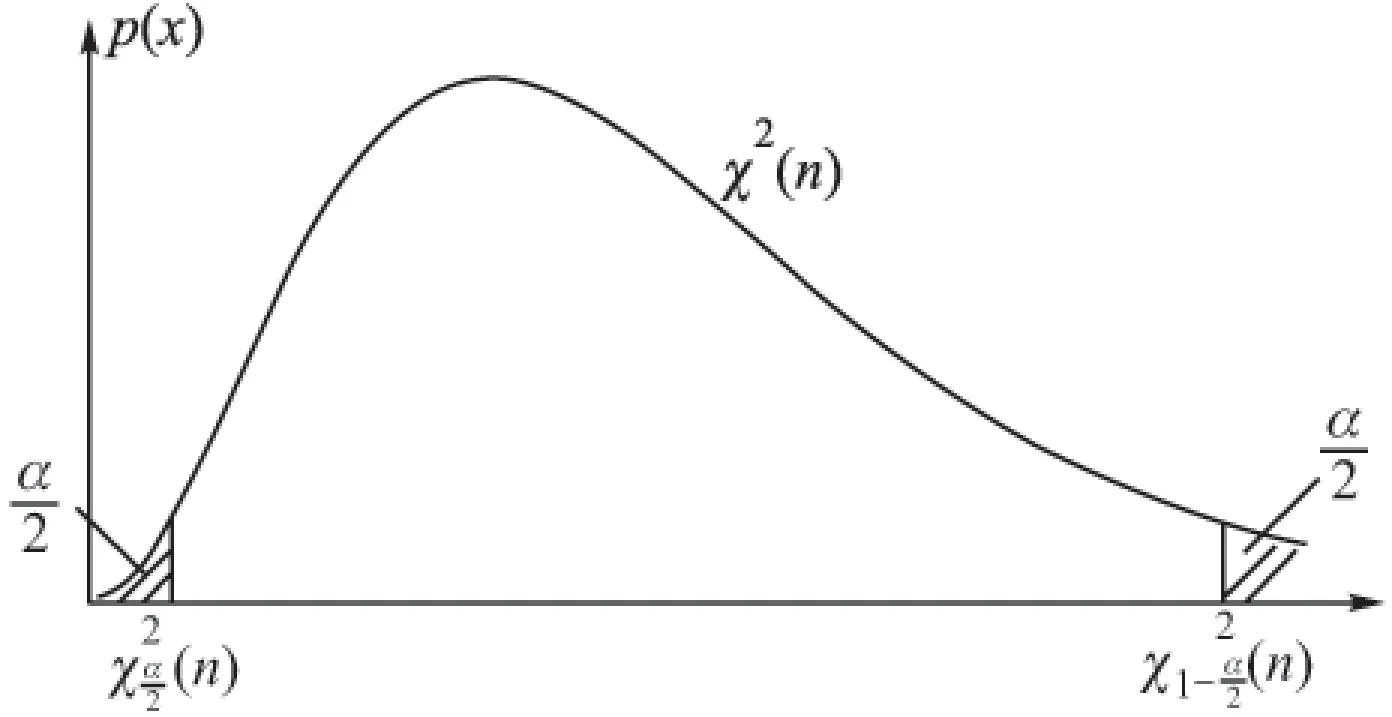
图2　χ2分布的密度函数与置信区间

标准差σ的1-α置信区间为:

(4)

当获得样本观察值x1,x2,…,xn后,由式(1)、式(2)可计算均值与方差,由式(3)、式(4)可计算均值置信水平为1-α的置信区间及方差的置信上限。

2初速的置信估计

试验中被试弹药的初速可以认为服从正态分布,雷达测量的一组初速v01,v02,…,v0n可以作为该批弹药的一个简单随机样本,代入式(1)、式(2)计算一组弹丸的平均初速及标准差:

2.1初速均值的置信区间

令

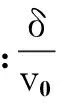
根据GJB2973A—2008火炮内弹道试验方法规定,弹丸速度在200～3 000m/s时,初速测量雷达最大允许测量误差为±0.1%。

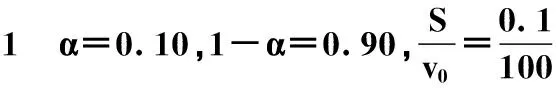
表计算结果

表计算结果

由表中给出的计算结果可知:

2.2初速标准差的置信上限

对一批弹药而言,初速样本方差满足:

根据式(4),在1-α=90%及95%两种情况下,计算初速标准误差的置信上限。

表3　α=0.10,1-α=0.90计算结果

由表3知,当要求标准差置信上限≤2S时,射击5发即可。

表4　α=0.05,1-α=0.95计算结果

由表4知,当要求标准差置信上限≤2S时,射击7发即可。

可见,测量一批弹药的初速,必须至少进行5(或7)发射击试验,初速标准差置信上限≤2S的概率为90%(或95%)。

3雷达误差对初速估计的影响

3.1雷达测速误差对初速均值估计的影响

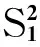
设雷达测速误差比弹丸初速误差小A倍,即:

则

计算A取不同值时,S′、n′及δ′/v0的值见表5。

表5　α=0.10,基本试验发数n=5的计算结果

由表5可知,如果测速雷达精度不高,A=1,雷达测速误差和弹丸初速误差一样大,需多打3发弹,才能达到要求的置信概率和置信区间;如果雷达测速误差比初速误差还大,A=0.5,则需多打11发弹,这种情况造成过大的人力、物力消耗,应是不允许的;如果雷达精度较高,A≥3,则不需增加试验次数;A=2,仅需多打1发弹,也是可以接受的。

表6　α=0.05,基本试验发数n=7的计算结果

由表6结果可以进行与表5类似的讨论,不同的是,后者的置信概率要求较高,在雷达精度较低时,要求增加更多的试验次数。

根据表5、表6数据作出射弹数量与雷达精度关系曲线如图3所示。

图3　射弹数量与雷达精度关系曲线

3.2雷达测速误差对初速标准差估计的影响

在估计初速标准差时,同样需要考虑雷达测速误差的影响。

表7　α=0.10,n=5,σU≤2S计算结果

表8　α=0.05,n=7,σU≤2S计算结果

根据表7、表8数据作出射弹数量与雷达精度关系曲线如图4所示。

图4　射弹数量与雷达精度关系曲线

4结论

参考文献:

[1]李益民. 弹道测量雷达及在兵器试验中的应用 [M]. 北京: 国防工业出版社, 2010: 105-117.

[2]冯德成, 翁春生. 随机内弹道学研究综述 [J]. 弹道学报, 2003, 15(1): 93-96.

[3]罗兵, 邓荣. 初速对射击精度的影响及测速雷达在舰炮武器系统中的应用 [J]. 舰船电子工程, 2014, 34(02): 74-75.

[4]茆诗松, 周纪芗. 概率论与数理统计 [M]. 2版. 北京: 中国统计出版社, 2000: 240-256.

[5]张志涌. 精通MATLAB6.5版 [M]. 北京: 北京航空航天大学出版社, 2003: 141-149.

*收稿日期:2015-03-22

作者简介:孔伟(1967-),男,山东曲阜人,高级工程师,硕士,研究方向:雷达测量及信号处理。

中图分类号:TN953.1

文献标志码:A

InfluenceofAccuracyofContinuousWaveDopplerRadaronMuzzleVelocityEvaluation

KONGWei,ZENGRong,DUJinyu,WANGWeixin

(HuayinOrdnaceTestCenterofChina,ShaanxiHuayin714200,China)

Abstract:Muzzle velocity is essentially a random variable measured in conventional weapon testing domain, confidence interval and confidence level of muzzle velocity are calculated by firing a quantity of projectiles, as main equipment, accuracy of continuous wave Doppler is an important factor influencing quantity of projectiles used in test range. Muzzle velocity was evaluated in this paper, confidence interval and confidence level were calculated, and error of measurement of the radar was evaluated for velocity accuracy, the relation between quantity of projectiles and radar measurement accuracy was discussed in order to cut down consumption of projectiles, and increase efficiency of firing accuracy measurement, the minimum projectiles were fired for evaluating ammunition.

Keywords:muzzle velocity; random variable; confidence interval; confidence level; continuous wave Doppler radar; accuracy; estimation of parameter