高速旋转弹载体干扰磁场补偿算法*
龙达峰,刘 俊,2,张晓明,李 杰
(1 中北大学电子测试技术国家重点实验室,太原 030051;2 中北大学仪器科学与动态测试教育部重点实验室,太原 030051)
高速旋转弹载体干扰磁场补偿算法*
龙达峰1,刘俊1,2,张晓明1,李杰1
(1中北大学电子测试技术国家重点实验室,太原030051;2中北大学仪器科学与动态测试教育部重点实验室,太原030051)
摘要:为解决高速旋转弹载体磁场会严重影响捷联地磁传感器的测量精度问题,文中在对弹体的载体干扰磁场机理分析与误差建模基础上,提出了基于Kalman滤波技术的弹体载体磁场误差参数估计与补偿方法。最后以152 mm旋转弹药载体磁场为研究仿真对象,对所述载体磁场补偿方法进行了算法仿真验证,结果表明该算法可有效实现载体磁场误差参数的准确估计,且地磁传感器测量数据在经误差补偿后,其测量精度提高一个数量级。
关键词:地磁传感器;载体干扰磁场;磁测补偿算法;高速旋转弹
0引言
地磁场信息的准确获取是实现高精度地磁导航的前提[1-2]。在地磁导航时,捷联于高速旋转弹的三轴地磁传感器实时测量高速旋转弹内的地磁场矢量信息。实际上,捷联地磁传感器测量输出信息不仅包括磁测解算所需的地磁场信息,还包括高速旋转弹载体内各种干扰源产生的有害磁场信息[3-5]。载体干扰磁场主要由高速旋转弹载体中的硬磁材料、软磁材料磁化而产生固定磁场、感应磁场和涡流磁场,或者由高速旋转弹内通电导体产生的干扰磁场[6-9]。若高速旋转弹载体干扰磁场达到上千纳特甚至更多时,其将会极大的降低捷联地磁传感器的信噪比,进而造成大的磁测解算误差[9]。针对载体磁场补偿问题,通常采用椭圆约束方法、十二位置标定法、干扰参数辩识法,或是最小二乘补偿等干扰磁场补偿方法[6-12]。但上述方法推导时主要考虑的是在静态情况下软磁和硬磁场补偿问题,特别对载体高机动状态下的涡流磁场等并没有进行讨论,因此所述磁场补偿方法存在一定的局限性,并不能完全满足高精度应用测量场合。为进一步提高地磁传感器的测量精度,文中对载体干扰源进行重新的分析与建模,并采用基于卡尔曼滤波技术对载体干扰磁场相关误差参数进行滤波估计以及磁测数据的在线补偿,以期减小载体干扰磁场对捷联地磁传感器的测量数据的影响,从而实现地磁场信息的准确获取。
1载体磁场数学模型
文中以高速旋转弹药地磁导航为研究对象,根据高速旋转弹载体干扰磁场源的不同,载体磁场可分解为固定磁场、感应磁场和涡流磁场。下面对其产生机理和形成原因作详细分析,建立各干扰磁场的数学模型。
1.1固定磁场模型[3,6,9]
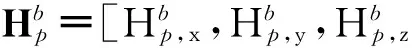
(1)
1.2感应磁场模型
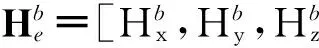
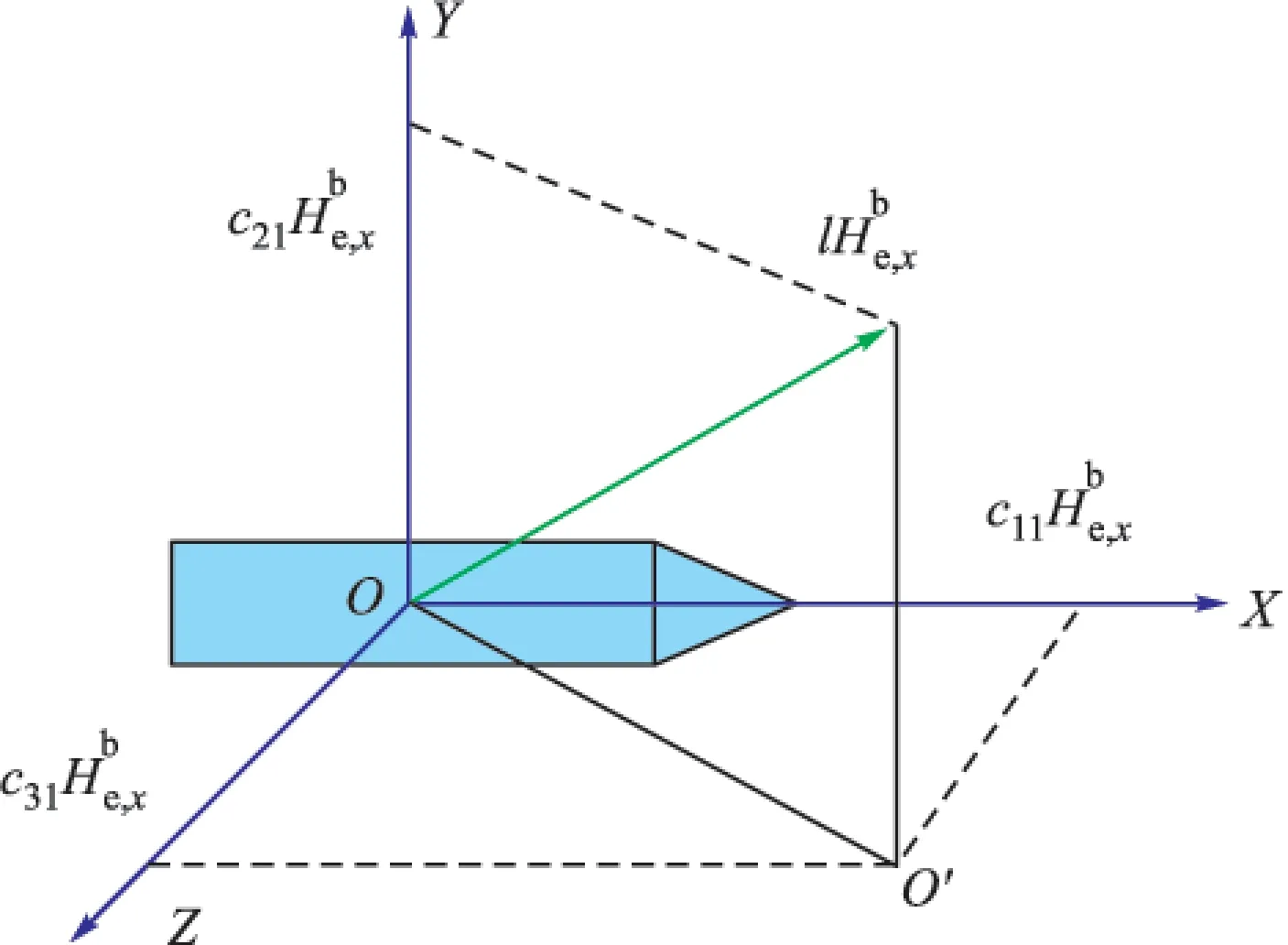
图1 弹体软磁感应磁场示意图
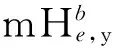
(2)
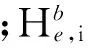
1.3涡流磁场模型
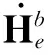
(3)
式中bij(i,j=1,2,3)为载体的涡流磁场磁化系数。
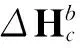
(4)
式中矩阵B和C为载体干扰磁场系数矩阵。
当地磁传感器捷联于高速旋转弹时,若不考虑各种测量误差,其理想测量输出为:
(5)
(6)
式中:ωi(i=x,y,z)为载体系内高速旋转弹的角速率,其可以通过捷联载体的三轴向陀螺仪测量得到。
将式(6)代入地磁传感器测量输出方程式(4),得到高速旋转弹干扰磁场的补偿公式为:
(7)
若能确定上述载体的干扰磁场各误差参数,则按式(7)可以实现载体干扰磁场的误差补偿。
2载体干扰磁场误差参数滤波器设计


(8)
式中:w(t)为系统过程高斯白噪声,且其满足
E[w(t)]=0,E[w(t),wT(τ)]=Q(t)δ(t-τ)。
将地磁传感器的测量输出模型(4)改写为:
(9)
若将式(9)中的方程左边的差值项作为滤波器
的量测变量Z(t),则方程(9)即可作为滤波器的观测方程:
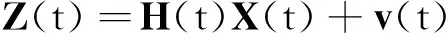
(10)
式中:v(t)为观测高斯白噪声,且其满足E[v(t)]=0,E[v(t),vT(τ)]=R(t)δ(t-τ)。
因此,综合上述状态方程(9)和观测方程(10)共同构成了系统的滤波模型,对其进行离散化处理可得:
(11)
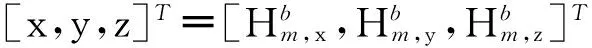
因此,基于Kalman滤波器的高速旋转弹载体干扰磁场误差参数滤波算法包括下列两个递推过程:
1)时间更新过程
(12)
2)量测更新过程
(13)
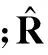
3算法的仿真验证
文中以152mm旋转弹药为仿真对象,根据外弹道6D数学模型,利用Matlab程序计算机仿真生成捷联于弹体的地磁传感器理想输出,然后加入载体干扰磁场仿真生成包括各种干扰源产生的有害磁场信息的实际磁测输出数据。在此基础上进行文中所述滤波补偿算法的计算机仿真验证。
3.1仿真参数设置
如上所述仿真生成的实际磁测输出数据中,载体干扰磁场误差参数、地磁传感器和陀螺仪传感器测量噪声设定如下:
2)载体干扰磁场系数矩阵B和C大小分别为:


3)三轴地磁传感器噪声分量大小为:[51,51,51]TnT。
4)三轴陀螺仪随机漂移噪声均为1°/h。
3.2仿真结果
在进行计算机仿真分析时,滤波器以200Hz频率进行量测数据更新。载体固定磁场、感应磁场和涡流磁场误差参数滤波估计结果如图2~图8所示。
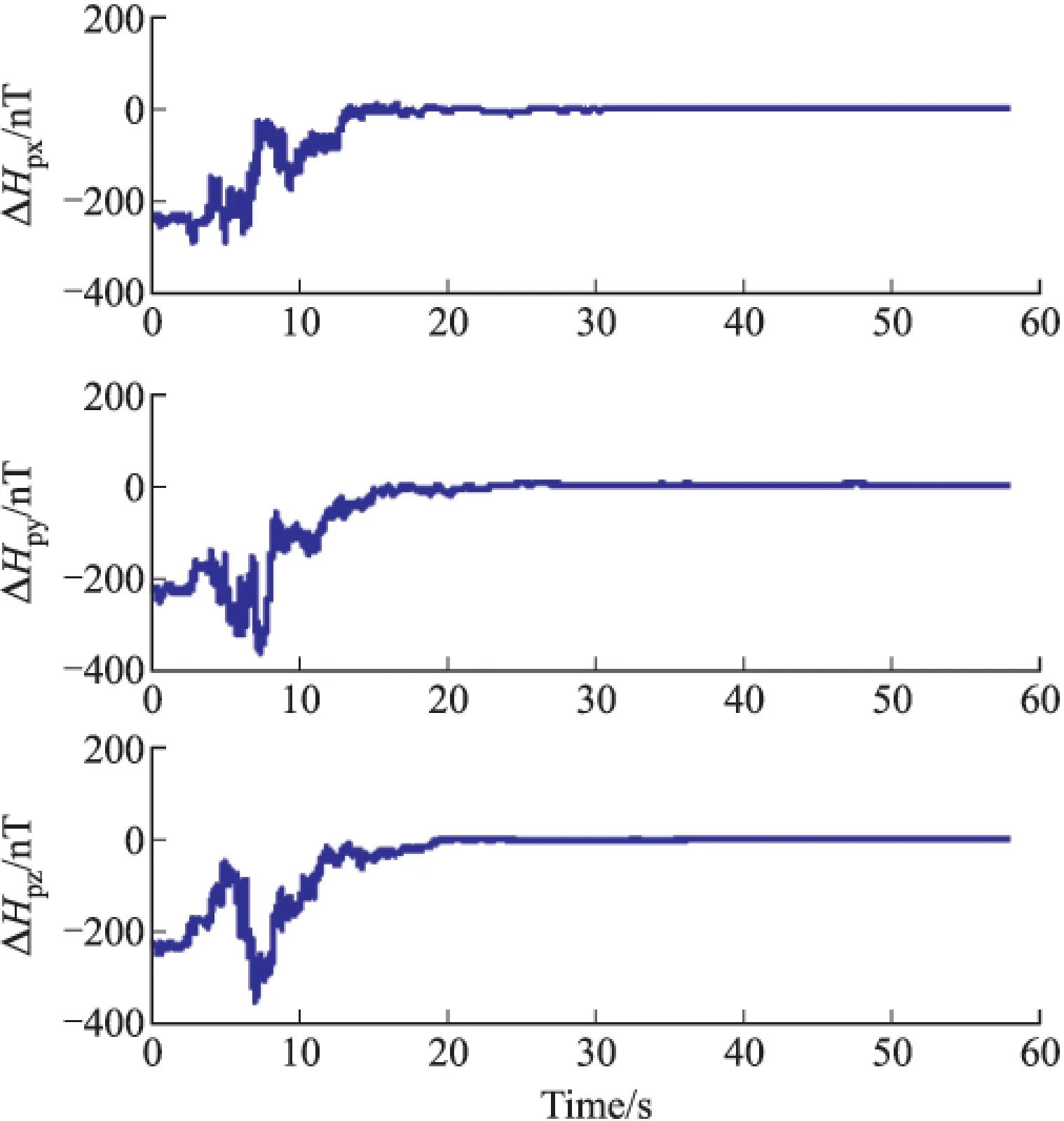
图2 固定磁场估计误差收敛曲线

图3 磁化系数c1j(j=1,2,3)误差收敛曲线

图4 磁化系数c2j(j=1,2,3)误差收敛曲线
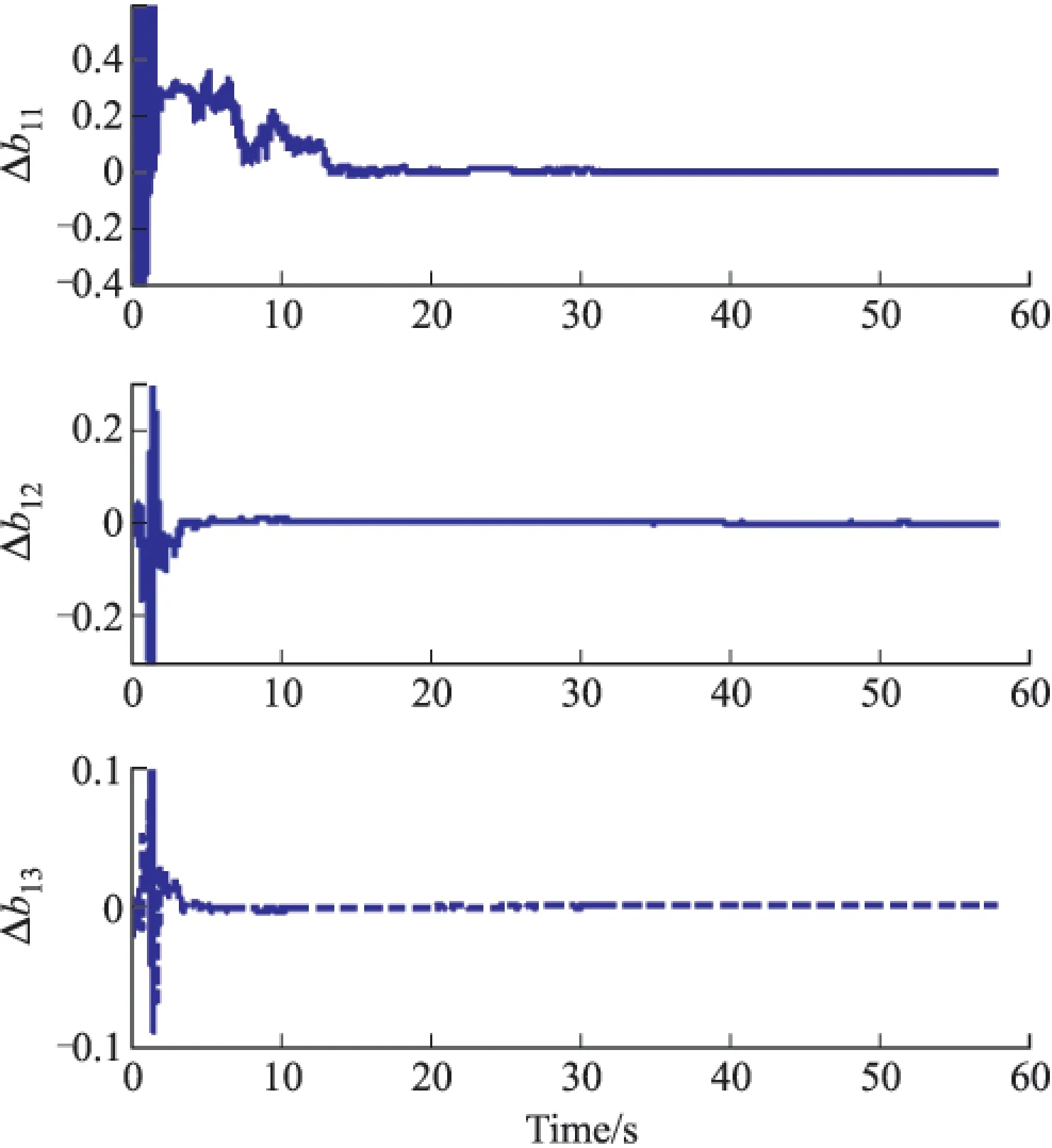
图6 涡流磁化系数b1j(j=1,2,3)误差收敛曲线
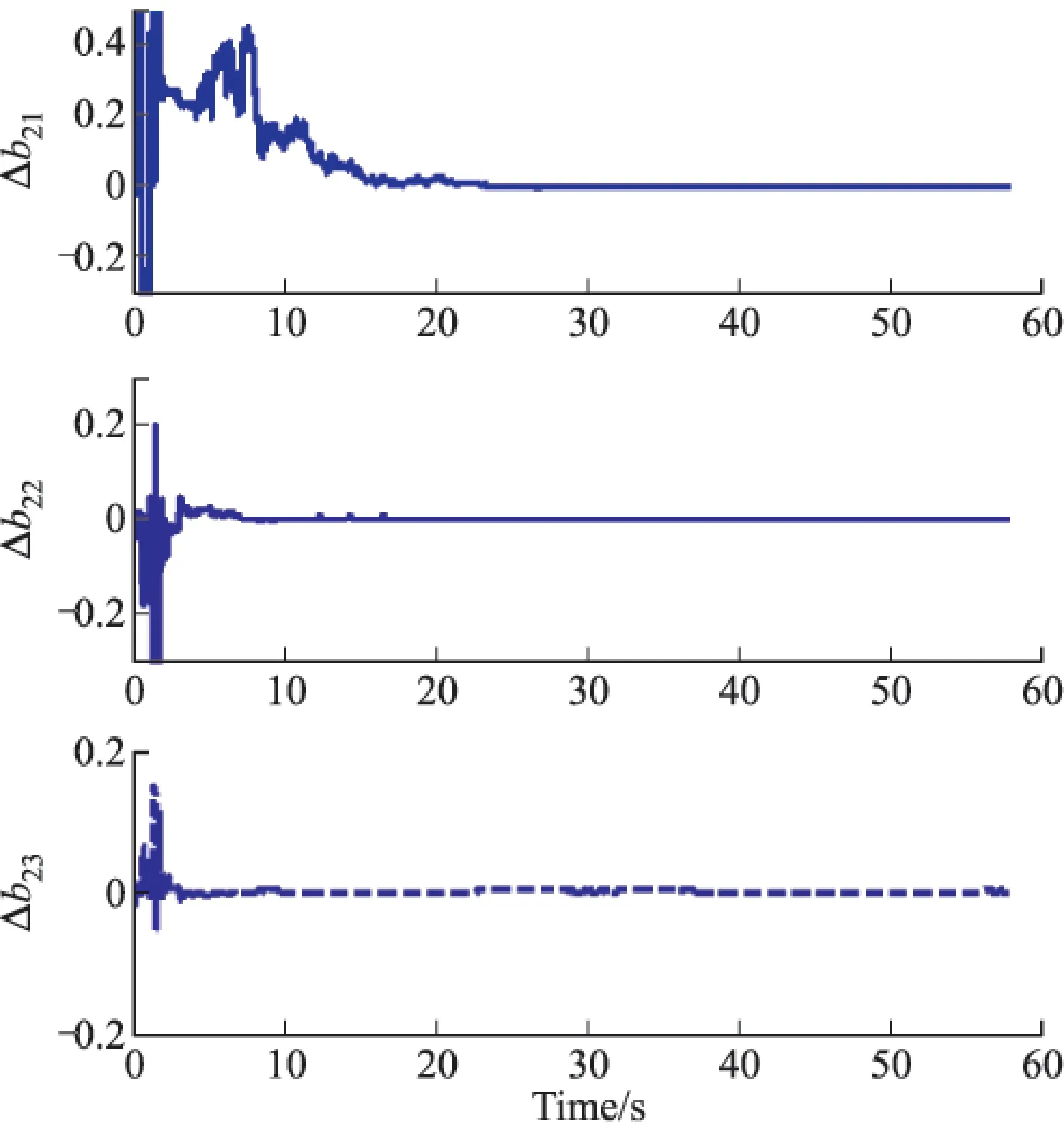
图7 涡流磁化系数b2j(j=1,2,3)误差收敛曲线

图8 涡流磁化系数b3j(j=1,2,3)误差收敛曲线
1)干扰磁场误差参数滤波结果
从图2~图8所示的滤波结果来看,包括固定磁场、软磁感应和涡流磁化系数在内的所有干扰磁场误差参数均能够很好的收敛。其中,图2所示固定磁场估计误差方差分别为2.915 2nT、8.975 3nT和6.924 8nT;而图3~图5所示为载体软磁磁化系数估计结果,从结果来看,其软磁磁化系数在10s内都能够收敛,滤波器具有快的收敛速度和高的滤波估计精度;相对而言,软磁磁化系数中的c13、c23和c33滤波估计误差相对较大。
2)载体干扰磁场补偿结果对比
算法在进行上述误差参数滤波估计的同时进行磁测数据补偿,地磁传感器补偿前后对比如图9~图11所示。

图9 X轴地磁传感器补偿前后对比
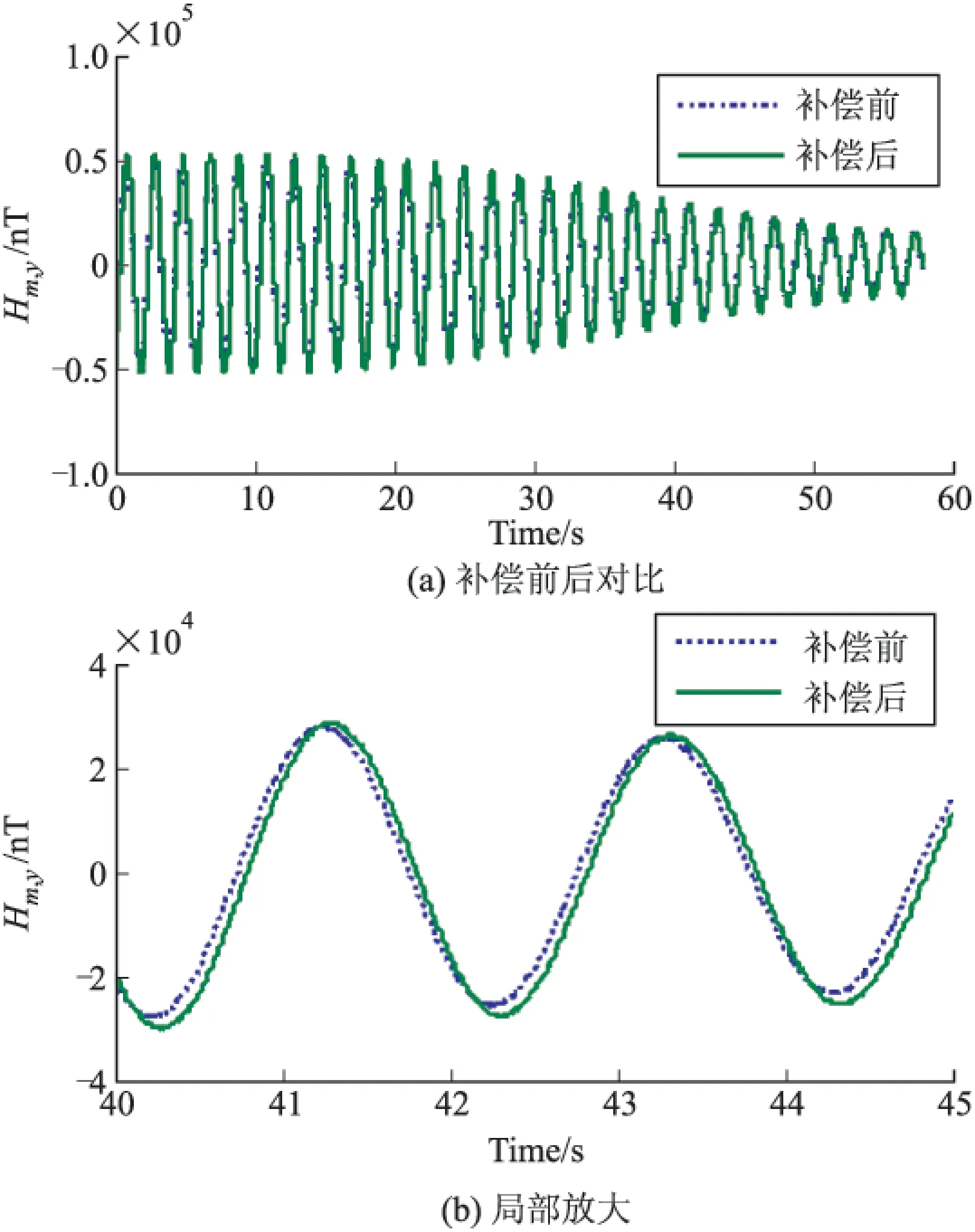
图10 Y轴地磁传感器补偿前后对比

图11 Z轴地磁传感器补偿前后对比
为便于观察,图9~图11所示各图中下半部分为
40~45s内的局部放大图。从上述仿真结果来看,X、Y和Z轴向地磁测量误差在进行误差补偿后,其测量精度明显得到提高,各轴向地磁传感器的测量误差均值小于60nT。
图12所示为地磁场总场强度在补偿前后结果对比,其中,补偿前的误差均值为8767.9nT、标准差为3147.3nT, 而补偿后其误差均值减小为0.79nT、方
差为225.6nT,地磁传感器的测量精度提高了一个数量级。
4结论
针对地磁导航中高速旋转弹载体磁场干扰影响磁测精度的问题,文中首先推导了载体干扰磁场数学模型,然后基于所建立的载体磁场模型,提出了磁场干扰误差参数估计与磁测数据的补偿方法,并采用Kalman滤波算法设计了误差参数估计滤波器。最后以152mm旋转弹药载体磁场为研究仿真对象,利用计算机仿真方法进行了所述算法的仿真分析。仿真结果表明,载体磁场滤波器能有效完成包括弹体固定磁场、软磁感应和涡流磁化在内的干扰磁场误差系数的准确估计,而且地磁传感器在经过磁测数据补偿后,其测量精度提高了一个数量级。
参考文献:
[1]李季, 张琦, 潘孟春, 等. 载体干扰磁场补偿方法 [J]. 国防科技大学学报, 2013, 35(3): 7-11.
[2]张晓明, 赵剡. 基于椭圆约束的新型载体磁场标定及补偿技术 [J]. 仪器仪表学报, 2009, 30(11): 2438-2443.
[3]GOLDENBERGF.Geomagneticnavigationbeyondthemagneticcompass[C]∥ProceedingsoftheInternationalSymposiumonPosition,LocationandNavigation, 2006: 684-694.
[4]于振涛, 吕俊伟, 稽绍康. 基于椭球约束的载体三维磁场补偿方法 [J]. 哈尔滨工程大学学报, 2014, 35(6): 731-734.
[5]寇义民, 夏红伟, 刘睿, 等. 一种地磁导航中的低频电磁干扰场分离方法 [J]. 哈尔滨工业大学学报, 2011, 43(7): 32-37.
[6]刘仁浩, 王华. 数字磁罗盘的全姿态罗差补偿 [J]. 光学精密工程, 2011, 19(8): 1867-1873.
[7]邱丹, 黄圣国. 组合航向系统中数字磁罗盘的罗差补偿研究 [J]. 仪器仪表学报, 2006, 27(S2): 1369-1371.
[8]李永慧, 张晓明, 陈国彬, 等. 某常规弹载体感应磁场分布的仿真技术研究 [J]. 弹箭与制导学报, 2012, 32(3): 569-571.
[9]LELIAKP.Identificationandevaluationofmagnetic-fieldsourcesofmagneticairbornedetectorequippedaircraft[J].IRETransactionsonAerospaelandNavigationalElectronics, 1961,ANI-8(3): 95-105.
[10]龙达峰, 温晶晶, 张晓明. 高速旋转弹捷联磁传感器在线校准方法 [J]. 弹箭与制导学报, 2014, 32(4): 181-183.
[11]HEPNERDAVIDJ,HARKINSTHOMASE.Determininginertialorientationofaspinningbodywithbody-fixedsensors[C]∥Proc.SPIE4025onAcquisition,Tracking,andPointing, 2000: 68-78.
[12]向超. 旋转弹体背景磁场模型和地磁姿态测试方法研究 [D]. 北京: 南京理工大学, 2013.
[13]秦永元. 惯性导航 [M]. 北京: 科学出版社, 2005: 327-330.
*收稿日期:2015-03-06
基金项目:国家自然科学基金(51375463)资助
作者简介:龙达峰(1979-),男,广东梅州人,讲师,博士研究生,研究方向:地磁导航技术。
中图分类号:TJ410.6
文献标志码:A
CompensationAlgorithmofInterferentialMagneticFieldforHigh-spinProjectiles
LONGDafeng1,LIUJun1,2,ZHANGXiaoming1,LIJie1
(1NationalKeyLaboratoryforElectronicMeasurementTechnology,NorthUniversityofChina,Taiyuan030051,China;2KeyLaboratoryofInstrumentationScience&DynamicMeasurement(NorthUniversityofChina),MinistryofEducation,Taiyuan030051,China)
Abstract:Vehicle interferential magnetic field is a main factor affecting measurement of magnetometer in geomagnetic navigation. In this paper, a vehicle’s magnetic field compensation algorithm was presented, generation mechanism of vehicle’s magnetic field distribution was analyzed, and compensation model was rebuilt. Finally, the 152 mm spin-projectile was selected as the research object, and the method of magnetic field compensation was simulated and analyzed. Simulations demonstrate that the estimator can effectively estimate error parameters of magnetic interference. Moreover, online compensation significantly enhances performance of magnetometer.
Keywords:magnetometer; flight vehicle interferential magnetic field; compensation algorithm; high-spin projectiles

