杀爆战斗部破片与冲击波运动规律研究*
龚超安,陈智刚,印立魁
(中北大学地下目标毁伤技术国防重点学科实验室,太原 030051)
杀爆战斗部破片与冲击波运动规律研究*
龚超安,陈智刚,印立魁
(中北大学地下目标毁伤技术国防重点学科实验室,太原030051)
摘要:通过对杀爆战斗部爆炸后破片运动及冲击波传播的研究,为提高破片和冲击波相遇位置的计算精度,理论推导了新的计算方法。采用Visual C++开发破片与冲击波运动规律计算系统使计算方便。运用ANSYS/LS-DYNA数值模拟了某预制破片战斗部爆炸后破片与冲击波的运动,数值模拟与该模型计算结果相符,较以往计算模型精度提高了8.3%。
关键词:破片;冲击波;运动规律;LS-DYNA
0引言
杀爆战斗部作为反导战斗部主要采用的方式,国内外对其研究从未中断过。杀爆战斗部对目标主要有三个破坏作用:爆轰生成物的直接作用、冲击波的破坏作用以及破片的杀伤作用。其中就冲击波和破片对目标的作用研究较多。作为两种毁伤元,其对目标的作用原理不同导致作用顺序影响毁伤效能[1-2]。因此,破片与冲击波相遇位置计算的研究极其重要。文献[3]根据试验数据对不同比例距离、装填系数和破片与冲击波相遇时间进行拟合。冲击波传播距离与时间的关系目前没有准确的表达式,任意时刻破片与冲击波的距离及位置未有精确计算。
1TNT当量转换计算
1.1带壳装药等效为裸露装药
带壳炸药爆炸时,根据能量守恒定律,质量为m的炸药释放出的总能量用于爆炸产物的内能和动能的增加,以及破片飞散的动能,即[4]:
mQv=E1+E2+E3
(1)
E1+E2=mQv-E3=mbeQv
带壳装药等效裸露装药的当量计算,令β=m/M为装填系数,对于圆柱形壳体装药:
(2)
1.2其他炸药等效TNT球形装药
其他类型的炸药在无限空气介质中爆炸转换为TNT,设某一炸药的爆热是Qvi,药量是mbe,其TNT当量为ω=mbeQvi/QvT,式中QvT为TNT的爆热。杀爆弹大部分装药为圆柱形,冲击波传播距离大于装药特征尺寸,可近似看成球形装药的爆炸。
2冲击波速度
2.1TNT超压计算
对于裸露的TNT球形装药在无限空气中爆炸,正压区峰值超压为ΔP+,我国国防工程设计规范中规定的计算公式为[4]:
(3)

2.2冲击波超压与冲击波速度关系
表征冲击波超压与速度关系的兰金-雨果尼奥(Rankine-Hugoniot)方程[5]为:
(4)
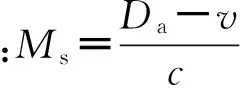
(5)
对上式倒数积分即是时间t与距爆心的距离R的关系。
(6)
由于式(6)解析解非常复杂,给计算带来困难,文献[6,8]用拟合式(7)近似代替计算,但此式使用范围有限,且对装填比大于1的模型误差较大。
(7)
在实际计算中,可将式(6)转化为数值积分。采用划分区间指定步长,反复积出一系列的点,并绘制成曲线。点的密集度直接反应计算的精度,并由步长体现。式(6)、式(7)与文献[9]试验结果对比如图1所示。
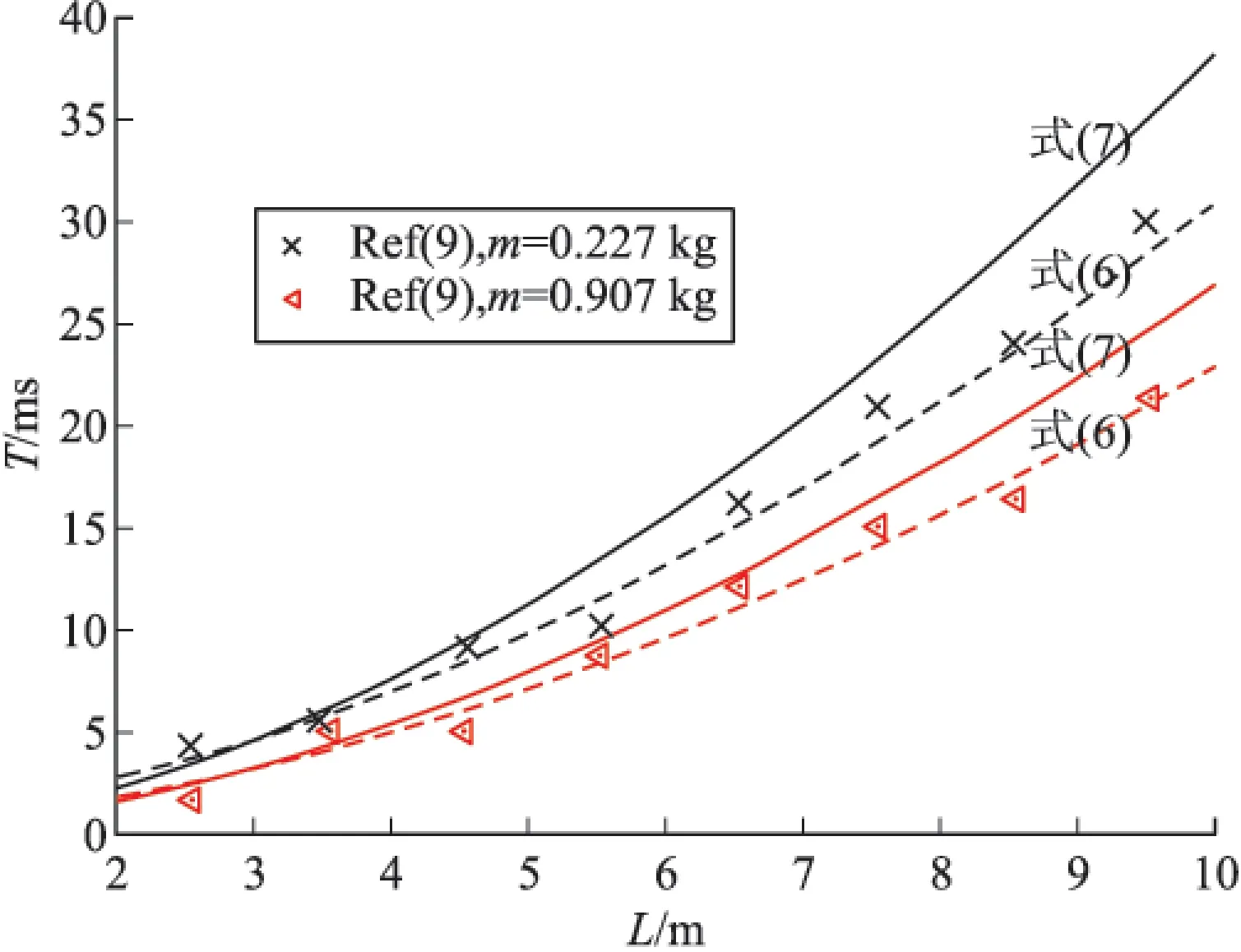
图1 式(6)、式(7)计算值与试验值比较
3破片初速及衰减
3.1破片初速
由能量守恒定律和Gurney假设得到的计算破片初速的Gurney公式[4]:
(8)


表1 破片初速修正系数及衰减系数
3.2破片速度衰减

(9)
此关系式按照理论表征破片飞行距离与时间的关系,且对各种破片分别进行计算,比文献[7-8]采用的近似式(10)适用范围广,且在考虑大气压力改变的情况下比式(10)精确。
(10)
4破片与冲击波计算系统
要求破片与冲击波相遇位置,鉴于理论的真实性和计算的方便性,采用Visual C++开发破片与冲击波位移时间计算系统。数据处理及界面由MFC控制,坐标系绘图用TeeChart控件完成。该计算系统框架结构流程如图2所示。
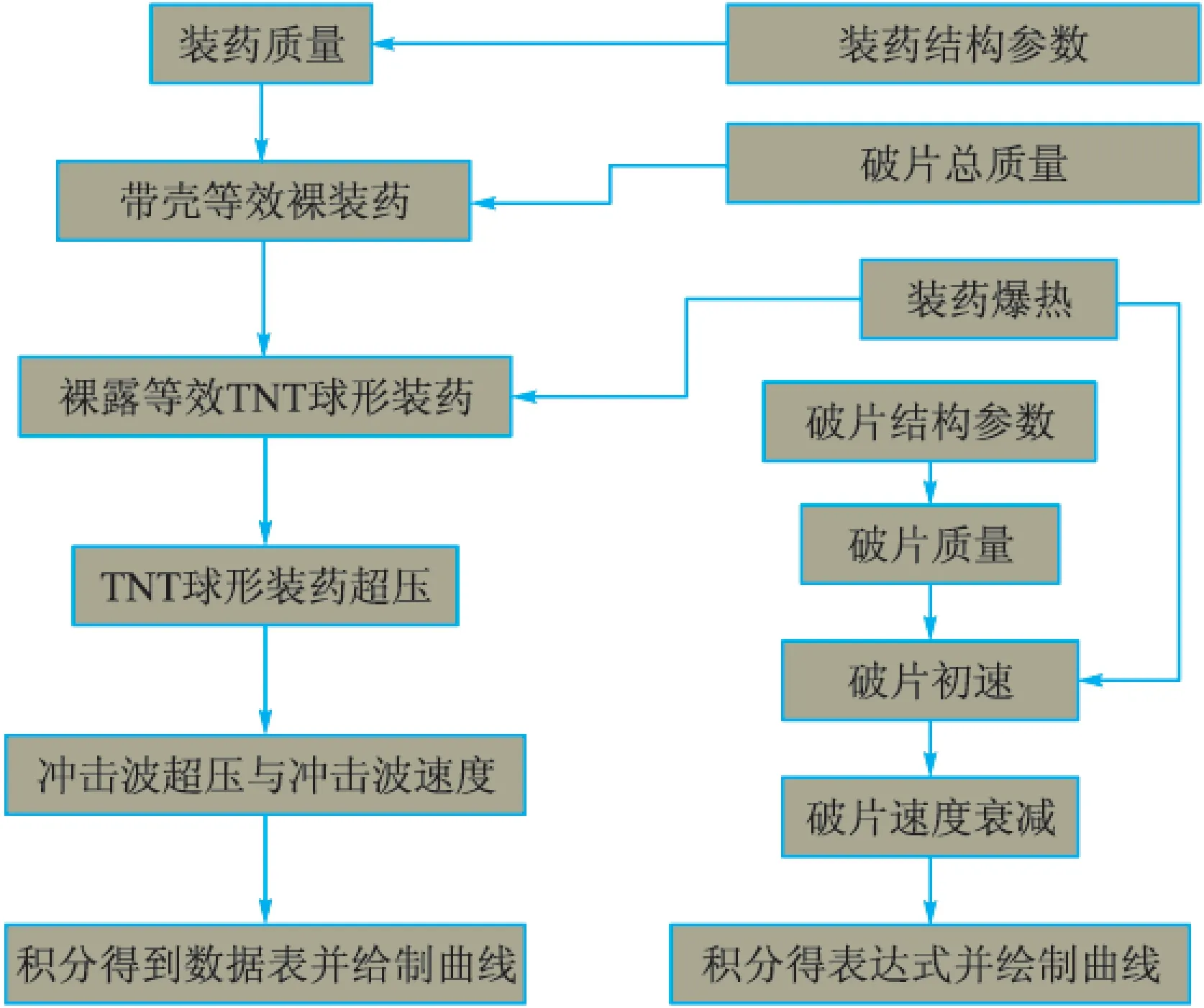
图2 破片与冲击波计算系统结构
5实例分析
某杀爆战斗部TNT圆柱形装药半径为4.8 cm,药柱高50 cm,单个预制方块钢破片质量为0.04 kg,破片沿轴向22层,每层42个,总破片质量为37 kg。
5.1按照以往计算方法
1)破片初速计算
2)飞行距离为L的飞行时间
3)等效TNT当量
1.502kg
4)冲击波传播至L处的时间ta
5)冲击波与破片相遇
令T=ta得出L=4.30m
5.2文中方法
将各参数代入计算系统如图3。
生成曲线见图4,起爆后破片与冲击波的运动分为两个阶段,第一阶段:开始冲击波速度大于破片速度,冲击波在前,破片在后;第二阶段:冲击波速度衰减比破片速度衰减快,破片与冲击波相遇后,破片在前冲击波在后。破片在前期速度衰减较小,与冲击波在7.1ms时刻相遇于距爆心4.73m处。
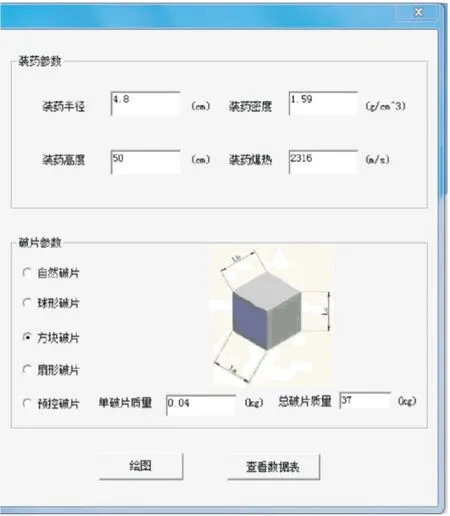
图3 各参数输入窗口

图4 破片与冲击波运动时间位移曲线
5.3破片与冲击波相遇数值模拟
文中运用ANSYS-LSDYNA软件对装药爆炸驱动破片运动进行仿真。由于结构对称,采用1/4建模简化计算,炸药和空气采用多物质ALE体单元,破片采用Lagrange体单元,ALE体单元和Lagrange体单元之间进行流-固耦合。建7m半径的空气域,冲击波由空气域内压力体现。装药TNT密度为1.63g/cm3,其本构关系的描述选用MAT_HIGH_EXPLOSIVE_BURN形式,状态方程采用JWL状态方程,起爆方式为点起爆;钢破片密度7.83g/cm3,本构方程选用Johnson-Cook模型,状态方程为Gruneisen方程。仿真结果的为压力云图(见图5),压力峰值处为冲击波位置,破片也运动到该位置,在7ms时刻破片与冲击波于4.96m处相遇。

图5 7 ms时刻破片与冲击波相遇

破片类型相遇位置/m原方法文中方法仿真结果偏差/%方块4.304.734.698.3%
表2对3种方法的结果进行对比,以数值模拟为准,原方法偏差为8.3%,文中计算方法与数值模拟结果相接近。对于预制破片,部分爆轰产物从预制破片间隙穿过,对冲击波有加强作用,使冲击波在第一阶段的位移增加,相遇距离变大。
6结语
1)此计算全过程皆有理论依据,适用于所有模型,提高了计算精度。并将预制破片与自然破片用初速修正系数分开计算,避免了按照以往计算结果相同。
2)曲线中任意时刻破片与冲击波的距离都可读出,破片与冲击波运动的两个阶段特点都反映在曲线中,更能准确控制破片与冲击波对目标的作用顺序及距离。
参考文献:
[1]董秋阳. 机翼蒙皮在破片和冲击波作用下的损伤研究 [D]. 南京: 南京航空航天大学, 2013.
[2]任丹萍. 破片和冲击波复合作用下对导弹的毁伤 [D]. 南京: 南京理工大学, 2006.
[3]刘水江. 复合防破片板防护性能分析及数值模拟 [D]. 武汉: 武汉理工大学, 2007.
[4]隋树元, 王树山. 终点效应学 [M]. 北京: 国防工业出版社, 2000: 290-292.
[5]张宝平, 张庆明, 黄风雷. 爆轰物理学 [M]. 北京: 兵器工业出版社, 2009: 54-57.
[6]STARKSMW.Vulnerabilityscience,aresponsetoacriticismoftheballisticresearchhaboratoey’svulnerabilitymodelingstrategy:AD-A224785 [R].ArmyBallisticResearchLab, 1990.
[7]曾首义, 蒋志刚, 陈斌, 等. 冲击波与破片共同作用探讨 [C]∥中国土木工程学会防护工程分会第九次学术年会论文集, 2004: 263-367.
[8]梁为民, 张晓忠, 梁任发, 等. 结构内爆炸破片与冲击波运动规律试验研究 [J]. 兵工学报, 2009, 30(S2): 289-292.
[9]NorrisJHuffington,WilliamOEwing.Reflectedimpulsenearsphericalcharges:AD-A160 797 [R].ArmyBallisticResearchLab, 1985.
*收稿日期:2015-04-16
作者简介:龚超安(1990-),男,四川仪陇人,硕士研究生,研究方向:弹箭控制与高效毁伤。
中图分类号:TJ410
文献标志码:A
Research on Motion Law of Fragment and Shock Wave of Blast Fragmentation Warhead
GONG Chaoan,CHEN Zhigang,YIN Likui
(National Defense Key Subject Laboratory of Underground Target Damage Technology, North University of China, Taiyuan 030051, China)
Abstract:According to study of shock wave propagation and fragment movement after explosion of blast fragmentation warhead, a more accurate way was provided for calculation of fragments and shock wave propagation distance and the time delayed. A computing system of fragments and shock wave’s movement was developed by using Visual C++. It makes calculation be more convenient. Movement of preformed fragments and shock wave after explosion was simulated. The results show that the simulation tally with the new calculation model and the accuracy is improved by 8.3%.
Keywords:fragment; shock wave; motion law; LS-DYNA

