基于G-MPSP算法的非线性制导律研究*
李新三,汪立新,丁邦平,闫循良,刘国辉,王明建
(1 第二炮兵工程大学,西安 710025;2 第二炮兵工程大学士官职业技术教育学院,山东青州 262500)
基于G-MPSP算法的非线性制导律研究*
李新三1,汪立新1,丁邦平2,闫循良1,刘国辉2,王明建2
(1第二炮兵工程大学,西安710025;2第二炮兵工程大学士官职业技术教育学院,山东青州262500)
摘要:针对带有末端多约束的非线性制导问题,运用通用模型预测静态规划(G-MPSP)算法设计了一种快速求解连续时间系统具有终端落角约束的非线性最优制导律。该算法通过向后迭代求解小维数权矩阵微分方程对控制量进行更新,将动态优化问题转化为静态优化问题,计算效率得以提高。考虑目标以不同的方式机动,仿真结果表明,末端位移偏差小于1.0 m,末端角度约束偏差可控制在0.1°范围内,该制导律能够满足脱靶量和末端角度双重要求,法向过载在整个制导过程中变化平缓。
关键词:制导律;角度约束;模型预测静态规划
0引言
运用最优控制理论设计对地攻击导弹制导律具有许多优点,不仅可以考虑多种约束条件,同时还可以对给定的目标函数进行优化[1],例如梯度法[2]、打靶法[3]等。但是这些传统的优化算法计算量大,只适用于离线轨迹优化。LQR理论[4]通过求解代数黎卡提方程来获得最优控制量,但是LQR理论仅仅适用于线性时不变系统。目前,非线性最优控制理论在导弹上在线应用主要分为两类方法:1)参考轨迹跟踪法;2)预测-校正法。参考轨迹跟踪法需要离线生成参考轨迹。预测-校正法首先利用猜测的初始控制量对末端状态进行预测,然后利用末端状态实际值与期望值的偏差对控制量进行更新。伪谱法[5-6]是一种在计算效率方面有很好效果的预测-校正法,但是该方法需要谨慎选择基底函数和配置极点。
借鉴模型预测控制方法(MPC)[4]思想,文中给出一种通用模型预测静态规划算法(G-MPSP)来快速求解具有末端约束的非线性制导问题。G-MPSP算法将动态规划问题转化为静态规划问题,拉格朗日乘子以显式表达式形式给出。该算法受近几年研究比较热的MPSP[7-10]算法启发很大,在欧拉积分条件下,两种算法相互等价,在文中将加以证明。仿真验证表明该制导方法能够满足末端角度和脱靶量的双重要求,法向过载变化平缓,末端时刻不会突变。
1G-MPSP制导算法
采用如下形式的非线性系统状态方程和输出方程如下:

式中:X∈Rn为状态量,U∈Rm为控制量,Y∈Rp为输出量。文中给出的制导算法需要确定初始控制量,通过优化的方法实现对当前控制量U(t)的更新,确保末端时刻输出量Yd(tf)满足:Y(tf)→Yd(tf)。
末端时刻tf对应的输出量偏差可表示为:
(3)
G-MPSP制导算法通过对控制量进行更新确保末端时刻输出量偏差δY(X(tf))→0。下面将对G-MPSP制导算法进行推导。
式(1)等号两边与权矩阵W(t)相乘,得:
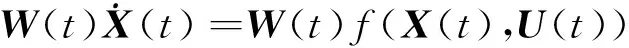
(4)
式中:W(t)∈Rp×n,可以通过W(t)将系统状态方程映射到输出空间,减小系统动力学方程的维数,可以缩短运算时间。
式(4)进行积分运算,得:
(5)
Y(X(tf))加到式(5)左右两边,得:
(6)
对式(6)最后一项进行分步积分,得:
(7)
将式(7)代入式(6)得:

(8)
上式进行变分运算,得:
(9)
式(9)中,选取合适的W(t)可以使与δX(t)相关的系数项为零,得:
(10)
(11)
式(10)和式(11)为关于W(t)的微分方程和边界条件,对式(10)反向积分运算可以求解W(t)。
对于确定的初始条件,δX(t0)=0。结合式(10)和式(9),得:
(12)
式中:
(13)
其中,Bs(t)为控制量偏差δU(t)和输出量偏差δY(X(tf))之间的灵敏矩阵,即式(12)建立了末端时刻tf对应的输出量偏差和t∈[t0,tf)时间历程内的控制量偏差之间的联系。
性能指标函数如下式:
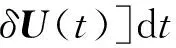
(14)
式中:Up(t)代表更新前的控制量;δU(t)为控制量偏差。将末端约束考虑进去,式(14)可以表示为:
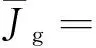
(15)
式中:λ∈Rp为静态拉格朗日乘子。式(15)进行变分运算,得:
(16)
t=tf
(17)
由式(16)得:
(18)
将式(18)代入式(17),得:
(19)
其中:
(20)
(21)
当Aλ非奇异时,由式(19)得:
(22)
式(22)可以求得静态变量拉格朗日乘子λ。文中给出的制导算法避免求解时变协态变量的问题,简化了计算。
将式(22)代入式(18),得:
(23)
由式(23)可得到更新后的控制量:
(24)
文中给出的制导算法通过将动态优化问题转化为维数更小的静态优化问题进行求解,只需要求解静态拉格朗日乘子,这种处理方法使得优化问题的求解更简单。
基于欧拉近似处理,G-MPSP算法与MPSP算法是相互等价的[11]。与MPSP相比,G-MPSP不需要对运动方程进行离散化处理。由于论文篇幅的限制,文中不予证明。
2基于G-MPSP的制导律设计
图1为导弹与目标运动示意图,M为导弹,T为目标,导弹的速度为Vm,弹道倾角为γm,弹道偏角为ψm,导弹的位移分别为xm、ym、zm,导弹法向过载指令分别为az、ay,下标f代表末端时刻导弹状态量。假设目标低速机动,要求导弹精确击中目标,弹道偏角和倾角满足ψm(tf)→ψmf,γm(tf)→γmf约束。

图1 导弹目标运动示意图
状态方程经归一化处理得:
(25)
其中:Xn=[Vmnγmnψmnxmnymnzmn]T为归一化处理后的状态量;Un=[aznayn]T为归一化处理后的控制量;Tm为推力;Dm为阻力。
选择输出量:
(26)
式(25)对状态量微分,得:
(27)
式(25)对控制量微分,得:
(28)
式(26)对末端时刻状态量Xn(tf)微分,得:
(29)
G-MPSP算法制导律设计时,需要对初始控制量进行猜测,文中运用增广比例制导对初始控制量进行猜测。文献[12]推导出的增广比例制导(APN)方向加速度指令为:
(30)
(31)
G-MPSP制导律设计执行流程如下:
1)选择初始控制量,文中通过增广比例导引律(APN)计算初始控制量,这一步将给出导弹的飞行时间tf[11]。
(2)求末端时刻输出量偏差δY(tf)=Yd(tf)-Y(tf),Yd(tf)由目标状态和给定的导弹期望角度约束确定,如果偏差值满足设计要求,程序结束;如果不满足要求,执行步骤3)。
3)对式(10)和式(11)进行数值积分计算W(t),文中采用四阶龙格库塔方法。
4)由式(13)计算Bs(t)。
5)由式(20)和式(21)计算Aλ和bλ。
6)最后,由式(23)和式(24)计算δU(t)和U(t),令Up(t)=U(t),回到步骤1)进行下一步迭代。
3数值仿真
仿真时考虑攻击地面机动目标。导弹质量:t≤6 s时,mm=165 kg;t>6 s时,mm=150 kg。导弹推力:t≤6 s时,Tm=5 880 N;t>6 s时,Tm=0 N。导弹参考面积Sm=0.032 4 m2。阻力Dm计算参考文献[12]。导弹初始速度为635 m/s,初始位置为(10 000 m,5 000 m,5 000 m),初始弹道倾角和偏角为(0°,170°),末端时刻弹道倾角和偏角期望值为(-60°,250°)。目标速度为20 m/s,初始位置为(1 000 m,0 m),初始航迹偏角为60°。归一化速度、角度、位移和加速度分别取为600 m/s、50°、5000 m和9.81 m/s2,APN系数Ne=3,仿真步长取为0.02 s。
仿真时分别考虑目标的3种机动方式:正弦机动,常值加速度机动和零值加速度机动。正弦机动时目标加速度为ayT=2gsin(ωt),机动频率w=1 rad/s;常值加速度机动时目标加速度ayT=g;零值加速度机动目标加速度ayT=0,ψT为常值。

图2 不同机动方式下的三维轨迹图
仿真时经过6次迭代即可满足迭代终止条件。图2给出了目标以不同的方式机动时,导弹飞行的三维轨迹,图3给出了导弹击中目标时三维轨迹放大图。图4和图5给出了目标以不同的方式机动导弹飞行时弹道倾角γm和偏角ψm的变化曲线。表1给出了末端时刻导弹和目标的输出参数,由仿真结果可知,末端时刻导弹飞行的弹道倾角γmf和偏角ψmf与给定的期望约束值之间的偏差在0.1°范围内,位移参数(xmf,ymf,zmf)的偏差在1 m范围内,即文中所提出的G-MPSP算法能较好的满足末端约束要求。

图3 击中目标时轨迹放大图
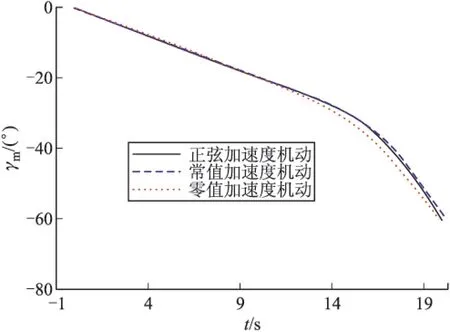
图4 弹道倾角γm变化曲线
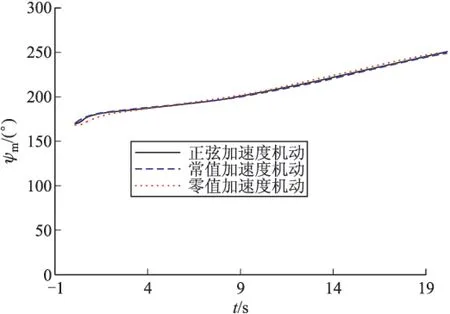
图5 导弹偏角ψm变化曲线
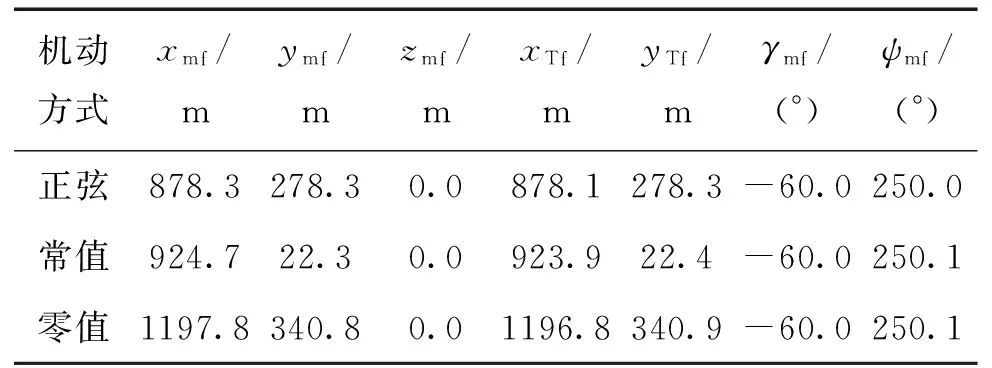
机动方式xmf/mymf/mzmf/mxTf/myTf/mγmf/(°)ψmf/(°)正弦878.3278.30.0878.1278.3-60.0250.0常值924.722.30.0923.922.4-60.0250.1零值1197.8340.80.01196.8340.9-60.0250.1
图6和图7为目标机动时,法向过载az和ay的变化曲线。与传统的PN制导律相比,G-MPSP算法攻击机动目标时终端时刻法向过载az和ay不会突变;在制导过程中,法向过载az和ay大小变化比较平缓。
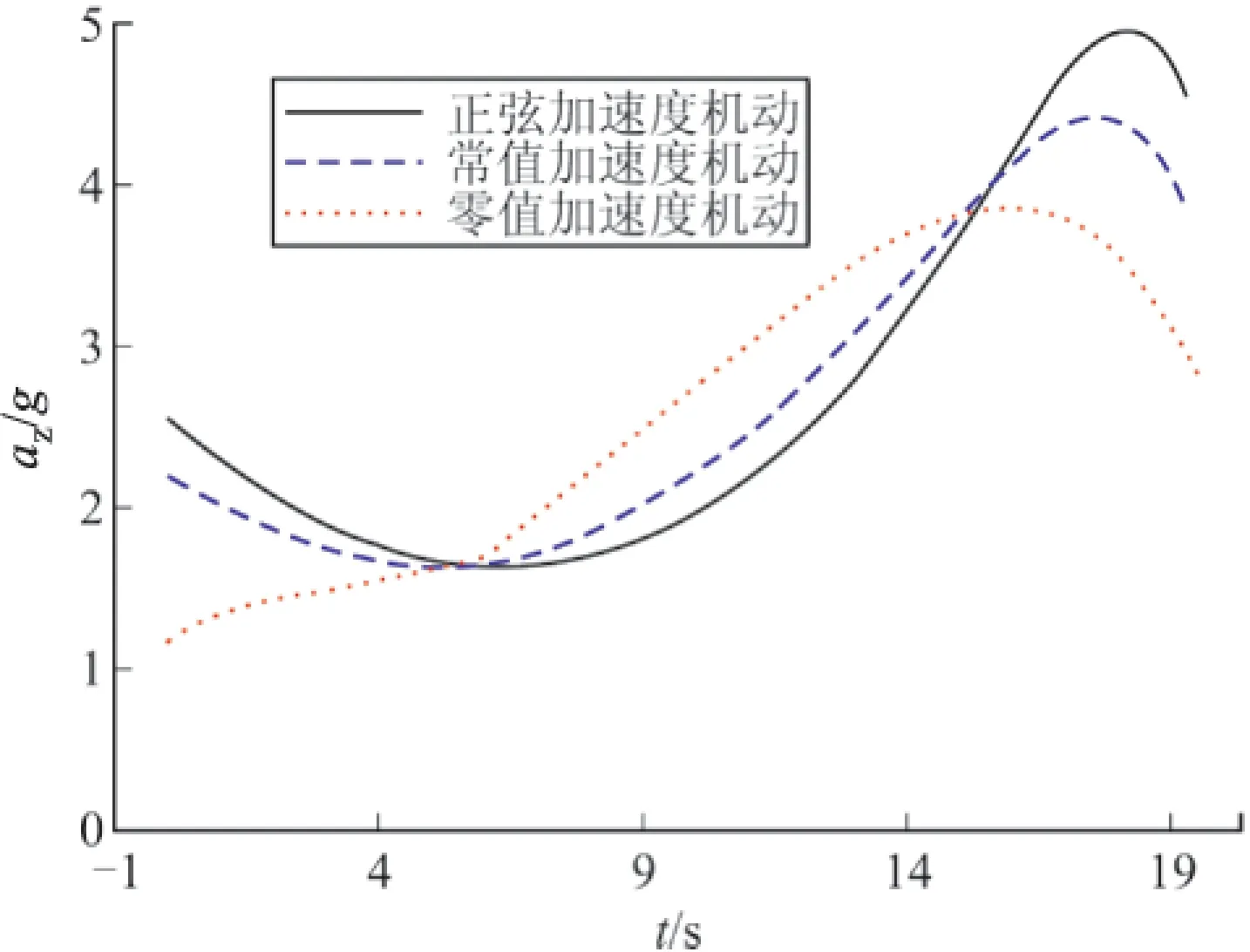
图6 法向过载az变化曲线
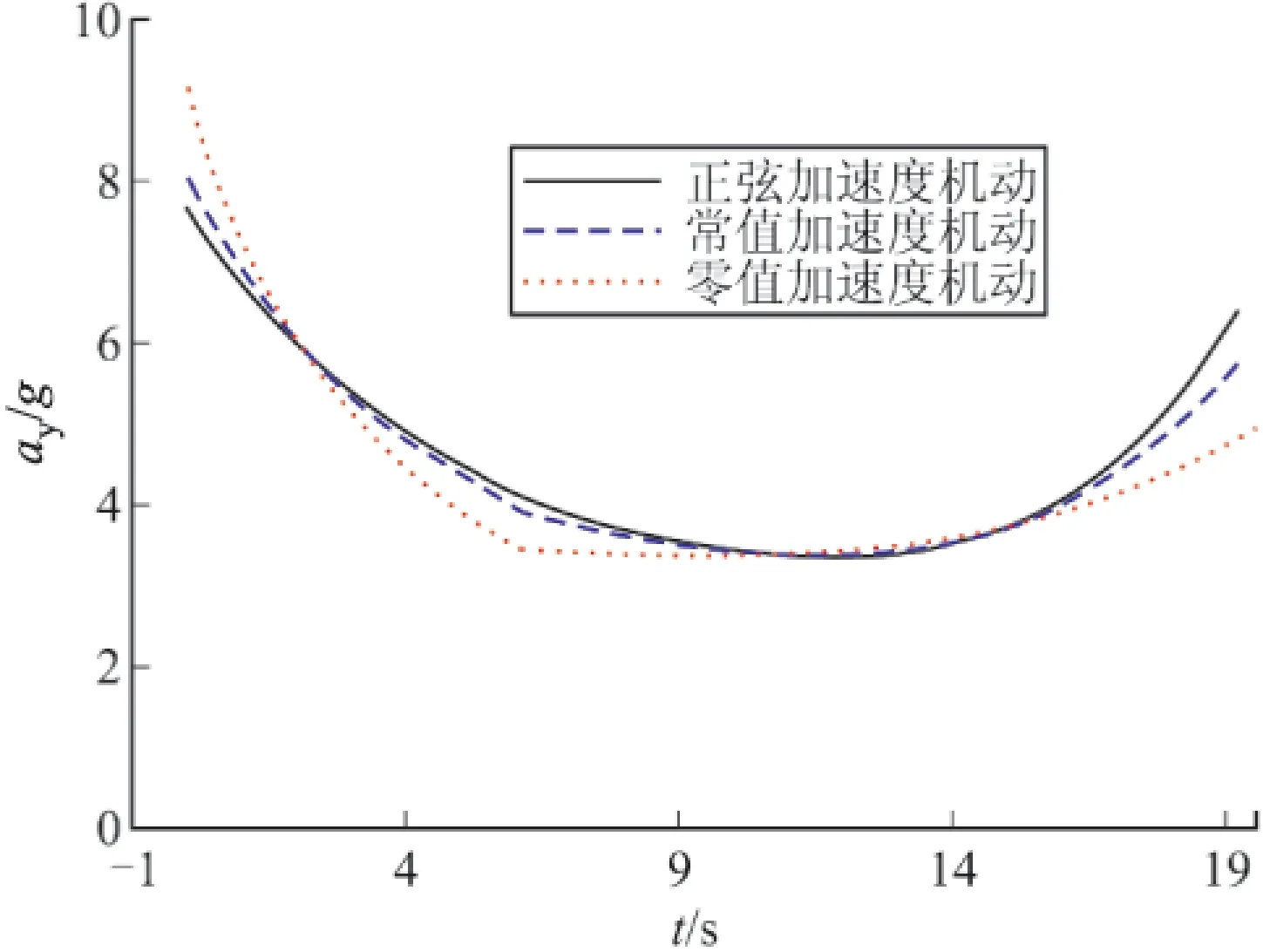
图7 法向过载ay变化曲线
4结论
文中针对带有末端角度约束的机动目标非线性制导问题,设计了一种通用模型预测静态规划(G-MPSP)制导算法,推导了算法的制导原理。该算法避免了求解时变协态变量,具有在线应用的潜力。设计数值仿真验证了该算法的有效性。下一步将考虑不同的初始控制量猜测方法对G-MPSP算法执行效率的影响,并验证G-MPSP算法的实时性。
参考文献:
[1]BRYSON J A E, HO Y C. Applied optimal control [M]. New York: John Wiley & Sons, 1975.
[2]ROBERTS S M, SHIPMAN J S. Two-point boundary value
problems: Shooting methods [M]. New York: American Elsevier Publishing Company Inc, 1972.
[3]KIRK D E. Optimal control theory: an introduction [M]. NewJersey, USA: Prentice Hal, 1970.
[4]BETTS J T. Practical methods for optimal control using nonlinear programming [M]. Philadelphia: Society for Industrial and Applied Mathematics, 2001: 61-125.
[5]GONG Q, KANG W, ROSS I M. A pseudospectral method for the optimal control of constrained feedback linearizable systems [J]. IEEE Transactions on Automatic Control, 2006, 51(7): 1115-1129.
[6]GONG Q, FAHROO F, ROSS I M. Spectral algorithm for pseudospectral methods in optimal control [J]. Journal of Guidance, Control, and Dynamics, 2008, 31(3): 460-471.
[7]ROSSITER J A. Model based predictive control: A practical approach[R]. New York: CRC, 2003.
[8]PADHI R, KOTHARI M. Model predictive static programming: A computationally efficient technique for suboptimal control design [J]. International Journal of Innovative Computing, Information and Control, 2009, 5(2): 399-411.
[9]OZA H B, PADHI R. Impact-angle-constrained suboptimal model predictive static programming guidance of air-to-ground missiles [J]. Journal of Guidance, Control, and Dynamics, 2012, 35(1): 153-164.
[10]郭鹏飞, 佘浩平. 一种具有落角约束的非线性次优制导律[C]∥第32届中国控制工程会议, 2013.
[11]MAITY Arnab, OZA Harshal B, Radhakant Padhi. Generalized model predictive static programming and its application to 3D impact angle constrained guidance of air-to-surface missiles[C]∥ 2013 American Control Conference (ACC), 2013.
[12]IMADO F, KURODA T, TAHK M J. A new missile guidance algorithm against a maneuvering target[C]∥ Proceedings of the AIAA Guidance, Navigation, and Control Conference and Exhibit, 1998.
*收稿日期:2015-01-12
基金项目:国家自然科学基金(61203354)资助
作者简介:李新三(1982-),男,湖北广水人,讲师,博士,研究方向:飞行器制导与控制技术。
中图分类号:V444
文献标志码:A
Nonlinear Guidance Law Research Based on G-MPSP Technique
LI Xinsan1,WANG Lixin1,DING Bangping2,YAN Xunliang1,LIU Guohui2,WANG Mingjian2
(1The Second Artillery Engineering University, Xi’an 710025, China; 2College of Sergeant Occupation Technology Education,The Second Artillery Engineering University, Shandong Qingzhou 262500, China)
Abstract:Generalized model predictive static programming (G-MPSP) technique was presented in this paper in continuous time framework for rapidly solving a class of nonlinear optimal control problems with hard multiple terminal constraints. A key feature of the technique is backward propagation of a small-dimensional weight matrix dynamics, using which the control history got updated. It leads to a static optimization problem and it is the reason for its high computational efficiency. Different maneuvering ground targets were considered in the simulation studies. Simulation results show that final miss distance is less than 1.0 m, terminal impact angle errors are less than 0.1°. Impact angle constraints are met in addition to achieving near zero miss distance and the variation in the lateral acceleration history is quite smooth throughout the engagement.
Keywords:guidance law; impact angle constraints; model predictive static programming

